
Functions of several variables- Textbook..pdf
.pdf
MINISTRY OF EDUCATION AND SCIENCE YOUTH AND SPORTS OF UKRAINE
ODESSA NATIONAL A.S.POPOV ACADEMY OF TELECOMMUNICATIONS
Department of Higher Mathematics
Gavdzinski V.N., Korobova L.N., Maltseva E.V.
FUNCTIONS OF SEVERAL VARIABLES
Textbook
Odessa – 2012
УДК 510(083) |
План НМВ 2011/2012 уч.г. |
Составители:
Доц. В. Н. Гавдзинский, ст. преп. Л. Н. Коробова, ст. преп. Е. В. Мальцева
Методическое пособие содержит основные определения, формулы и теоремы дифференциального исчисления функции многих переменных и предназначено для студентов академии, изучающих математику на английском языке.
Основные теоремы и формулы приведены с доказательством, а также даны решения типовых задач, задания для самостоятельной работы. Кроме того прилагаются комплексной контрольной работы.
2
|
CONTENTS |
|
1. |
Definitions .......................................................................................................... |
4 |
2. |
Ways of representation functions of two variables ............................................. |
5 |
3. |
Level curves ....................................................................................................... |
6 |
4. |
Limits and continuity............................................................................................ |
8 |
5. |
Partial increments and derivatives of the first order ........................................... |
10 |
6. |
Geometric interpretation of partial derivatives ................................................... |
12 |
7. |
Level surfaces. Quadric surfaces ......................................................................... |
13 |
8. |
Tangent plane and normal ................................................................................... |
15 |
9. |
Total increment and total differential of a function of two variables .................. |
16 |
10. |
Applying a total differential to approximate calculations.................................. |
17 |
11. |
Partial derivatives of the higher order .............................................................. |
18 |
12. |
Differentiating composite functions .................................................................. |
19 |
13. |
Directional derivative and gradient of a function of several variables ............. |
20 |
14. |
Extreme of a function of two variables ............................................................. |
22 |
15. |
The conditional extreme of a function of two variables .................................... |
25 |
16. |
The greatest and the least values of a function of two variables....................... |
28 |
17. |
Solution of problems ......................................................................................... |
30 |
18. |
Revision exercises ............................................................................................. |
38 |
3
1. Definitions
Until now we have studied functions of a single variable. Many phenomena in the physical world can be described by such functions, but most quantities actually depend on more than one variable. For example, the volume of a rectangular box depends on its length, width, and height; the temperature at a point of a metal plate depends on the coordinates of the point (and possibly on time as well). Any quantity that depends on several other quantities can be thought as determining a function of several variables.
A function of several variables consists of two parts: a domain (D(u)), which is a set of points in the plane or in space, and a rule, which assigns to each member of the domain one and only one real number. This rule can be written in the form u = f (P), where P D(u).
If D(u) is a part of the plane XOY then any point of this region has two coordinates: P = P(x, y) and we have a function of two independent variables. As a rule it is written in the form z = f (x, y).
If D(u) is a part of the space XYZ then any point of this region has three coordinates: P = P(x, y, z) and we have a function of three independent variables. Let us write it in the form u = f (x, y, z).
If D(u) is a part of an n-dimensional space then any point of this region has n coordinates: P = P(x1 , x2 ,..., xn ) and we have a function of n independent variables. Let us write it in the form u = f (x1 , x2 ,..., xn ).
Independent variables are equivalent and they are called the arguments.
To find a domain of a function of two variables we can use the same rules as for a function of one variable.
Example 1.1. Find the domain of the given function. z = f (x, y) if
|
|
|
|
|
|
|
|
b) f (x, y) = |
1 |
|
||
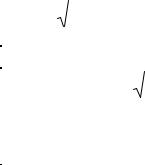
a) f (x, y) = y − x 2 |
||||||||||||
xy |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
Function |
|
Domain |
|||||||
|
|
|
|
|
|
|
|
|
D(z): y ≥ x 2 |
|||
|
a) |
|
z = y − x 2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
b) |
|
z = |
1 |
|
|
D(z): xy ≠ 0 |
|||||
|
|
xy |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Fig. 1.1 |
||||
4
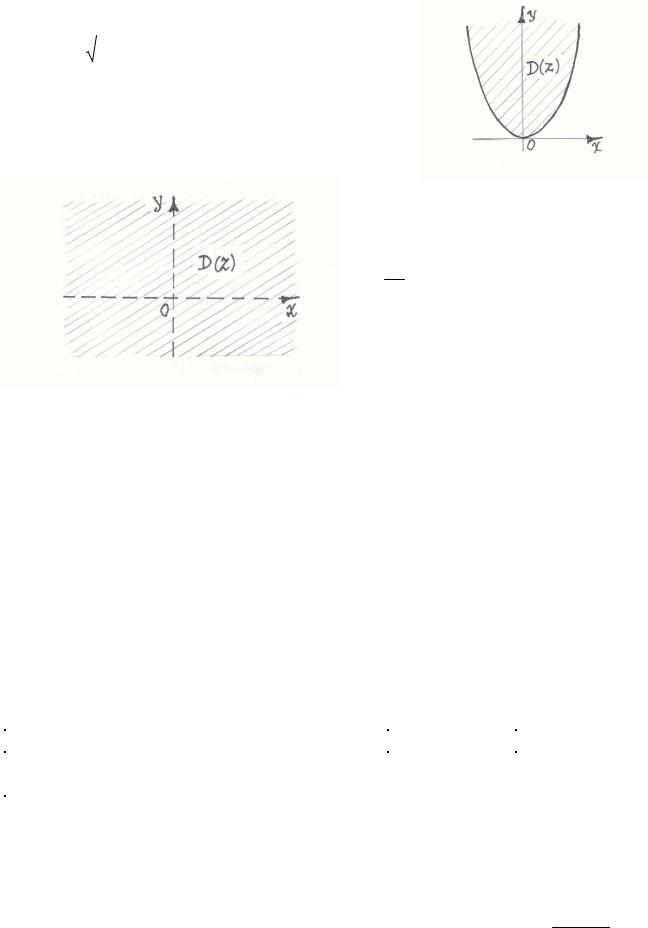
|
a) The domain of the function |
|
f (x, y) = |
|
|
y − x 2 are all points of xy-plane |
||
which are |
on the parabola y = x 2 and in |
|
the interior region of this parabola.
b) The domain of the function
z = 1 are all points of xy-plane except xy
the
points of x-axis and y-axis
2. Ways of Representation Functions of Two Variables
A function of two variables, like a function of one variable, can be specified by
atable, by a formula (analytically) or by its graph.
A.A tabular representation of a function indicates the values of the function for
anumber of pairs of values of the independent variables. For example, the table 2.1 shows dependence of area Sij on two independent variables
bi – a width and a j – a length.
|
a1 |
a2 |
… |
an |
b1 |
S11 |
S 12 |
… |
S 1n |
b2 |
S 21 |
S 22 |
… |
S 2n |
… |
… |
… |
… |
… |
bm |
S m1 |
S m2 |
… |
S mn |
Table 2.1
B. A function of two variables can be specified by formula. In the analytical specification of a function we use a formula determining the values of the function
xy
x2 + y2 .
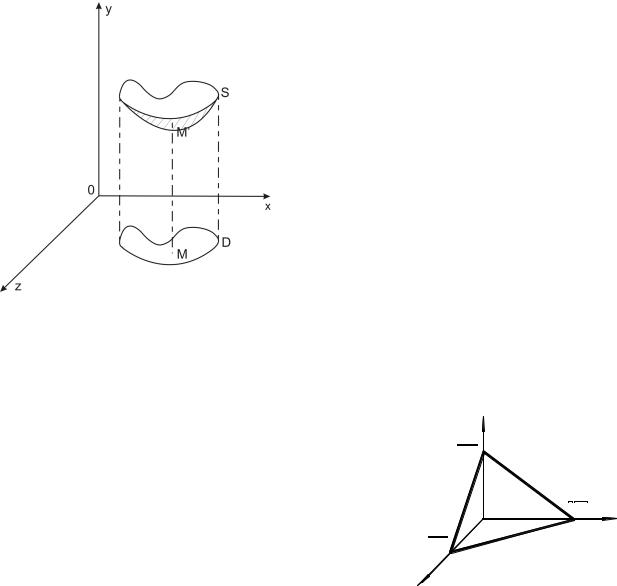
C. The function of two variables can be represented by its graph too.
The graph of a function z = f (x, y) is the collection of points (x, y, f (x, y)) and is represented by a surface S . Each point of this
surface |
M ′ has |
coordinates (x, y, z). |
The |
|
domain |
of |
the |
function z = f (x, y) is the |
|
region |
D |
of |
xy − plane. When |
point |
M (x, y) |
runs through region D , than |
point |
||
M ′(x, y, z) |
runs through the surface S , whose |
|||
equation is z = f (x, y). |
|
|||
Fig.2.1
|
|
Example |
2.1. |
|
The graph of a function |
|||
Ax + By + Cz + D = 0 |
is the plane passing through |
|||||||
|
|
|
|
|
D |
|
|
|
the points |
− |
|
, 0, 0 , |
|
||||
|
|
|||||||
|
|
|
|
|
A |
|
|
|
|
|
D |
|
|
|
|
D |
|
|
0, − |
|
, 0 |
, 0, 0, − |
|
. |
||
|
|
|||||||
|
|
B |
|
|
|
|
A |
|
In Fig.2.2 is drawn the portion of this plane in |
x |
|
the first octant. |
||
|
z
|
D |
|
|
C |
|
|
|
D |
|
O |
B |
|
|
|
D |
|
y |
A |
|
|
Fig.2.2
3. A Level Curves
Let f be a function of two independent variables x and y and denote the dependent variable by z. The equation z = f (x, y) may be interpreted as defining a surface S in xyz-space. If we cut the surface with planes z = h1 , z = h2 , we get contour lines on the surface. And if we project them onto the xy-plane, we obtain a level curves f (x, y) = h1 , f (x, y) = h2 in the domain of z = f (x, y) (Fig. 3.1).
6
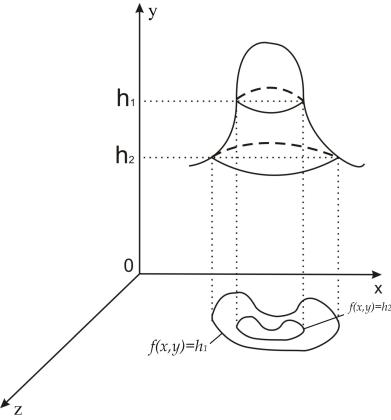
Fig. 3.1
Definition. The set of points in the xy-plane where function f (x, y) has a constant value C is called a level line of this function f (x, y) = C .
Level curves are particularly useful in engineering applications. For instance
equation z = (x − 2)2 circular plate, then distribution.
+ (y + 3)2 gave the celsius temperature at each point in a flat the level curves would be isotherms of the temperature
Example 3.1. Find the level lines of the function z = (x − 2)2 + (y + 3)2 .
Solution. The equation of the level lines of the given function is
(x − 2)2 + (y + 3)2 = C
If C takes different values, for example, C = 4, C = 9, C = 16,... we will have a family of circles with origin at a point O(2;−3) with corresponding radiuses R = 2, R = 3, R = 4,...
7

Example3.2. Let f (x, y) = 8 − 2x − 4 y . Sketch the graph of f, and determine the level curves.
Solution. If we let z = f (x, y), then the given equation becomes z = 8 − 2x − 4 y
This is an equation of a plane with x intercept 4, y intercept 2, and z intercept 8.
The portion of the plane in the first octant is sketched in Fig.3.2. For any value of C, the level curve
f (x, y) = C is the straight line
in the xy plane with equation 2x + 4 y − 8 + C.
The level curves are parallel lines.
Fig.3.2
4. Limits and Continuity
Definition. The limit of a function f (x, y) as (x, y) → (x0 , y0 ) is a number A if for any ε > 0 there exists a number δ > 0 such that for all points (x, y) ≠ (x0 , yo ) in
domain of f (x, y), from |
|
x − xo |
|
< δ |
and |
|
y − y0 |
|
< δ |
follows |
|
|
f (x, y) − A |
|
< ε . |
||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
Properties of Limits |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Let lim |
|
f (x, y) = A |
|
lim |
|
g(x, y) = B |
|
|
be given, then the |
|||||||||||
|
(x, y )→(x0 , y0 ) |
|
(x, y )→(x0 , y0 ) |
|
|
|
|
|
|
|
|
|
|
||||||||
|
following rules hold |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
lim |
[ f (x, y) + g(x, y)]= A + B |
|||||||||
|
Sum rule |
|
|
|
|
|
|
|
(x, y )→(x0 , y0 ) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
[ f (x, y) − g(x, y)]= A − B |
|||||||||
|
Difference rule |
|
|
|
(x, y )→(x0 , y0 ) |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
lim |
[ f (x, y) g(x, y)]= A B |
|||||||||
|
Product rule |
|
|
|
(x, y )→(x0 , y0 ) |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Constant multiple rule |
|
|
|
|
|
lim |
kg(x, y) = kB , k is constant |
|||||||||||||
|
|
|
|
|
|
|
|
|
(x, y )→(x0 , y0 ) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
lim |
|
f (x, y) |
= |
A |
if B ≠ 0 |
|||||
|
Quotient rule |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
(x, y )→(x0 , y0 ) g(x, y) |
|
|
|
B |
|||||||||||||
8

Example 4.1. Find limits of the functions:
a)lim (x2 + y2 ),
(x, y )→(3,4)
1 |
|
|
b) lim |
|
, |
|
||
(x, y )→(0,0) x + y |
|
|
c) |
lim |
|
|
|
|
|
x 2 + y 2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(x, y )→(0,0) |
|
|
x 2 |
+ y 2 + 1 − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
Solution: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a) |
lim |
(x 2 + y 2 )= 32 |
+ (− 4)2 |
= 9 + 16 = 25; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
(x, y )→(3,4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b) |
lim |
|
1 |
|
= |
|
1 |
|
= ∞ ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(x, y )→(0,0) x + y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 + y2 )( |
|
|
|
|
+ 1) |
|||||||||||||||||
|
|
|
|
|
|
|
|
x2 + y2 |
|
|
|
|
0 |
|
|
|
|
x |
2 + y2 + 1 |
|||||||||||||||||||||
c) |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||
( |
) |
( |
) |
|
|
x |
2 |
+ y |
2 |
|
+ 1 |
|
|
|
|
|
( ) |
( ) |
|
x |
+ y |
+ 1 |
− 1 |
|
|
|||||||||||||||
|
x, y → 0,0 |
|
|
|
|
|
− 1 0 |
|
|
x, y → 0,0 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
lim |
|
x2 + y2 + 1 + 1 = 2 . |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x, y )→(0,0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Definition. A function f (x, y) is said to be continuous at the point |
(x0 , y0 ) if: |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
1) |
|
f (x, y) is defined at (x0 , y0 ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2) |
|
|
lim |
|
f (x.y) exists, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
(x, y )→(x0 , y0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
3) |
|
|
lim |
|
|
|
|
f (x, y) = f (x0 y0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
(x, y )→(x0 , y ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
For a function |
|
f (x, y) fair all properties of the continuous functions similar to |
||||||||||||||||||||||||||||||||||||||
functions |
of |
one |
|
variable. For example, |
the |
function |
z = |
|
|
|
|
1 |
|
|
is |
continuous |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
+ y 2 |
|
|
||||||
everywhere, |
except the |
point (0,0). For |
the |
function |
z = |
|
|
|
|
1 |
|
|
|
the |
points of |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
x |
2 |
− y 2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
discontinuity are all points for which y = x or y = − x .
9
5. Partial Increments and Derivatives of the First Order
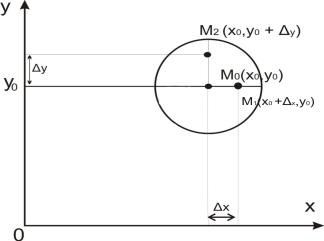
Definition. An open r-neighborhood of a given point M 0 (x0 , y0 ) is the set of all points lying inside the circle of radius r and center at the point M 0 .
Let a function z = f (x, y) be defined in a neighborhood of a point M 0 (x0 , y0 ) and
points M1 (x0 + |
x, y0 ), |
M 2 (x0 , y0 + |
y) belong to this |
neighborhood too.
Fig. 4.1
Definition. |
A difference f (x0 + |
x, y0 ) − f (x0 , y0 ) |
is called the partial |
|||||||||||||||
increment of the function z = f (x, y) with respect to x and is denoted by |
x z . |
|||||||||||||||||
Similarly, |
f (x0 , y0 + |
y) − f (x0 , y0 ) = |
y z. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x z |
|
|
|
|
|||
It should be noted, that a ratio |
|
|
|
can be considered as a function of one |
||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||
|
|
|
|
x and a ratio |
|
y z |
|
|
|
|
||||||||
variable with respect to |
|
|
|
|
- with respect to |
y . |
|
|||||||||||
|
y |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Definition.The limit of a ratio of partial increment of the function |
z = f (x, y) |
|||||||||||||||||
with respect to |
x to the increment |
|
|
x , |
as |
x tends to zero, is called a partial |
||||||||||||
derivative of function z = f (x, y) with respect to x |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
x→0 |
x |
|
|
||||
Partial derivative with respect to |
x |
of the function z = f (x, y) can be denoted |
||||||||||||||||
by one of the ways: |
∂z |
, |
z′ , |
f |
|
′ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
∂x |
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
By analogy, lim |
y z |
= |
|
∂z |
= z |
′ |
= f ′ . |
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||||
|
y→0 |
y |
|
|
∂y |
|
y |
|
y |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
The partial derivatives |
z′ |
|
and z ′ |
are functions of two variables. But when we |
||||||||||||||
|
|
|
|
|
x |
|
|
y |
|
|
|
|
|
|
|
|
||
were finding z′ we assumed that the variable |
y is constant. It means that for finding |
|||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
partial derivatives we can use formulas and theorems for function of the one variable.
10
