Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская национальная академия связи им. А.С. Попова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Functions of several variables- Textbook..pdf

.pdf

Скачиваний:

Добавлен:

10.02.2016

Размер:

1.51 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Solution. Find the coordinates of the vector M 0 M1 :

a = M 0 M 1 = (xM1 − xM 0 ; yM1 − yM 0 )= (6 − 3; 6 − 2) = (3; 4)

Find partial derivatives of the given function:

∂z = (5xy − x 2 y 2 )′ x = 5 y − 2xy 2 ;

∂x

∂z = (5xy − x 2 y 2 )′ y = 5x − 2x 2 y

∂y

Using the formulas (13.1) and (13.2) we have

∂z(M

0 )

= (5 y − 2xy 2 )

x=3

+ (5x − 2x 2 y)

x=3

∂a

9 + 16

y=2

= −14 0.6 + (− 21) 0,8 = −25.2.

The vector which coordinates are the values of partial derivatives of the first order at a point M 0 (x0 , y0 , z0 ) is called gradient vector of a function u = f (x, y, z)

at a point M 0 (x0 , y0 , z

0 )

z(M

) = (u

′

); u′

))

(13.3)

grad

Gradient vector points in the direction of the greatest rate of the change of the function and whose magnitude is the greatest rate of change

				∂u (M			) 2
grad z(M		)				0
			=
	0
					∂x

	∂u (M	0	) 2	∂u (M		0	)	2
+				+				(13.4)

	∂y				∂z

Example 13.2. Find the direction of the greatest rate of the change of the

function u = x2 y3 and

magnitude of

the

greatest

rate of the change at the point

M 0 (1;2).

Solution. In this case the formula (13.4) has the form

∂u (M

)

∂u

)

grad z(M

)

∂x

∂y

∂u (M 0 )

(x 2 y

3 )

= (2xy

3 )

′

= 16 ,

∂x

x 1

y=2

∂u (M 0 )

= (x 2 y 3 )y ′

= (3x 2 y 2 )

x=1 = 12,

∂y

x 1

y=2

Then

z(M 0 ) = (16;12)

grad

z(M

)

= 16 2 + 12 2

and

grad

400 = 20 .

14. Extreme of a Functions of Two Variables

Definition 14.1. A function z = f (x, y) has minimum (maximum) at a point

M 0 (x0 , y0 ) if f (x0 , y0 ) < f (x, y) ( f (x0 , y0 ) > f (x, y)) for all points which belong to sufficiently small neighborhood of a point M 0 (x0 , y0 ).

Definition 14.2. The points at which a function z = f (x, y) has maximum or minimum are called the points of extreme of the function.

Definition 14.3. The points at which partial derivatives of the first order do not exist or equal to zero are called the critical points or points suspicious on extreme.

Definition 14.4. The points at which all partial derivatives of the first order exist and are equal to zero are called the critical (stationary) points.

Example 14.1. Find critical points of the function

z = x 2 − xy + y 2 + 3x − 2 y + 1.

Solution: Find partial derivatives

z′

= 2x − y + 3;

z′

= − x + 2 y − 2 .

These derivatives exist for all x and

y . It means that function have stationary points

if z′

= 0 and z

′

= 0 .

Make up the system of the equations

z′

= 0

x = −

2x − y + 3 = 0

2x − y = −3

3 .

′

= 0

− x + 2 y − 2 = 0

− x + 2 y = 2

z y

y =

Hence the point M 0

−

;

is the stationary point of the given function.

3 3

Theorem 14.1. (the necessary conditions for extreme).

If a differentiable function z = f (x, y) attains an extremum at a point M 0 (x0 , y0 ) its partial derivatives turn into zero at that point:

						∂ z
						∂ z		= 0,

						∂ x
						∂ x		x=x0

								y= y0
								y= y0
z =	f (x, y) has extremum at	M	0	(x0	, y0 )
z =	f (x, y) has extremum at	M	0	(x0	, y0 )
						∂ z
							= 0.
							= 0.
						∂y		x=x0
								y= y0

In other words a point M 0 (x0 , y0 ) is a critical point of the given function.

Proof.

Let the function z = f (x, y) have an extremum at the point M 0 (x0 , y0 ). Let y be fixed: y = y0 . It means that the function z = f (x, y0 ) is the function of one variable.It follows from the condition of the theorem, that this function has extremum at the point x = x0 . Hence, its derivative with respect to x should be equal to zero at

∂ z

the point x = x0 . That is

= 0 . Similarly we get

= 0 . The theorem

∂ x

x=x0

∂ y

x=x0

is proved.

y= y0

As we know the equation of the tangent plane to the surface z = f (x, y) is

z − z

= f ′ (x

, y

) (x − x

) + f ′ (x

, y

) (y − y

It is clear that it turns to

z = z0 for a stationary point M 0 (x0 , y0 ).

Thus, geometric meaning of this theorem is:

If a differentiable function z = f (x, y)

attains an exstremum at a point

M 0 (x0 , y0 ), then the tangent plane to the surface at the corresponding point should be parallel to the coordinate plane of the independent variables.

• • Let the function z = f (x, y) be continuous together with its partial derivatives of the first and the second orders and let a point M 0 (x0 , y0 ) be a stationary point of this function. Denote

∂ 2 z(M			0	)		∂ 2 z(M	0	)		∂ 2 z(M	0	)
			0		= A;		0		= B;		0		= C , and form
∂	x	2			= A;	∂x∂y			= B;	∂ 2			= C , and form
	x									y

− 3 y.

			∂ 2 z(M		0	)	∂ 2 z(M	0	)
					0			0
(M		) =	∂x	2			∂x∂y				A B	= AC − B 2 .
				2
	0					)	∂ 2 z(M		)	=
	0		∂ 2 z(M		0	)	∂ 2 z(M	0	)		B C
			∂x∂y				∂y 2

Theorem 14.2. (the sufficient conditions for extreme).

If (M 0 )>0 the function z = f (x, y) has extreme at a point M 0 (x0 , y0 ) which is maximum if A < 0 and minimum if A > 0 .

If AC − B 2 < 0 there is no extreme of the given function at the point M 0 (x0 , y0 ). Note, that the point M 0 (x0 , y0 ) is called a saddle point.

If AC − B 2 = 0 the properties of the second derivatives do not provide any answer to the question of existence of an extreme and further investigation will be needed.

Example. Find the extrema of the function z = x 2 − 2xy + 1 y 3 3

Solution.

The given function is continuous and differentiable everywhere in the xy-plane.

∂ z

= 0,

∂ x

find the critical points of the given function.

1). Using the conditions

∂ z

= 0.

∂y

∂ z

′

= x

− 2xy +

− 3y

= 2x

− 2 y

= 0

x − y = 0

∂ x

∂ z

′

− 3 = 0

− 2x + y 2

= x

− 2xy +

− 3 y

= −2x + y

− 3

= 0

∂y

The solution of this system gives two stationary points M1 (3, 3) and M 2 (− 1, − 1). 2). To use the sufficient conditions for extreme evaluate the second derivatives

of the given function.

∂ z

′

(

)

′

− 2xy +

−

3 y

2x − 2 y

= 2,

∂ x 2

∂ 2 z

= (− 2x + y 2 − 3) ′

= 2 y,

∂y 2

∂ 2 z

(

)

′ = −2.

− 2 y

∂ x∂y

a) Consider the point M1 (3, 3).

∂ 2 z(M

)

∂

2 z(M

)

∂ 2 z(M

)

Hence

A =

= 2; B =

= −2;

C =

= 2 y

x=3 = 6 , then

∂x 2

∂x∂y

∂y 2

y=3

(M 1 ) =

− 2

= 12 − 4 = 8 > 0 , A = 2 > 0 and the function

− 2

has minimum at the point M1 (3, 3).

b) Consider the point M 2 (− 1, − 1).

∂ 2 z(M

2 )

∂ 2 z(M 2 )

∂ 2 z(M 2)

Hence

A =

= 2; B =

= −2;

C =

= 2 y

x=−1

= −2 , then

∂x 2

∂x∂y

∂y 2

y=−1

(M 2 ) =

− 2

= −4 − 4 = −8 < 0 , so the function has not

− 2

extremum at the point M 2 (− 1, − 1).

15. The Conditional Extreme of Functions of Two Variables

Definition. An extreme of function z = f (x, y) under condition ϕ (x, y) = 0 is called a conditional extreme of the function.

There are two methods of finding conditional extreme.

I.To find a conditional extreme by Lagrange method. To do it we need: 1). Write the Lagrange function

L(x, y, λ ) = f (x, y) + λϕ (x, y) , where λ is an arbitrary constant parameter.

2). Find critical points M k (xk , yk , λk ) of Lagrange’s function, using necessary condition of existence of the extreme

∂L

∂x∂L∂y

∂L

∂λ

=	0
=	0

=
=	0

=	0
=	0

	∂f	+ λ	∂ϕ	=	0
	∂x		∂x

	∂f	+ λ	∂ϕ	=	0
	∂y		∂y

ϕ (x, y)				=	0

3). Check sufficient conditions at every critical points of the function for existence of an extreme :

a) if at a point M k (xk , yk , λk ) the determinant of the third order

ϕ ′

) ϕ ′

)

) =

ϕ ′

) L′′

)

ϕ ′

) L′′

)

is positive, then a point M k is a point of maximum and

zmax = f (M k ) = f (xk , yk ):

b)if determinant (M k ) is negative, a point M k is a point of minimum

zmin = f (M k ) = f (xk , yk ).

II.To find a conditional extreme by the substitution method. To do it we need:

a)solve equation ϕ (x, y) = 0 for x ;

b)substitute this variable into the equation z = f (x, y);

c)examine the function of one variable for extreme.

Example. Let us determine the greatest value of the function z = x 2 y on condition that x and y are positive and satisfy the equation 4x + 5 y = 60 .

Solution.

I. Let us use the Lagrange method.

1)write the Lagrange function

L(x, y, λ ) = x 2 y + λ(4x + 5 y − 60);

2) find critical points

2x(60 − 4x)						2x(60 − 4x) + 20λ = 0
2x(60 − 4x)
		+ 4λ	= 0		5
		+ 4λ	= 0		5
5					4		2	,
	2	+ 5λ	= 0		4	4x	2	+ 20λ = 0
x		+ 5λ	= 0
			120x − 8x 2 − 4x 2 = 0
			120x − 12x 2 = 0
			10x − x 2	= 0

x(10 − x) = 0 x = 0, x = 10

x = 0 does not make sense,
y =	60 − 40	= 4	λ =	− 2xy	= −	xy	= −	10 4	= −20

5			4		2		2

So, critical point is M 0 (10;4;−20).

3) find (M 0 )

∂ 2 L	= 2 y,	∂ 2 L	= 0,	∂ 2 L	= 2x
∂x 2		∂y 2		∂x∂y

∂ 2 L(M	o	)		∂ 2 L(M	0	)		∂ 2 L(M	0	)
			= 8,				= 0,				= 20
∂x 2				∂y 2				∂x∂y

			∂ϕ	= 4,		∂ϕ	= 5
				= 4,			= 5
			∂x			∂y
		4	5
	0	4	5
(M 0 ) =	4	8	20		= 400 + 400 − 200 = 600 > 0
	5	20	0

4) x = 10 and y = 4 maximized the utility function which have maximum value

zmax = 10 2 4 = 400.

II.Let us use the substitution method.

1)Solve equation 4x + 5 y = 60 for x

y = (60 − 4x) , 5

2) Substitute y = (60 −	4x) in z = x 2 y
5
	z =	x 2	(60 − 4x)
				,
			5	,
			5

examine z =

x 2 (60 − 4x)

for extreme

Domain of the function z : D(z) = R

z′ =

2x(60 − 4x) + x 2 (− 4)

120x − 8x 2

− 4x 2

120x − 12x 2

z′ = 0 12x(10 − x) =

x = 0,

0 1

x2 = 10.

(

)

y = 12,

y = 60 − 4x

x2 = 4,

then we have two critical points M1 (0;12) and M 2 (10;4).

z′′ =	120 − 24	x=10 = −24 < 0 ,then


5

zmax = 10 2 4 = 400.

16.The Greatest and the Least Values of a Function of Two Variables

To find the greatest f max D (x, y)	and the least f min D (x, y) values of the
function z = f (x, y) in the closed region D	we need to find the extreme values of the

function at the points that lie inside of D , and on the boundary of the region. From these values choose the greatest and the least values. This numbers will be the greatest and the least values of the function z = f (x, y) in the closed region D .

x [0,6].

′z x

z′y

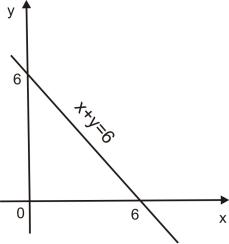
Example.

z= x 2 y(4 − x − x = 0,

Find	the greatest and the least values of the function
y) in the triangle bounded by the lines
y = 0,	x + y = 6 .

Fig. 16.1.

Solution.

Find the critical points inside the region

= 2xy(4 − x − y) − x 2 y = xy(8 − 3x − 2 y) = x 2 (4 − x − y) − x 2 y = x 2 (4 − x − 2 y) .

According to the necessary condition for the existence of the extreme of the function of two variables have a system of equations

xy(8 − 3x − 2 y) = 0
x 2 (4 − x − 2 y) = 0
Inside of the region x ≠ 0 and y ≠ 0 , then
3x + 2 y = 8	x = 2
x + 2 y = 4	y = 1 .

At the critical point M1 (2,1) we have z(2,1) = 4 .

Now we examine the function on the boundary of the triangle. On the straight line x + y = 6 variable y = 6 − x and function z takes the form

z = x 2 (6 − x) (4 − x + x − 6) = 2x 2 (x − 6),

zmin D

Let us find the least and the greatest volumes of this function of one variable

on the closed interval [0,6].
z′ = 6x 2 − 24x;	z′ = 0, 6x(x − 4) = 0 x = 0,	x	2	= 4
	1		2
Find the values of the function at the points x = 0,		x = 4, x = 6 .
	z(4) = −64, z(0) = 0, z(6) = 0 .
On the straight line y = 0 we have z = 0 .
On the straight line x = 0 we have z = 0 .
At the point (6,0)	z = 0 .
At the point (0,6) z=o.

So, the given function z have the greatest value at the point M1 (2,1) inside the region and the least value at the point M 2 (4,2) on the boundary of the region.

zmax D = 4 .

= −64

17. Solution of Problems

Problem 1. Let the function z =	y 2
		be given. Find:

52 x a) the total differential of the first order;

b) all partial derivatives of the second order.

Silution.

• a)

The total differential of the first order can be calculated using the formula

dz =

∂ z

dx +

∂ z

dy .

∂ x

∂ y

Calculate the partial derivatives of the first order:

∂ z

y 2 ′

y 2

′

y 2

= −

;

∂ x

52 x

52x

y =const

∂ z

y 2

′

(y 2 )′ =

∂ y

52x

26x

52x

x=const

So,

y 2

dz = −

dx +

dy .

52 2 x

26x

• b) Calculate

∂	2	z
∂		z	=	−
		2	=	−
∂ x		2
∂ x

the partial derivatives of the second order:

y	2		′		y	2	(x −2 )′		y	2	( − 2x −3 )′ =
				= −				= −

		2		52				52
52x
				x

y 2

26x 2

;

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.02.20163.53 Mб11Ekonom_inform_konspekt_zaoch.pdf
#
12.11.201969.63 Кб0electric current_прктик_раб.doc
#
10.02.20165.42 Mб9ELMAGN_lab_2_1-4_3_1-2.doc
#
10.02.20161.1 Mб27Filosofia.docx
#
10.02.201621.48 Кб13finansovaya_strategia_predpriatia_dlya_302.docx
#
10.02.20161.51 Mб19Functions of several variables- Textbook..pdf.pdf
#
10.02.20167.06 Mб22ga2ap.doc
#
10.02.201643.9 Mб39his_uk1.pdf
#
18.08.201940.66 Кб3INDIVIDUAL_NE_ZAVDANNYa_DO_TEMI_1.docx
#
10.02.2016684.03 Кб18ISDN Основные виды обслуживания.doc
#
31.08.201925.13 Mб2ISDN Основные виды обслуживания.doc