Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская национальная академия связи им. А.С. Попова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Functions of several variables- Textbook..pdf

.pdf

Скачиваний:

Добавлен:

10.02.2016

Размер:

1.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

∂

′

(y 2 )′ =

2 y

= −

−

= −

;

∂ x∂y

52x

26x

52x

∂ 2 z

′

′ =

;

∂ y 2

26x

′

1 ′

∂ 2 z

= −

∂ y∂ x

26x

26 x 2

Note that:

∂ 2 z

∂ y∂ x

∂ x∂y

Problem 2. Let the function u = e52 xz + 2 y , the point A(− 1;1;−1), and the vector

= (2; 2

52;52) be given. Find:

a) a gradient of the given function at the given point: (

grad f (A));

∂f (A)

b) a derivative of the function into direction of the vector

a at the point A:

∂a

Solution.

• a) Gradient of the given function at a given point we’ll find using the

formula:

∂ u

(

)

∂ u

(

)

∂ u

(

)

grad u(A) =

;

∂ x

∂y

∂ x

1)	∂u	= (e52 xz + 2 y )′	=	e52 xz + 2 y

	∂x		x

∂ u(A) = ∂ u(1;−1;1) = e52 xz + 2 y


	∂x		∂x
2)	∂u	= (e52 xz + y 2 )′		=	e52 xz + 2 y
2)		= (e52 xz + y 2 )′		=	e52 xz + 2 y
	∂y		y

52z

52z x=−1 = − 52e54 ;

y =1

z=−1

2 y

∂ u(A)

∂ u(1;−1;1)

= 2e

52 xz + 2 y

= 2e54 ;

x= −1

∂y

y =1

z =−1

∂u

= (e52 xz+ y2 )′

e52 xz + 2 y 52z

∂z

∂ u(A)

∂ u(1;−1;1)

= e52 xz + 2 y 52z

= − 52e54 .

x= −1

∂ z

y =1

z = −1

grad u(A) = (− 52e54 ;2e54 ;−52e54 ) grad u(A) = 2e54 (− 26;1;−26).

• b) Using the formula for finding a derivative of the function into direction of the

vector a at the point A we have:

∂ u(A)

∂a

∂x

∂ y

∂ z

a x2 + a y2

+ a z2

a x

= 2

= (2 + 52)2 =

= 2 52

a x2 + a y2 + a z2 = 2 2 + 4 52 + 522

a y

= 52

a z

∂u(A)

= −52e

= 2e

= −52e

∂x

∂y

∂z

(− 52e54 2 + 2e54 2

− 52e54 52)=

2e54

(− 26 +

− 52 13)=

2e54

(

− 702).

∂u(A)

2e54

(

− 702).

The answer:

grad u(A) = 2e54 (− 26;1;−26);

∂a

Problem 3. Investigate the function z = x 3 + y 3 − 3xy for extremum.

Solution.

∂z

= 0,

1. Find the critical points using the conditions

∂x

∂z

= 0.

∂y

∂z

∂(x 3

+ y 3

− 3xy)

2 − 3y

= 3x

∂x

. So we have the system:

∂z

∂(x 3

+ y 3

− 3xy)

= 3 y

− 3x

∂y

− 3 y = 0

− y

= 0

( )

(

)

− 3x = 0

− x

= 0

3 y

1). (1) y = x 2

(3)

2). (3) → (2) x 4

x = 0,

− x = 0 x(x 3 − 1)= 0 1

(4)

x2 = 1,

= 0

3). (4) → (3) 1

y2 = 1

Thus there are

two critical points: P1 (0;0) and P2 ( 1;1 ).

2. To answer the question if the point

P0 (x0 , y0 ) is the point of extremum or

not we must consider

= AC − B 2 where

∂ 2 z(P )

A =

B =

and C =

∂x

∂x∂y

∂y 2

1)if > 0 then extremum exists, and for A > 0 it is minimum,for A < 0 it is maximum,

2)if < 0 extremum doesn’t exist,

3)= 0 we can say nothing.

The second derivatives are

∂ 2 z

= (3x 2 − 3 y)′ x

= 6x,

∂x 2

y=const

∂ 2 z

= (3x 2 − 3y)′ y

= −3,

∂x∂y

x=const

∂ 2 z

= 6 y.

∂y 2

Consider the point P1 (0;0):

A =

∂ 2 z(0,0)

= 6x

= 0 ,

C =

∂ 2 z(0,0)

= 6 y

x=0 = 0,

∂x 2

x=0

∂y 2

y=0

B =

∂ 2 z(0,0)

= −3

x=0 = −3.

∂x∂y

y=0

− 3

= −9 < 0 extremum doesn’t exist at the point P (0;0).

− 3

b) Consider the point P (1,1 ): A =

∂ 2 z(1,1)

= 6x

= 6,

∂x 2

y=1

C =

∂ 2 z(1,1)

= 6 y

= 6,

B =

∂

2 z(1,1)

= −3

x=1 = −3 .

∂y

x=1

∂x∂y

y 1

− 3

= 27 > 0 extremum exists. As A = 6 > 0 it is

Thus we have

− 3

minimum.

min

(1,1 ) = (x 3 + y 3

− 3xy)

x=1

= 1 + 1 − 3 = −1.

y=1

The answer: z min (P2 ) = − 1 .

Problem 4. Find the domain of the function:

a) u =

b) u = lg(x 2 − y 2 + 2x + 4 y)

2 + 2 y 2 − 4

Solution.

• a)

u =

D(u): x 2 + 2 y 2 − 4 ≠ 0 .

x 2 + 2 y

2 − 4

First find the boundary whose equation is x 2 + 2 y 2 − 4 = 0.

x 2 + 2 y 2 − 4 = 0 x 2 + 2 y 2 = 4

x 2

y 2

= 1

x 2

y 2

= 1

(

2 2

The boundary of

the domain is the ellipse with

the center in the original and semi axes a = 2,

b = 2 . Hence the domain of the given function is the xy-plane except the points of the ellipse.

• b) u = lg(x 2 − y 2 + 2x + 4 y) D(u): x 2 − y 2 + 2x + 4 y > 0 .
The boundary of the domain of the given function is the curve
x 2 − y 2	+ 2x + 4 y = 0 . Completing the squares gives us
x 2 − y 2	+ 2x + 4 y = 0 (x + 1)2 − (y − 2)2 = −3	(y − 2)2			(x + 1)2
				−		= 1
		(		)2	(		)2
			3			3

The boundary of the domain is the hyperbola with the center at the point A(− 1, 2). Hence the domain of the given function is the outer part of the plane 0xy with respect to hyperbola. The hyperbola does not belong to the domain.

Problem 5. The function					y	e y / x	is given. Does this function satisfy the
Problem 5. The function					x2	e y / x	is given. Does this function satisfy the
					x2
equation	∂ z	+ y	∂ 2 z	= 0 ?
equation	∂ x	+ y	∂ y 2	= 0 ?
	∂ x		∂ y 2

Solution.

∂ z

= (e y / x )

′ = −

e y / x ;

∂ x

x 2

∂ z

= (e y / x )

′ =

∂ 2 z

′

e y / x

e y / x ;

∂ y

∂ y2

∂ z

∂ 2

/ x

e y /

+ y

= −

e y

+ y

x = 0

0 = 0 .

∂ x

∂ y

x 2

Thus the function

e y / x

satisfies the equation

∂ z

+ y

∂ 2 z

= 0 .

∂ y 2

∂ x

Problem 6. Using the total differential of the function of two variables calculate approximately 33.012 − 20.02 , knowing that ln2 ≈ 0.69.

Solution.

Let us consider the function z = f (x, y) = 3 x 2 − 2 y .

Assume

x0 = 3, x1 = 3.01 x = 0.01,
y0 = 0, y1 = 0.02 y = 0.02	,

= f (3; 0.02) = 3

32 − 20

= 2 ,

then the desired value is

z = f (3; 0.02) = 3 3.012 − 20.02 .

Using the formula (10.1) we have

z1 ≈ z0 + d z ,

where dz =

∂ z

x +

∂ z

y .

∂ x

x=x0

∂ y

x=x0

y= y0

∂z

∂x

∂z

∂y

= (3

) ′

2 − 2 y

x=3

≈ 0.33 3,

x=x0

3 4

y=0

y= y0

(x − 2

)

x=3

= (3

) ′

− 2 y ln 2

y=0

− 0.69

≈

= − 0.058,

2 − 2 y

x=3

x=x0

3 2

3 4

y=0

y= y0

(x − 2

)

x=3

y=0

then

3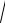3.012 − 20.02 = [z1 ≈ z0 + d z]= 2 + 0.333 0.01 − 0.058 0.02 = 2.004 .

Answer: 33.012 − 20.02 ≈= 2.004.

Problem 7. Find equations of the tangent plane and normal of the surface z = x 2 + xy + y 2 at the point M (1, 2, 7).

Solution.

1) To find the equation of the tangent plane use the equation (8.5)

z − z

= f

′ (x

, y

) (x − x

) + f ′ (x

, y

) (y − y

where x0 = 1, y0 = 2, z0 = 7;

f ′

, y

)

= (x 2

+ xy + y 2 ) ′

= (2x + y)

x=1 = 4,

x 1

y=2

f ′

, y

)

= (x 2

+ xy + y

2 ) ′

y=2

= (x + 2 y)

x=1 = 5.

x 1

y=2

So the equation of the tangent plane is

z= 7 + 4(x − 4) + 5(y − 5) z = 4x + 5 y − 34.

2)To find the equations of the normal line use the equation (8.4)

z − z0	=	x − x0					=			y − y0									z − 7		=	x − 1	=	y − 2
																									.
		f ′ (x	0	, y	0	)			f	′ (x		0	, y		0	)			1			4		5	.
		f ′ (x		, y		)			f	′ (x			, y			)			1			4		5
		x							y
Answer: z = 4x + 5 y − 34,								z − 7			=			x − 1			=	y − 2		.
Answer: z = 4x + 5 y − 34,											=						=			.
							1						4						5

				18. REVISION EXERSISES
	The values of the parameters a, b, c in the conditions of variants are:
a – the first letter of your surname
b – the first letter of your name
c – the first letter of your patronymic

1	2	3	4		5	6	7	8	9

А	В	С	D		Е	F	G	H	I

J	K	L	M		N	O	Р	Q	R

S	T	U	V		W	X	Y	Z

Variant 1.

1.Let the function z = (b + 1) y be given. Find:

a)differential of the first order);

b)partial derivatives of the second order.

2. Let the function u = x 2 + (c + 2)xy 3 + z 2 , the point A(1;2;−1) and the vector a = (2; 2a + 1; a + 1) be given. Find:

a) the gradient of the given function at a given point ( grad f (A))

∂f (A) b) derivative of the function into direction of the vector a at the point A .

∂a

3. Investigate the function z = x 3 + 3xy 2 − 15x − 12 y for extremum.

4. Find the domain of the function :

a) z = 9 y 2

− x 2 y 2 ;

b) z =

x2 + y2

5. The function

z =

is given. Does this function satisfy the equation

(x 2 − y 2 )5

∂ z

−

= 0 ?

x ∂ x y ∂ y

y 2

6. Using the total differential of the function of two variables calculate approximately (1.02)4.05

7. Find equations of the tangent plane and normal of the surface	z =	x	2	+	y	2	at the

		4			9
point M (2, 3, 2).		4			9
point M (2, 3, 2).

Variant 2.

1. Let the function z = ln (b + 2) y be given. Find:

a)differential of the first order

b)partial derivatives of the second order.

2. Let the function u = (c + 1) x ln y + z 3 , A(1;1; 2)the point A(1;2;−1) and the vector

= (2; 2

c + 1; c + 1) be given. Find:

the gradient of the given function at a given point (

grad f (A)),

∂f (A)

derivative of the function into direction of the vector

a at the point A

∂a

3. Investigate the function z = x 3 + y 3 − 9xy for extremum.

4. Find the domain of the function:

a) z = arcsin

;

x 2

z =

1 + x 2 + y 2

The function z = x y

is given. Does this function satisfy the equation

∂ 2 z

− (1 + ylnx)

∂ z

= 0 ?

∂ x∂ y

∂ x

Using the total differential of the function of two variables calculate approximately

8.042 + 6.032 .

Find equations of the tangent plane and normal of the surface z = 9 − x 2 − y 2

at the point M (1, 2, 2).

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.02.20163.53 Mб11Ekonom_inform_konspekt_zaoch.pdf
#
12.11.201969.63 Кб0electric current_прктик_раб.doc
#
10.02.20165.42 Mб9ELMAGN_lab_2_1-4_3_1-2.doc
#
10.02.20161.1 Mб27Filosofia.docx
#
10.02.201621.48 Кб13finansovaya_strategia_predpriatia_dlya_302.docx
#
10.02.20161.51 Mб19Functions of several variables- Textbook..pdf.pdf
#
10.02.20167.06 Mб22ga2ap.doc
#
10.02.201643.9 Mб39his_uk1.pdf
#
18.08.201940.66 Кб3INDIVIDUAL_NE_ZAVDANNYa_DO_TEMI_1.docx
#
10.02.2016684.03 Кб18ISDN Основные виды обслуживания.doc
#
31.08.201925.13 Mб2ISDN Основные виды обслуживания.doc