Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская национальная академия связи им. А.С. Попова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Functions of several variables- Textbook..pdf

.pdf

Скачиваний:

Добавлен:

10.02.2016

Размер:

1.51 Mб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Example 5.1. Find partial derivatives of the functions:

a) z = x3 + y 5 − 6 ,				b) z = x 2 y 3 ,
c) z = ln(x 2 y − y3 x5 + 7).
Solution:
a)	For finding z′	we		regard y as a constant and differentiate with respect
	x
to x :
z′	= (x3 + y 5 − 6)′ x			= 3x 2 ;
z′	= (x3 + y 5 − 6)′ x			= 3x 2 ;
x
			y=const
	= (x3 + y 5 − 6)′ y		y=const
z′				= 5x 4 .
z′				= 5x 4 .
y
			x=const
			x=const

b) z = x 2 y 3 .

z′	= (x 2 y 3 )′ x	= y 3 (x 2 )′ x = y 3 2x = 2xy 3 ;
x
		y=conwt
		y=conwt
z′	= (x 2 y 3 )′ y	= x 2 (y 3 )′ y = x 2 3y 2 = 3x 2 y 2 .
y

x=const

c)z = ln(x2 y − y3 x5 + 7).

				2xy − 5 y 3 x 4
z′	= (ln(x 2 y − y 3 x5 + 7))′ x		=	2xy − 5 y 3 x 4	;
z′	= (ln(x 2 y − y 3 x5 + 7))′ x		=		;
x				x 2 y − y 3 x5 + 7
		y=const
		y=const
z′	= (ln(x 2 y − y 3 x5 + 7))′ y		=	x 2 + 3y 2 x5	.
				x 2 + 3y 2 x5

y				x 2 y − y 3 x5 + 7
		x=const
		x=const

6. Geometric Interpretation of Partial Derivatives

		The plane y = y0 cuts the surface		z = f (x, y) in the curve z = f (x, y0 ). At
each x, the slope of this curve is f ′ (x, y			0	).
		x	0
		Similarly, the plane x = x0 cuts the surface in a curve whose slope is
f ′ (x	0	, y).
y	0

Fig. 6.1

The geometric interpretation of													partial derivatives of the function
z = f (x, y) is the that:
f ′ (x	0	, y	0	) is equal to the slope at the point P (x													0	, y	0	, z	0	) of the curve
x	0		0													0	0		0		0
z = f (x, y0 ) in which the plane y = y0 cuts the surface																	z = f (x, y).
Thus, in Fig.6.1, if x, y and z are measured in the same units
		tan α =			∂ z				= f ′	(x			, y			).
					∂ z
											0			0
					∂ x				x		0			0
						(x	, y		)
						(x	, y		)
				0			0
Similarly,
		tan β =			∂ z				= f ′ (x				, y			).
					∂ z
												0			0
					∂ y				y			0			0
					∂ y	(x	, y	0	)
				0				0

7. Level Surfaces. Quadric Surfaces

Definition. Let a function of three variables f (x, y, z) be given. For any number C the set of points (x, y, z) for which f (x, y, z) = C is called a level surface of f, and we identify a level surface with the corresponding equation f (x, y, z) = C .

Level surfaces of functions of three are analogous to level curves of functions of two variables.

We observe that the graph of any function f of two variables is a level surface. We need only let

g (x, y, z) = z − f (x, y)

and notice that g (x, y, z) = 0 if and only if z = f (x, y)

Thus the level surface g (x, y, z) = 0 is the graph of f , or equivalently, the graph of the equation z = f (x, y). This is why we call the graph of a function of two variables a

surface.

In sketching a level surface we will use the intersections of level surface with planes of the form x = c or y = c , as well as those of the form z = c . In each case the intersection of the level surface with the plane is called the trace of the level surface.

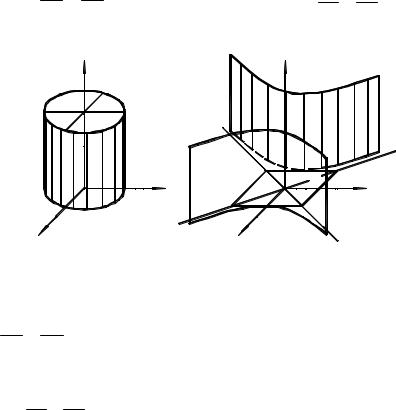
a) Elliptic Cylinder

х2	+ у2	= 1
а2	b2
	z
		b
	a
		y
x

b) Hyperbolic Cylinder
х2	− у2	= 1
а2	b2
z
b	y
b
a
x

a) The trace of the elliptic cylinder in any plane parallel to the xy plane is the

х2 у2

ellipse а2 + b2 = 1 . If a = b , the surface is a circular cylinder.

b) The trace of the hyperbolic cylinder in any plane parallel to the xy plane is the

х2 у2 hyperbola а2 − b2 = 1 .

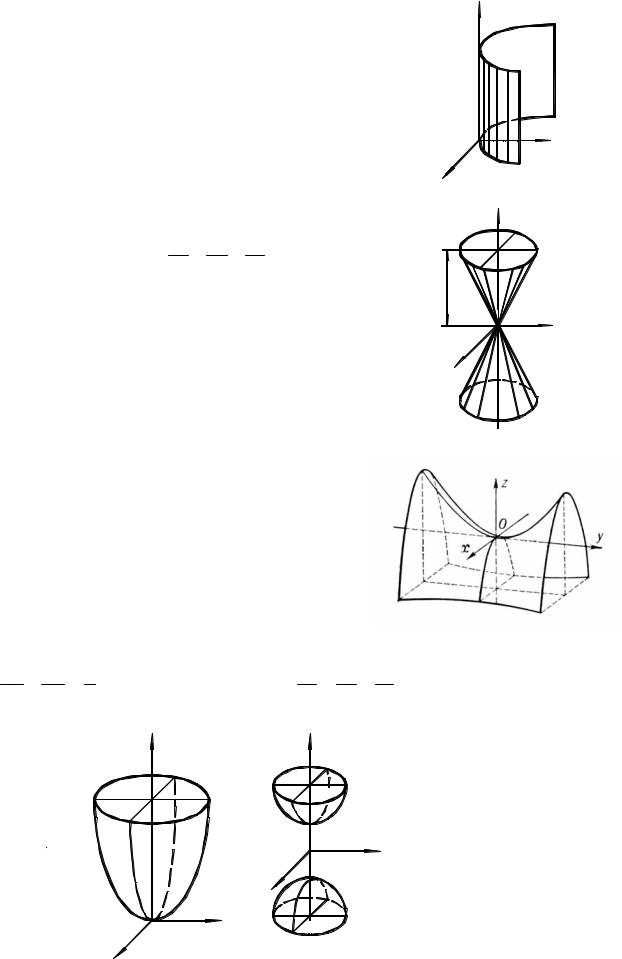
Parabolic Cylinder x 2 = 2 py

The trace of the parabolic cylinder in any plane parallel to the xy plane is the parabola x 2 = 2 py .

						y
						x
						z
х2	+	у2	−	z2	= 0	b
d) Elliptic Double Cone а2	+	b2	−	c2	= 0	a
d) Elliptic Double Cone а2		b2		c2
The trace of the cone in any plane parallel to the xy plane						c
The trace of the cone in any plane parallel to the xy plane
is either an ellipse (a circle if a = b ) or a point. The traces						y
in the yz and xz planes consist of two straight lines through
the origin.						x
If a = b , the surface is called a circular double cone.

ó2			−	õ2		=	z
e) Hyperbolic Paraboloid
	b	2		à	2		c

The traces in the yz and xz planes are parabolas. The trace in the xy plane consists of two intersecting lines. The trace in any other plane parallel to the xy plane is a hyperbola. The surface has the appearance of a saddle.

f) Elliptic Paraboloid

g) Two-sheeted Hyperboloid

õ2 + ó2 = z

à2 b 2 c

х2	+	у2	−	z2
а2	+	b2	−	= −1
а2		b2		c2
	z
a	b
			y
x
14

The trace of the paraboloid in any plane parallel to the xy plane is either an ellipse (a circle if a = b ), or empty. The traces in the yz and xz planes are parabolas. If a = b , the surface is called a circular paraboloid.

g) Problem 1. Denote the traces of the two-sheeted hyperboloid.

h) One-sheeted Hyperboloid i) Ellipsoid

х2	+	у2	−	z 2	х2	+	у2	+	z2
а2	+		−	= 1	а2	+		+	= 1
а2		b2		c2	а2		b2		c2
					z
					b			z
				a	b
				a
		c						c
					y			c		y
					y				b

				x			a
				x			a
					x

Problem 7.1. Denote the traces of the one-sheeted hyperboloid and the ellipsoid.

8.Tangent Plane and Normal Line

Let z = f (x, y) be a differentiable function at a point (x0 , y0 ,). Consider the sections of the surface S representing this function by the planes x = x0 and y = y0 . Let

M 0Tx	and M 0Ty be the tangent	lines at the
point	M 0 (x0 , y0 , z0 ) (see Fig.8.1)	to the plane

curves obtained in the sections. The plane T passing through these lines which meet at the point M 0 is called the tangent plane to the surface S at the point M 0 . The point M 0 is called the point of tangency (the point of contact) of the plane T and the surface S.

Fig.8.1

The straight line through M 0 normal to the tangent plane is called the normal line to the surface S at the point M 0 .

Let us find equations of the tangent plane and the normal line.
The straight line M 0Tx															is in the plane								y = y0 parallel to the plane Oxz. Its slope
relative to the x-axes is equal to f ′ . Therefore the equations of the line M T																																			are
															x																			0 x
		z − z					0	= f ′ (x				0	, y	0	) (x − x			0		),		y = y			0										(8.1)
							0		x			0		0				0							0
The equations of the straight line M 0Ty are found similarly:
		z − z					0	= f ′ (x				0	, y	0	) (y − y				0		),	x = x			0									(8.2)
							0		y			0		0					0						0
An equation of the plane T through M 0 (x0 , y0 , z0 ) can be written as
		z − z0 = A(x − x0 ) + B(y − y0 )																																	(8.3)
The straight lines M 0Tx											and M 0Ty are in the plane T, so the coordinates of the points
of these lines					satisfy the								equation of									the	plane. Substituting the											expressions of
z − z0 and	y − y0 from (8.1) into the equation (8.3) we obtain
f ′(x	0	, y	0		) (x − x					0	) = A(x − x					0	) A = f ′							(x		0	, y			0	)
x	0		0							0						0							x			0				0
Furthermore, we similarly find that
B = f		′ (x		0		, y		0	)
		y		0				0
Thus, the equation of the tangent plane takes the form
		z − z					0	= f ′ (x				0	, y	0	) (x − x			0		) + f ′ (x				0	, y			0	) (y − y			0	)		(8.4)
							0		x			0		0				0				y		0				0				0

It is clear that equations of the normal line are

z − z0	=	x − x0					=
		f ′(x	0	, y	0	)

		x

y − y0					(8.5)
f ′ (x	0	, y	0	)

y

9. Total increment and Total Differential of a Function of Two Variables

			Let a function							z = f (x, y)					be continuous on some set								D and have			z	′	, z′		in
																											x		y
this set. Let us take arbitrary point M 0 (x0 , y0 ) D , then
								z(M			0	) = z′	(x	0	, y	0	) x + z′ (x	0	y	0	)	y + αx + βy ,		(9.1)
											0	x		0		0	y	0		0
will be the total increment at this point, where α , β are infinitesimal values as
	x → 0 and						y → 0 .
							Definition. A function f (x, y) is differentiable at (x0 , y0 ) if
f	x	′ (x	0	, y	0	), f	′ (x	0	, y	0	) exist and the equation (9.1)											holds for	f (x, y) at (x		0	, y		0	).
	x		0		0		y	0		0															0			0

We call f (x, y) differentiable if it is differentiable in its domain.

Definition. The principal linear part with respect to increment z is called total differential of the function z

dz(M	0	) = z′	(x	0	, y	0	) x + z′	(x	0	y	0	) y .
	0	x		0		0	y		0		0

x and y , of a total

(9.2)

Example. The factory manufactures right circular cylindrical storage tanks that are 25m high with radius of 5m. How is sensitive tank’s volume to small variations in height and radius?

Solution. A tank’s volume is

V = π r 2 h .

So V is a function of two variables r and h. Then the change in volume caused by

small changes dr and dh

in radius and height is approximately

dV = V ′(5;25)dr + V ′ (5;25)dh = (2π r h)

(5;25)

dr + (π r 2 )

dh =

(5;25)

= 250π dr + 25π dh

The volume of cylinder is more sensitive to the small change in r

than it is to

an equally small change in h .

In contrast, if the values of r and h are reserved to make r = 25

and h = 5 ,

then full differential in V becomes

dr + (πr

2 )

dV = V ′(25,5)dr + V ′ (25,5)dh = (2πrh)

(25,5)

dh = 250πdr + 625πdh

Now the volume is more sensitive to changes in h than to changes in r .

From this example we can make the conclusion:

Functions are most sensitive to small changes in the variables that generate the largest partial derivatives.

10. Applying a Total Differential to Approximate Calculations

A total differential and a total increment of a function z = f (x, y) at a point

M 0 (x0 , y0 ) are:
dz(M	0	) = z′	(x	0	, y	0	) x + z′	(x	0	y	0	) y
	0	x		0		0	y		0		0

z(M 0 ) = f (x0 + x, y0 + y) − f (x0 , y0 ).

Because dz(M 0 ) = z(M 0 ) when x → 0 and y → 0 , than

f (x	0	+	x, y	0	+	y) ≈ f (x	0	, y	0	) + z′	(x	0	, y	0	) x + z′	(x	0	y	0	) y . (10.1)
	0			0			0		0	x		0		0	y		0		0

The formula (10.1) allows us to find approximate value of the function of two variables.

Example. Find approximate value of the function z = x 2 + 2xy + y at the point

M (1.03;1.97).
				Solution.
Let M 0 (1,2), than x = 0,03 and					y = −0,03. Find partial derivatives and
calculate their values at the point M 0 (1,2).
		∂z		= 2x + 2 y		∂z(M 0 )		= 2	1 + 2 2	= 6 ,
		∂x				∂x

	∂z		= 2x + 3y 2		∂z(M 0 )		= 2 1 + 3 22 = 14 ,

	∂y					∂y

Using the formula (10.1), we obtain

z(M ) ≈ 13 + 6 0,003 + 14 (− 0,03) = 13 + 0,18 − 0,42 = 12,76 .

11. Partial Derivatives of the Higher Order

Partial derivatives of the first order z′	and z ′	of a function z = z(x, y), in
x	y

general, are functions of two variables. From them we can find derivatives of the second order with respect to x and y

z′′	, z′′	, z′′	, z′′ .
xx	xy	yy	yx

We can differentiate a function as long as derivatives involved exist.

The derivatives z ′′ and z ′′ are called the mixed partial derivatives of the
xy	yx
second order and when they are continuous they are equal z′′			= z′′ .
		xy	yx
Example. Show, that z′′	= z′′	for given function
xy	yx

z = x 4 y 3 − 2x 2 y 5 + 8 .

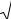
Solution.

′

z′′

= 12x 2 y 3 − 4 y 5

= 4x

− 4xy

z x

z′′

= 12x3 y 2 − 20xy 4

′

z′′

= 6x 4 y − 40x 2 y 3

= 3x

− 10x

z y

z′′

= 12x3 y 2 − 20xy 4

It is clear that

z′′

= z′′ .

Note that we can continue calculation of partial derivative of the third order, et cetera:

					z′′′
		z		′′			xxx
				xx		z′′′
	′						xxy
	′
z x					z′′′
					z′′′
			z	′′			xyx
			z	′′
				xy	z′′′
							xyy
z = z(x, y)					z′′′
					z′′′
				′′			yxx
			z yx
					z′′′
z	′						yxy
z	′				z′′′
	y				z′′′
				′′			yyx
		z yy
					z′′′
							yyy

In similar way we can find partial derivatives of the higher order of functions of three, four, …, n variables.

12. Differentiating Composite Functions

Let us consider a function z = z(x, y), where x = x(t ) and y = y(t ) are functions of one independent variable. Then formula for finding the derivative of composite function z = z(x, y) will be:

∂z

(12.1)

dt ∂x dt

∂y dt

Example. Find the derivative of the function

z =

and y = 5t .

ln y , where x = sin 2 t

Solution: Using the formula (12.1)

dz = ∂z dx + ∂z dy dt ∂x dt ∂y dt

we have

dz = ( x ln y)′ x (sin 2 t )′t + ( x ln y)′ y (5t )′t = dt

=	1		ln y2 sin t cos t +	x	5t ln 5.


2		x		y

13. Directional Derivative and Gradient of a Function of Several

Variables

An important characteristic of a function u = f (x, y, z) is the rate of its change in the given direction of a vector a = (a x ; a y ; a z ).

It is possible to prove that a directional derivative of the function u = f (x, y, z) at a point M 0 (x0 , y0 , z0 ) can be calculated by the formula

∂u(M 0 )

= u′ (M

)cosα + u′ (M

)cos β + u′

)cos γ

(13.1)

∂a

Here

cosα =

+ ay

+ az

cos β =

(13.2)

+ a

cosγ =

+ ay

+ az

Example 13.1. Find the directional derivative of the function z = 5xy − x 2 y 2 at a point M 0 (3;2) in the direction of the vector M 0 M1 , when the point M1 has coordinates (6; 6).

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.02.20163.53 Mб11Ekonom_inform_konspekt_zaoch.pdf
#
12.11.201969.63 Кб0electric current_прктик_раб.doc
#
10.02.20165.42 Mб9ELMAGN_lab_2_1-4_3_1-2.doc
#
10.02.20161.1 Mб27Filosofia.docx
#
10.02.201621.48 Кб13finansovaya_strategia_predpriatia_dlya_302.docx
#
10.02.20161.51 Mб19Functions of several variables- Textbook..pdf.pdf
#
10.02.20167.06 Mб22ga2ap.doc
#
10.02.201643.9 Mб39his_uk1.pdf
#
18.08.201940.66 Кб3INDIVIDUAL_NE_ZAVDANNYa_DO_TEMI_1.docx
#
10.02.2016684.03 Кб18ISDN Основные виды обслуживания.doc
#
31.08.201925.13 Mб2ISDN Основные виды обслуживания.doc

х2	+	у2	−	z 2	х2	+	у2	+	z2
а2	+		−	= 1	а2	+		+	= 1
а2		b2		c2	а2		b2		c2
					z
					b			z
				a	b
				a
		c						c
					y			c		y
					y				b

				x			a
				x			a
					x

х2	+	у2	−	z 2	х2	+	у2	+	z2
а2	+		−	= 1	а2	+		+	= 1
а2		b2		c2	а2		b2		c2
					z
					b			z
				a	b
				a
		c						c
					y			c		y
					y				b

				x			a
				x			a
					x

х2	+	у2	−	z 2	х2	+	у2	+	z2
а2	+		−	= 1	а2	+		+	= 1
а2		b2		c2	а2		b2		c2
					z
					b			z
				a	b
				a
		c						c
					y			c		y
					y				b

				x			a
				x			a
					x