
- •3 Изделия рэа на основе индуктивности
- •Классификация изделий рэа на основе индуктивности
- •Методики расчета индуктивности катушек
- •Резонансные катушки
- •Параметры резонансных катушек
- •Конструкции цилиндрических катушек
- •Катушки с сердечниками
- •Экранированные катушки
- •Индуктивно связанные катушки
- •Высокочастотные дроссели
- •3.4.1 Параметры высокочастотных дросселей
- •3.4.2 Основные конструкции высокочастотных дросселей
- •3.4.3 Условное обозначение и маркировка высокочастотных дросселей
- •Трансформаторы
- •Классификация трансформаторов
- •3.5.2 Система обозначения сердечников трансформаторов
- •3.5.3 Конструкции трансформаторов
- •Силовые трансформаторы
- •Согласующие трансформаторы
- •Импульсные трансформаторы
- •Экранирование трансформаторов
- •Дроссели низкой частоты
Методики расчета индуктивности катушек
Основным элементом катушек индуктивности является токовод. Величина индуктивности определяется конструкцией токовода и его размерами.
Полная индуктивность медного провода круглого сечения длиной lПРи диаметромd0равна
![]() (3.1)
(3.1)
Из (3.1) следует, что индуктивность провода уменьшается с ростом его диаметра. Это свойство широко используют в УКВ аппаратуре для уменьшения индуктивности соединительных проводов за счет увеличения их диаметра.
Если одиночный проводник согнуть, например, в кольцо, то его индуктивность уменьшится из-за встречного направления токов в соседних частях кольца. Однако, для круглого кольца индуктивность будет наибольшей по сравнению с индуктивностью витка любой другой конфигурации, поскольку круглый виток охватывает наибольшую площадь, обеспечивая наибольшее потокосцепление.
Индуктивность круглого плоского витка диаметром Dиз провода круглого сечения длинойlПРи диаметромdПРравна
![]() (3.2)
(3.2)
При сворачивании проводника в несколько витков wодинакового диаметра образуется катушка, индуктивность которой можно определить как суммарную индуктивность всех витков с учетом взаимоиндукцииMмежду ними:
![]() (3.3)
(3.3)
Индексы при Муказывают на взаимную индуктивность между первым и вторым, вторым и третьим, первым и третьим витками и т.д. Если известен коэффициент связи, который определяется равенством
![]() ,
(3.4)
,
(3.4)
то индуктивность катушки с произвольным числом витков определяется из
![]() . (3.5)
. (3.5)
Коэффициент связи между витками, расположенными на расстоянии τ, в однослойной катушке определяется выражением
 (3.6)
(3.6)
Для сплошной намотки τ=d0.
Индуктивность многослойной катушки незначительно зависит от диаметра провода, так как определяется в основном взаимоиндукцией между витками.
Из-за трудности определения коэффициента связи выражение (3.5) обычно применяют для расчета катушек индуктивности с небольшим числом витков (обычно не более шести).
Для катушек с однородным замкнутым магнитопроводом (с тороидальным сердечником) выражение для определения индуктивности принимает вид
![]() , (3.7)
, (3.7)
где μ– начальная магнитная проницаемость сердечника (μ=1 для диэлектрического каркаса или воздуха);
μ0=4π·10-7Гн/м – магнитная постоянная;
w– число витков обмотки;
S - площадь поперечного сечения катушки;
![]() - длина намотки катушки;
- длина намотки катушки;
Таким образом, увеличение индуктивности катушки может быть достигнуто за счет увеличения числа витков, магнитной проницаемости сердечника, площади поперечного сечения магнитопровода, а также уменьшения длины намотки.
В высокочастотных катушках замкнутый магнитопровод как правило отсутствует, поэтому индуктивность катушки будет меньше, рассчитанной по (3.7). Для учета рассеивания магнитного потока на краях катушки вводится поправочный коэффициент k, который зависит от отношения диаметра катушки к длине намотки
 (3.8)
(3.8)
Для практических расчетов однослойных цилиндрических катушек, намотанных виток к витку (рис.3.2 а),используют выражение
 , (3.9)
, (3.9)
где
 - коэффициент формы катушки, учитывающий
краевые эффекты;
- коэффициент формы катушки, учитывающий
краевые эффекты;
μ– начальная магнитная проницаемость сердечника (μ=1 для катушек без магнитного сердечника);
μ0=4π·10-7Гн/м – магнитная постоянная;
w– число витков обмотки;
![]() - площадь поперечного сечения круглой
катушки;
- площадь поперечного сечения круглой
катушки;
D– диаметр катушки;
![]() - длина намотки.
- длина намотки.
Для
практических расчетов однослойных
цилиндрических катушек без сердечника,
намотанных с принудительным шагом τ(рис.3.2 б),индуктивн ость
рассчитывают по (3.9), но полученный
результат уменьшают на поправкуΔL
ость
рассчитывают по (3.9), но полученный
результат уменьшают на поправкуΔL
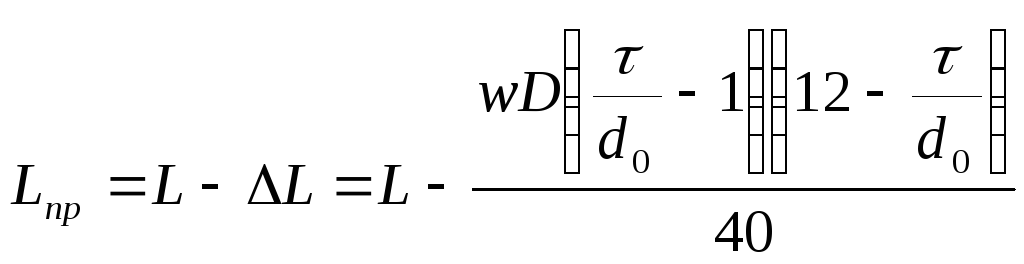 , (3.10)
, (3.10)
где τ– шаг намотки;
L– индуктивность катушки, определенная по (3.9) приμ=1.
Для практических расчетов индуктивности тороидальной однослойной катушки, намотанной сплошным слоем на круглом магнитном сердечнике прямоугольного сечения (рис.3.2 в), используют выражение
![]() , (3.11)
, (3.11)
где
![]() - площадь поперечного сечения сердечника
тороида;
- площадь поперечного сечения сердечника
тороида;
![]() - средняя длина сердечника тороида;
- средняя длина сердечника тороида;
D– внешний диаметр сердечника тороида;
d– внутренний диаметр сердечника тороида;
h– высота сердечника тороида.
Для практических расчетов многослойных катушек без сердечника(рис.3.2 г) используют выражение
 , (3.12)
, (3.12)
г деDCP
– средний диаметр катушки;
деDCP
– средний диаметр катушки;
t- толщина катушки;
l- длина катушки.
Для практических расчетов многослойных секционированных катушек без сердечника (рис.3.2 д) используют выражение
![]() , (3.13)
, (3.13)
где LC – индуктивность одной секции катушки;
n– число секций;
kCB– коэффициент связи между смежными
секциями, зависящий от отношения![]() (рис.3.3);
(рис.3.3);
b – расстояние между секциями.
Для практических расчетов плоских круглых спиральных катушек (рис.3.2 е) используют выражение
![]() , (3.14)
, (3.14)
где DBH,DH –внутренний и наружный диаметры катушки, соответственно.
Для практических расчетов плоских квадратных спиральных катушек (рис.3.2 ж) используют выражение
![]() , (3.15)
, (3.15)
где АBH,АH –внутренняя и наружная стороны катушки, соответственно.
