Теорема про зміну та збереження моменту імпульсу механічної системи

Вектор імпульсу (кількості руху) матеріальної системи характеризує її поступальний рух. Обертальний рух матеріальної системи характеризується іншим вектором - моментом імпульсу (кінетичним моментом). Для окремої матеріальної точки масою момент імпульсувідносно довільної точки просторувизначається виразом

, (1)

де - радіус-вектор проведений з точкидо матеріальної точки,- її імпульс. Векторзалежить від імпульсу та положення матеріальної точки відносно точкита характеризує її „обертальний” рух навколо точкив даний момент часу.

Векторний добуток можна обчислити за допомогою матриці

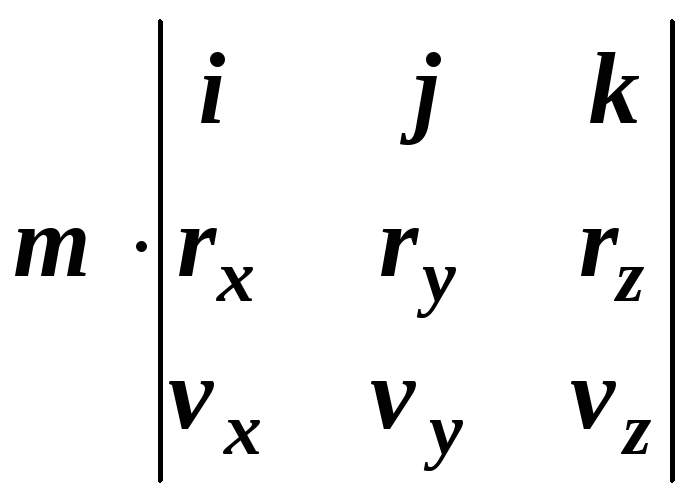=, (2)

де ,,та,,- проекції радіус-вектората швидкості точкина відповідні вісі. Таким чином, момент імпульсу матеріальної точки може бути знайдений за формулою

== (3)

= .

Проекції ,,вектора моменту імпульсу на декартові вісі,таназиваютьмоментом імпульсу матеріальної точки відносно осі.

Модуль і напрям вектора моменту імпульсу визначається за правилами векторного добутку. На рис. 3.1, зображена площина, в якій лежать векторита. Напрям моменту імпульсурухомої матеріальної точкивідносно точкиспрямований від нас перпендикулярно до площини рисунку, а його модуль можна знайти за формулою

. (4)

тут – кут між векторами і, а – відстань від точкидо лінії вздовж якої спрямована швидкість матеріальної точки.

Замість вектора моменту імпульсу матеріальної точки, часто користуються його алгебраїчним значенням, яке визначається за такими ж самими правилами, що і для визначення моменту сили відносно точки. Тоді для точки отримуємо

, (5)

а для точки (рис.1)

. (6)

Зауважимо: 1) у випадку прямолінійного рівномірного руху точки, її кінетичний момент відносно заданої точки простору залишається незмінним;

2) момент імпульсу матеріальної точки дорівнює нулю, якщо лінія вздовж якої спрямований вектор імпульсу проходить через цю точку.

Момент імпульсу механічної системи є векторною сумою моментів імпульсів (кінетичних моментів) її елементів

. (7)

Якщо тверде тіло обертається навколо фіксованої осі, то для знаходження моменту імпульсу, тіло розглядають як сукупність матеріальних точок масами , що знаходяться на незмінних відстаняхвід осі обертання і обертаються з однаковою для всіх точок кутовою швидкістю. Тоді момент імпульсу відносно осі обертання(дивись рис.2) можна обчислити як суму моментів імпульсу елементів тіла відносно неї

, (8)

що у випадку неперервного розподілу маси дає

, (9)

де – символ відповідної осі обертання. Сума добутків мас елементів на квадрат їхньої відстані до осі обертаннячи відповідний інтеграл по об’єму тіланазив.моментом інерції тіла відносно заданої осі

.(10)

Ця фізична величина характеризує інертність тіла при обертанні навколо заданої осі, залежить від розподілу маси в тілі, положення осі обертання і вимірюється в кг·м².

Для сукупності паралельних осей обертання момент інерції твердого тіла має мінімальне значення для осі, яка проходить через центр маси твердого тіла. Тоді для будь-якої іншої, паралельної до неї, момент інерції можна визначити за теоремою Гюйгенса-Штейнера

, (11)

де – маса тіла, а – відстань між центром маси тіла та віссю обертання.

Моменти інерції більшості однорідних тіл правильної форми відносно їх центру мас можна знайти у довідниках з фізики чи математики.

Похідна за часом від вектора моменту імпульсу механічної системи відносно даного центра дорівнює головному моментузовнішніх сил відносно того ж центра

. (12)

Формула (12) є математичним записом теореми про зміну моменту імпульсу механічної системи в диференціальній формі і називається також основним рівнянням обертального руху.

Векторне рівняння в проекціях на нерухомі вісі декартових координат еквівалентне трьом скалярним рівнянням

,,. (13)

З наведеної теореми випливають наступні наслідки:

1) внутрішні сили безпосередньо не впливають на зміну моменту імпульсу механічної системи (вони можуть здійснювати опосередкований вплив через зовнішні сили);

2) якщо головний момент зовнішніх сил відносно деякого нерухомого центру дорівнює нулю, то момент імпульсу механічної системи відносно того ж центра не змінюється. Дійсно, якщо , то з рівняння (12) матимемо

=, (14)

де – початкове значення вектора. Формула (3.14) є першим інтегралом рівняння руху системи і математичним записом закону збереження моменту імпульсу механічної системи;

3) якщо головний момент всіх зовнішніх сил не дорівнює нулю, але його момент відносно деякої вісі (наприклад, ) дорівнює нулю, то момент імпульсу механічної системи відносно цієї вісі не змінюється з часом. Дійсно з рівнянь (13) – (14) випливає, що коли, наприклад,, то

, (15)

тобто зберігається відповідний компонент моменту імпульсу механічної системи;

4) якщо момент зовнішніх сил відносно нерухомого центру не дорівнює нулю, то з рівняння (3.12) отримуємо

. (16)

Після інтегрування (3.16) в межах від початкового моменту часу до поточного, отримуємо

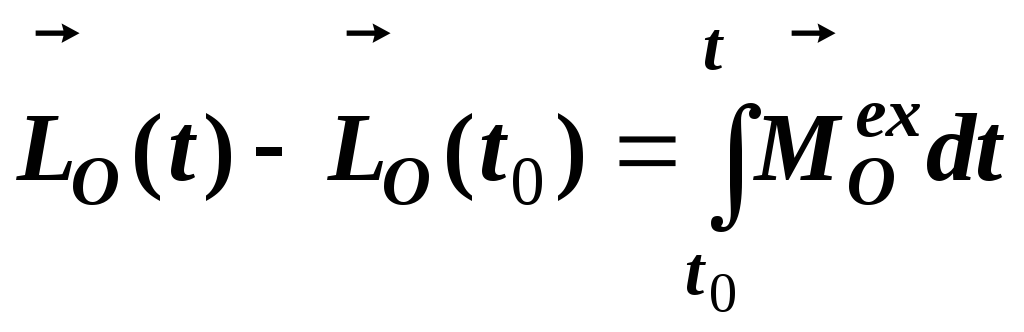, (17)

де – момент імпульсу механічної системи на поточний час, а– в момент часу. Таким чином,зміна моменту імпульсу механічної системи відносно нерухомого центру за проміжок часу віддодорівнює інтегралу від головного моменту імпульсу зовнішніх сил по часу за той самий проміжок часу.