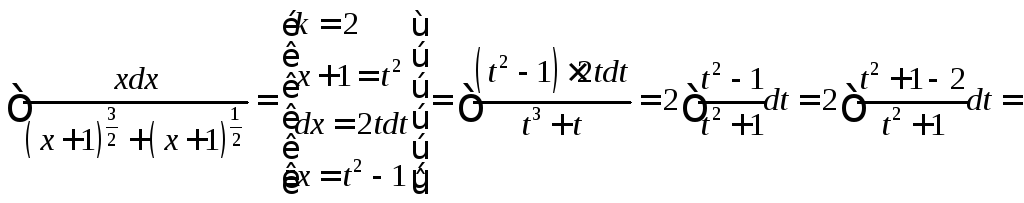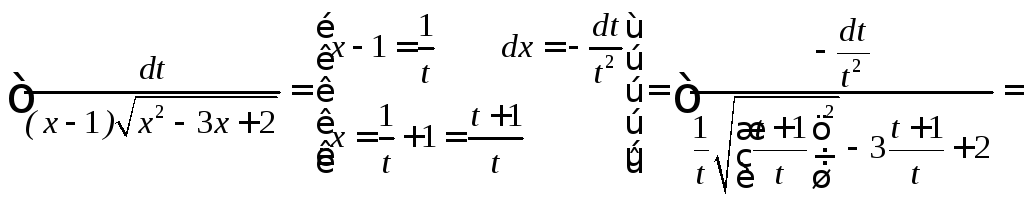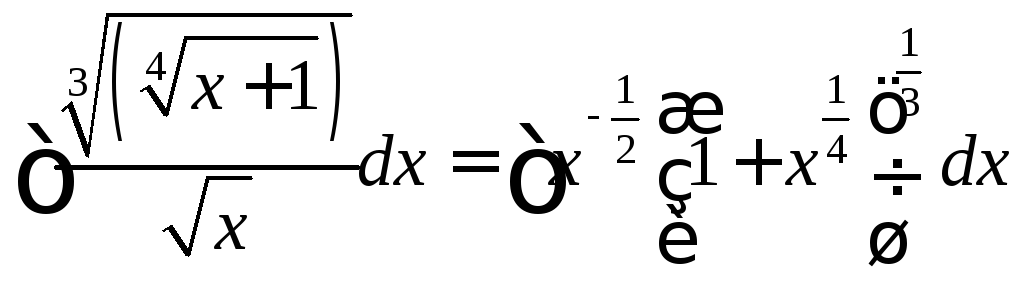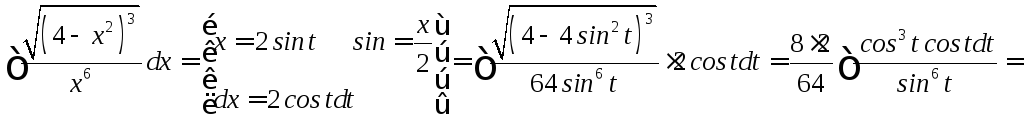- •Высшая математика конспект лекций
- •1 Курс, 2 семестр
- •Содержание
- •Тема 6 «Функции нескольких переменных» 7
- •Тема 7 «Комплексные числа. Многочлены» 13
- •Тема 8 «Неопределённый интеграл» 19
- •Тема 9 «Определенный интеграл» 38
- •Тема 10 «Приложения определенного интеграла» 43
- •Тема 11 «Дифференциальные уравнения» 48
- •Введение
- •Тематический план
- •Предел функции двух переменных.
- •Частные производные первого порядка
- •Градиент функции. Производная по направлению вектора.
- •Вопросы для самоконтроля
- •Тема 7 «Комплексные числа. Многочлены» Основные понятия
- •Действия с комплексными числами
- •Рациональные дроби. Краткие сведения из теории многочленов.
- •Рациональные дроби.
- •Вопросы для самоконтроля
- •Тема 8 «Неопределённый интеграл» Первообразная функция. Основная теорема о первообразных
- •Понятие неопределенного интеграла
- •Основные свойства неопределенного интеграла
- •Инвариантность формул интегрирования
- •Метод непосредственного интегрирования
- •Метод замены переменной (способ подстановки)
- •Интегрирование по частям
- •Интегралы от некоторых функций, содержащих квадратный трехчлен
- •Интегрирования рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование иррациональных функций
- •Интегралы от дифференциальных биномов
- •Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
- •Вопросы для самоконтроля
- •Тема 9 «Определенный интеграл» Понятие определённого интеграла.
- •Основные свойства определённого интеграла.
- •Вопросы для самоконтроля
- •Тема 10 «Приложения определенного интеграла» Вычисление площадей плоских фигур
- •Вычисление объема тела
- •Обыкновенные дифференциальные уравнения 1-го порядка.
- •Условие (5) называется начальным условием.
- •Дифференциальные уравнения с разделяющимися переменными.
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •Нетрудно заметить, что уравнение (21) представляет собой уравнение с разделяющимися переменными, метод решения которого изложен в лекции 1.
- •Уравнение Бернулли Уравнением Бернулли называется уравнение вида:
- •Геометрические задачи.
- •Пример 7.
- •Решение
- •Дифференциальные уравнения высших порядков.
- •Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •Решить дифференциальное уравнение:
- •Пример 10.
- •Линейные дифференциальные уравнения порядка n
- •Решение линейных неоднородных уравнений
- •Решение однородных уравнений.
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.
- •Укажем частные решения , соответствующие различным простейшим случаям специальной правой части:
- •Пример. (Задача типа 61-70).
- •Решение
- •Вопросы для самоконтроля
- •Литература
Интегрирование иррациональных функций
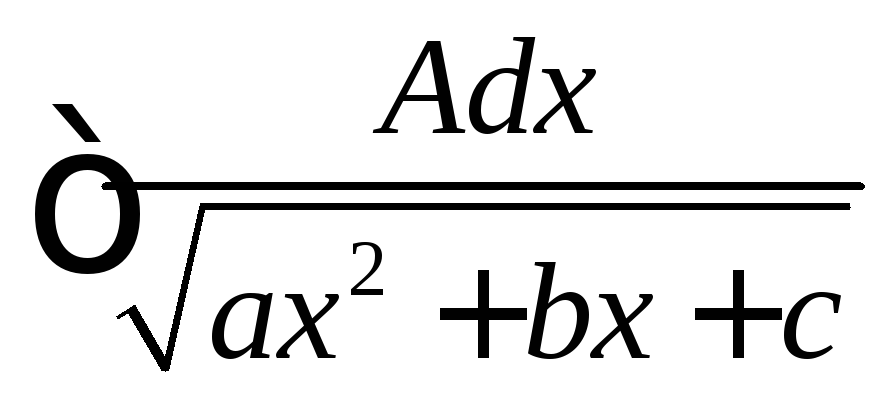 выделяем
полный квадрат и делаем замену
выделяем
полный квадрат и делаем замену
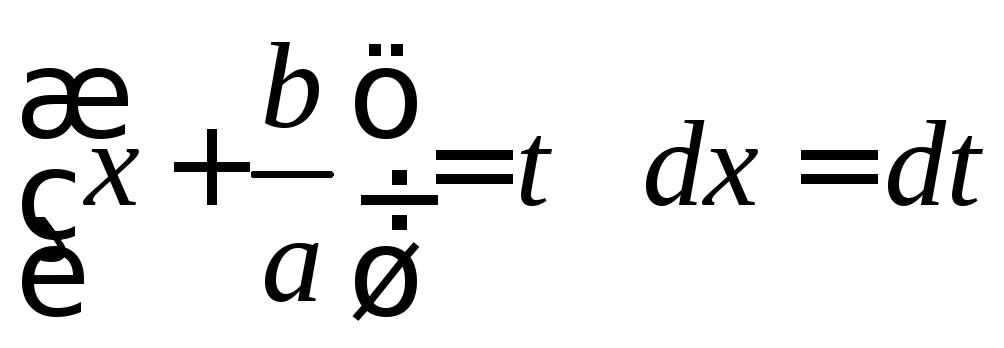 (см § 10) интеграл I1
искомый интеграл сводится к виду
(см § 10) интеграл I1
искомый интеграл сводится к виду
![]() (ф-ла
20) и
(ф-ла
20) и
![]() (ф-ла 17)
(ф-ла 17)
Пример
1)
![]() выделим полный квадрат
выделим полный квадрат
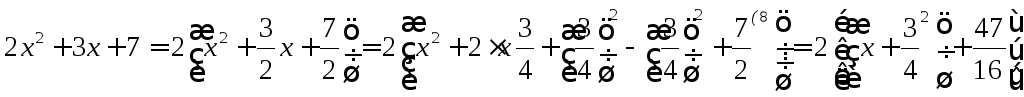
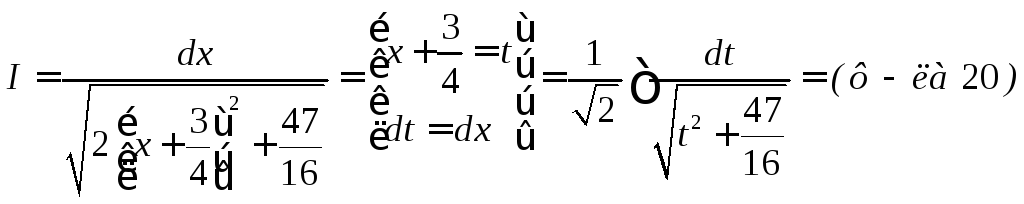
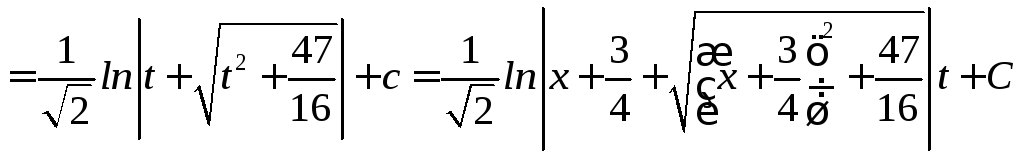
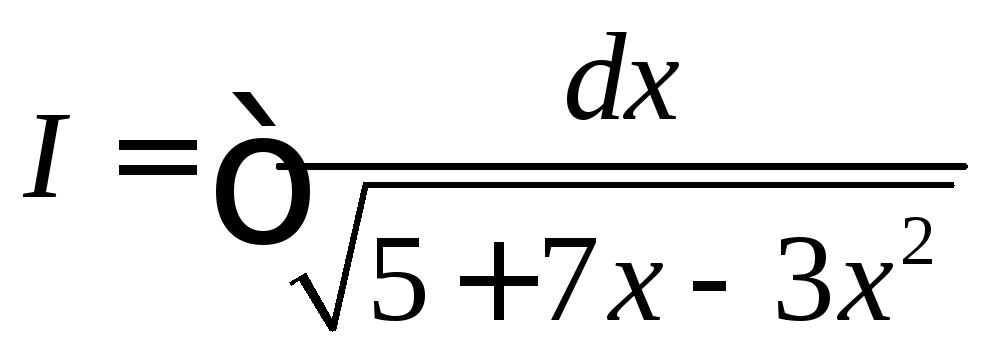 выделяем
полный квадрат:
выделяем
полный квадрат:
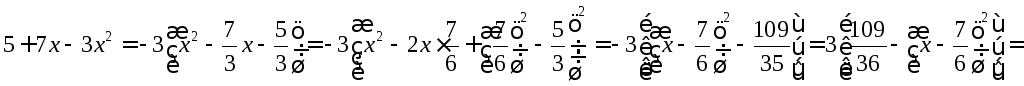
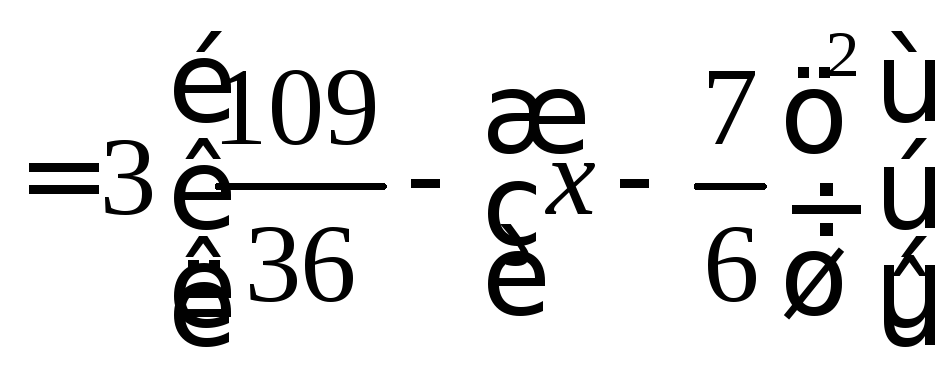
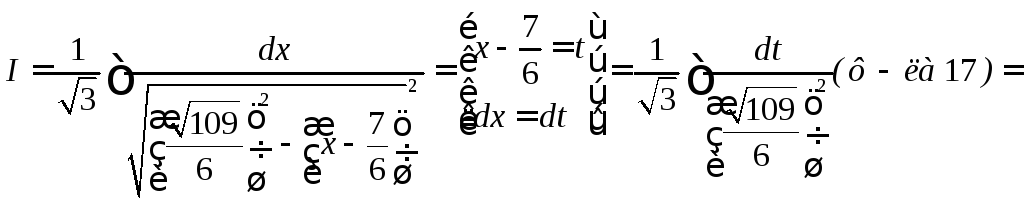
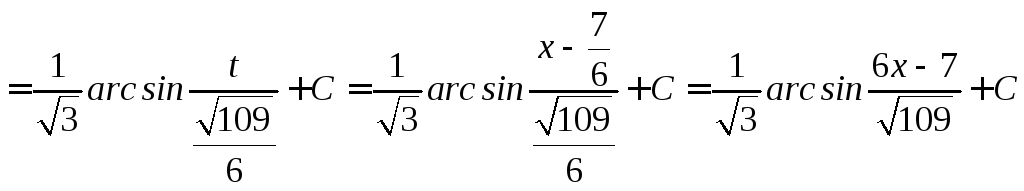
II
![]() делаем так, чтобы в числителе была
производная знаменателя и разбиваем
на два интеграла
делаем так, чтобы в числителе была
производная знаменателя и разбиваем
на два интеграла
![]()
Выделим полный квадрат
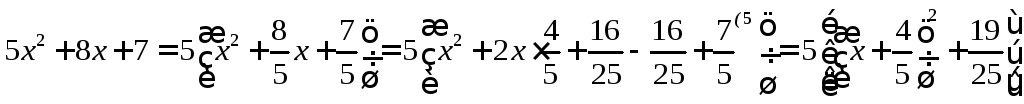
Итак
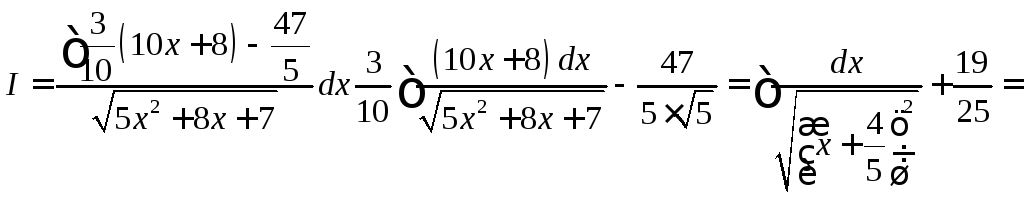
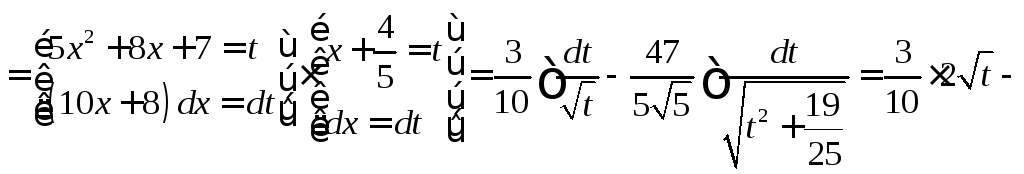
ф-ла ф-ла 20
2а 20
-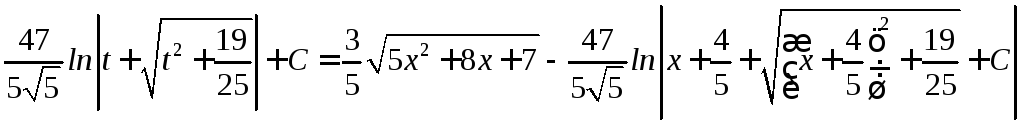
III.
Интегралы вида
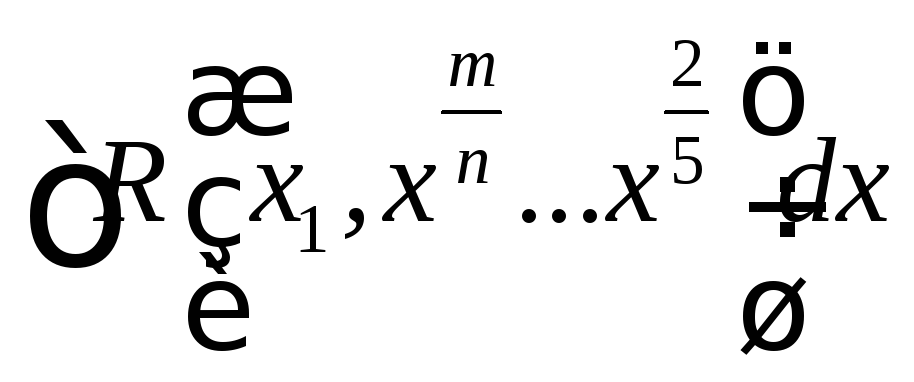 ,
где R
рациональная функция своих аргументов.
,
где R
рациональная функция своих аргументов.
Пусть k наименьший общий знаменатель дробей
![]() подстановка
подстановка
![]()
Тогда каждая дробная степень х выражается через целую степень t и, следовательно, подынтегральная функция преобразуется в рациональную степень t
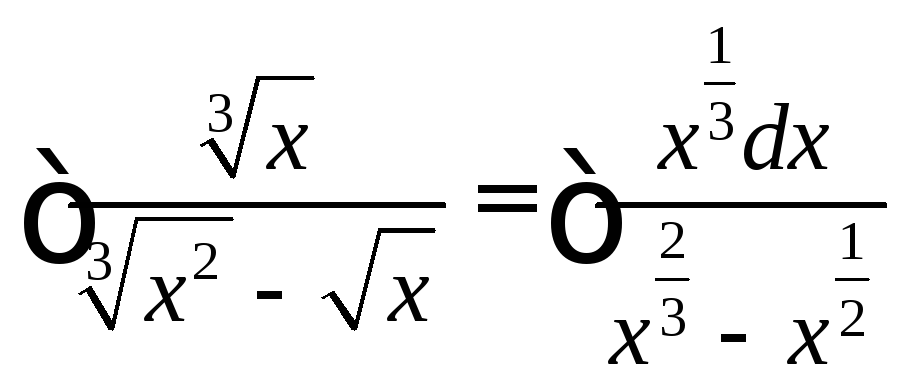 наименьшим
общим знаменателем дробей
наименьшим
общим знаменателем дробей
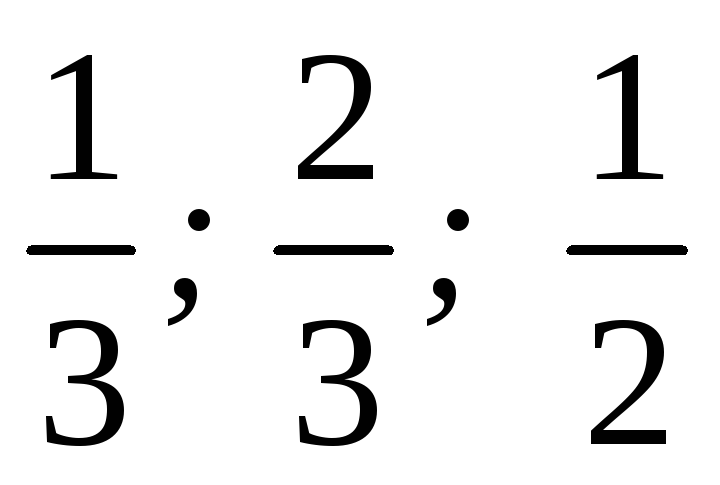 является число 6, поэтому замена
является число 6, поэтому замена
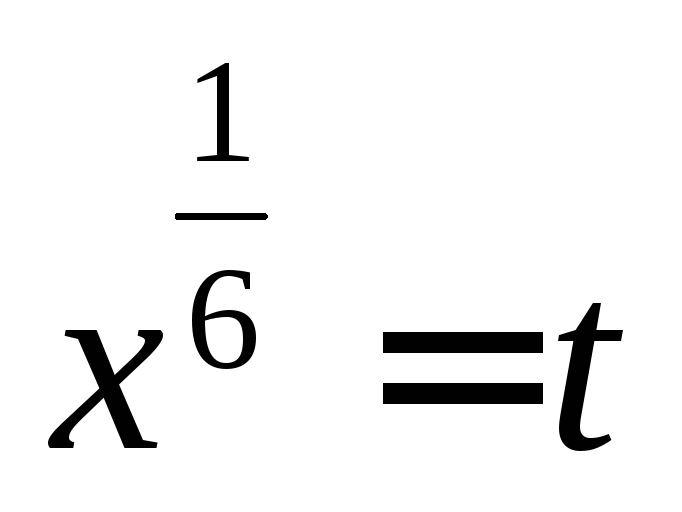
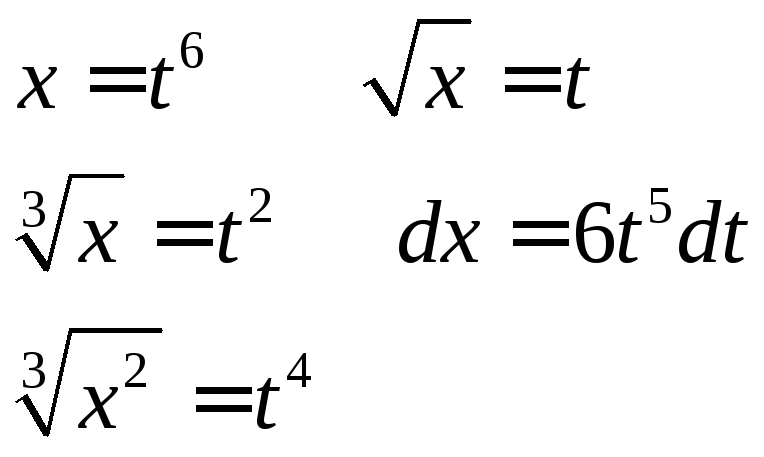
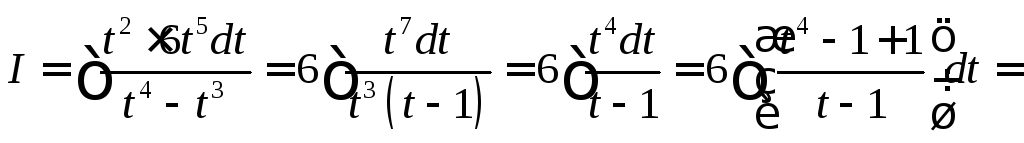
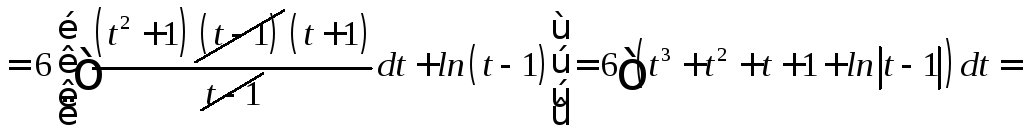
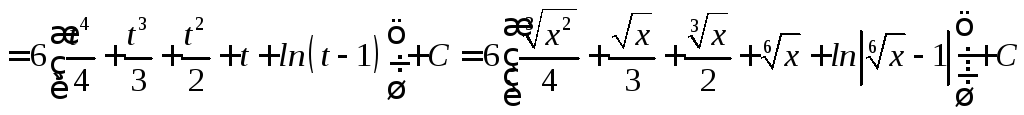
IV.
Интегралы вида
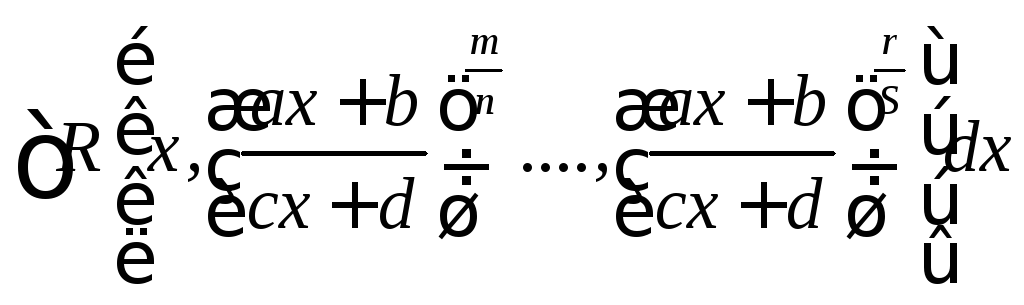
Пусть
k
– наименьший общий знаменатель дробей
![]() ,
тогда
,
тогда
![]()
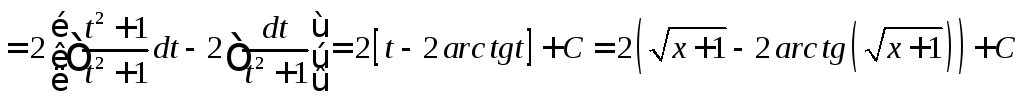
Интегралы вида
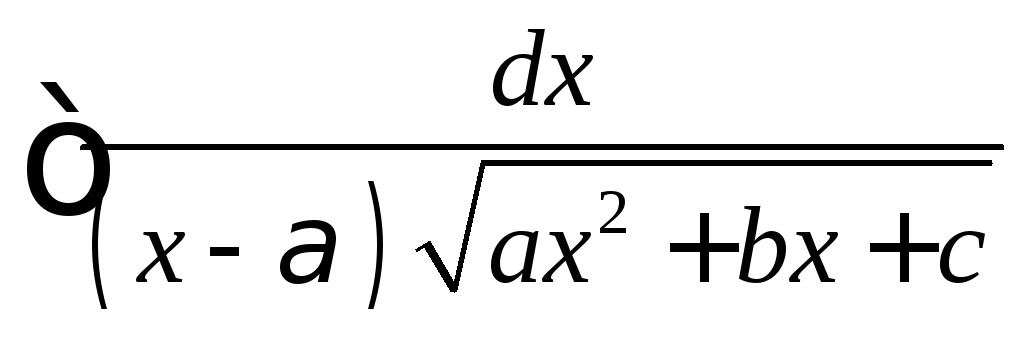 заменой
заменой
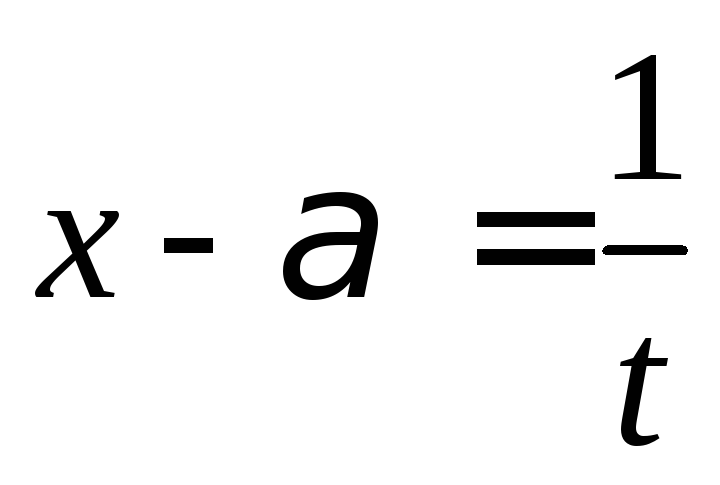 сводится к виду
сводится к виду
![]()
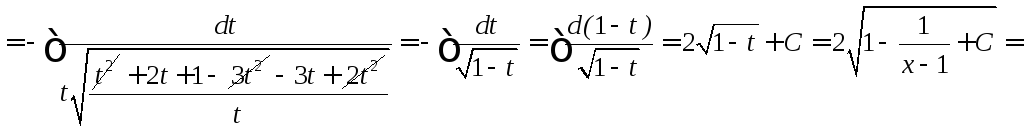
![]()
Интегралы от дифференциальных биномов
![]() ,
где m,
n,
p,
- рациональные числа
,
где m,
n,
p,
- рациональные числа
П.А. Чебышев доказал, что этот интеграл выражается через конечную комбинацию элементарных функций в следующих трех случаях
1)
р – целое
![]() где k
– наименьший общий знаменатель дробей
m
и n
где k
– наименьший общий знаменатель дробей
m
и n
2)
![]() - целое или равно 0 подстановка
- целое или равно 0 подстановка
![]() где S
– знаменатель дроби р
где S
– знаменатель дроби р
3)
![]() - целое или 0 подстановка
- целое или 0 подстановка![]()
S знаменатель р
 (случай
2)
(случай
2)
Подстановка
![]()
![]()
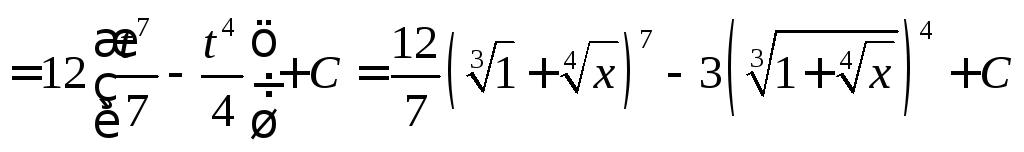
Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
![]()
![]()
![]()
![]()
Вернемся к старой переменной. Нам надо выразить ctgt через sint. Воспользуемся формулой:
![]() отсюда
отсюда
![]()
Итак
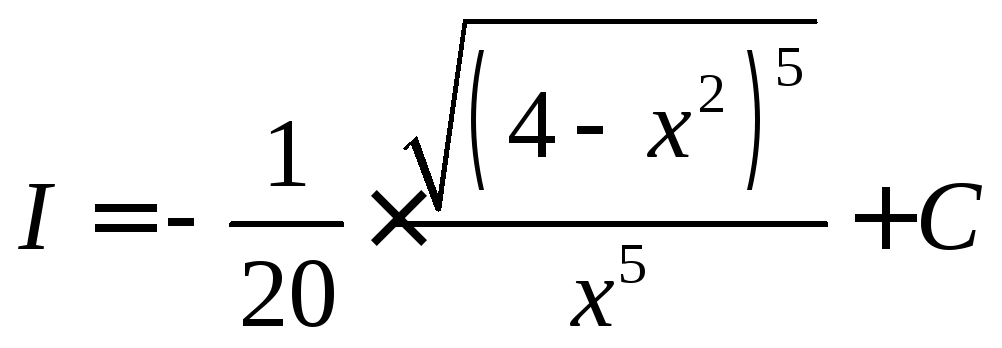
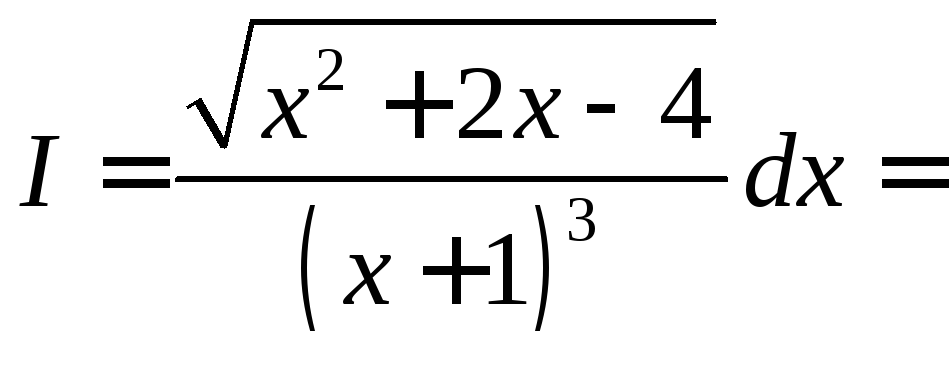 выделяем
в числители полный квадрат
выделяем
в числители полный квадрат
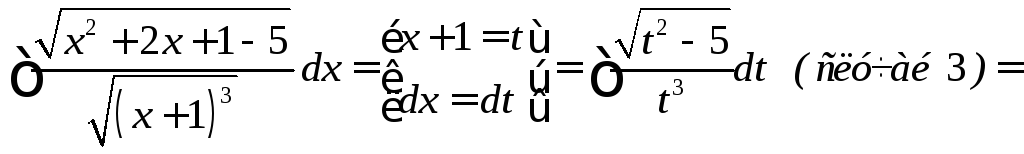
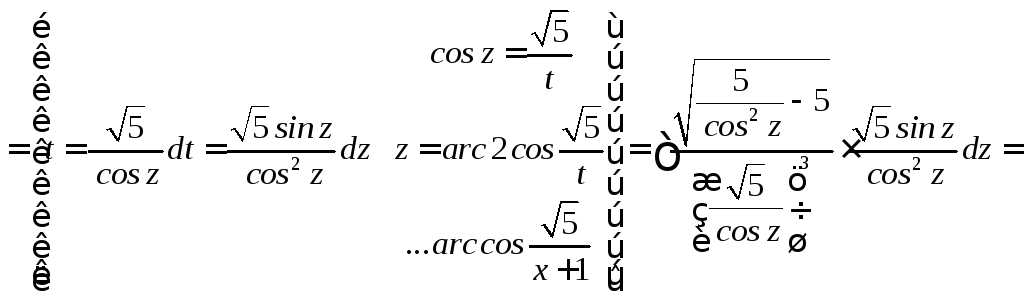
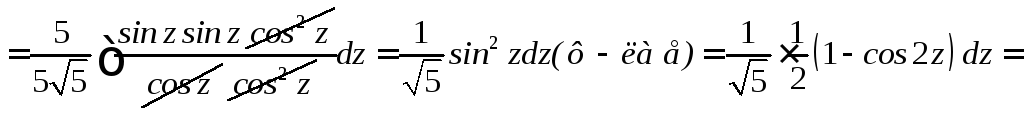
![]()
Перейдем к старой переменной
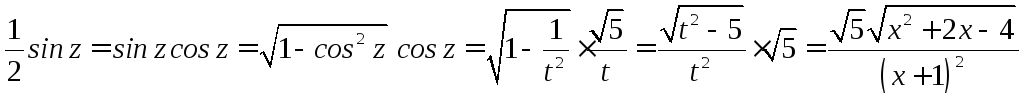
Итак
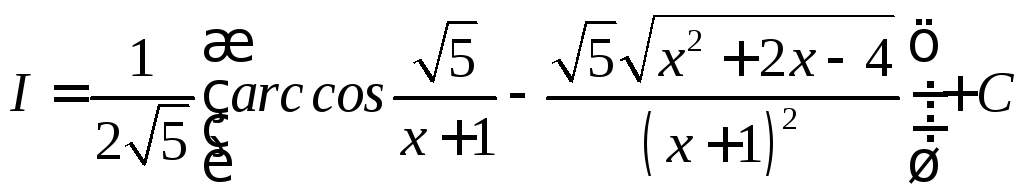
Вопросы для самоконтроля
Первообразная функция. Основные теоремы о первообразных.
Понятие неопределенного интеграла.
Теорема о производной от неопределенного интеграла.
Теорема о дифференциале от неопределенного интеграла.
Теорема о неопределенном интеграле от дифференциала.
Доказать, что постоянный множитель можно выносить за знак неопределенного интеграла.
Теорема о неопределенном интеграле от алгебраической суммы конечного числа функций.
Метод замены переменной (внесение под знак дифференциала).
Интегрирование по частям неопределенного интеграла.
Интеграл вида
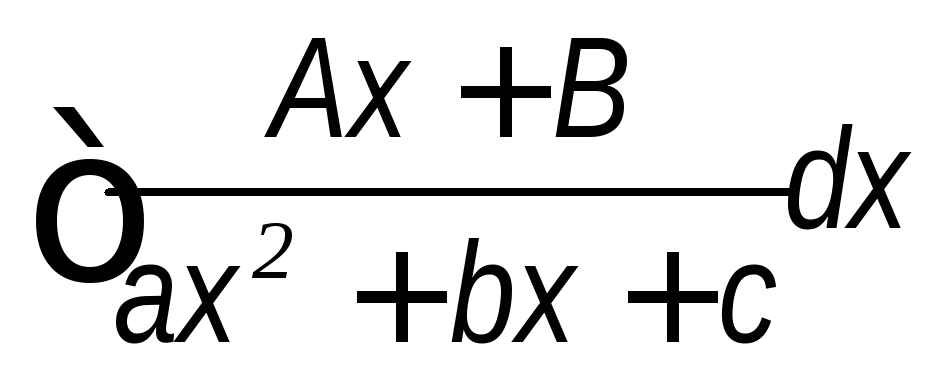 .
.Схема разложения алгебраических дробей на элементарные.
Интегралы вида
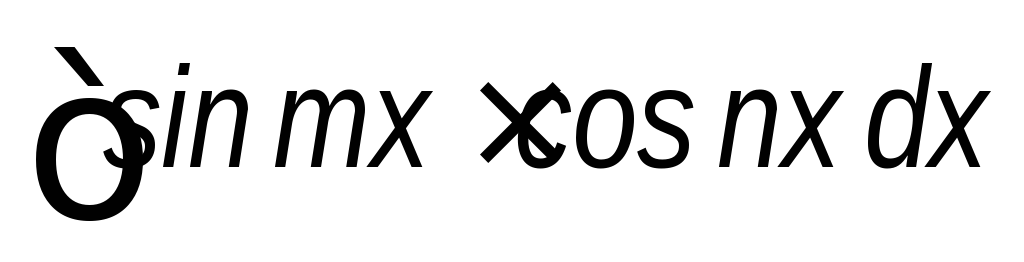 ;
;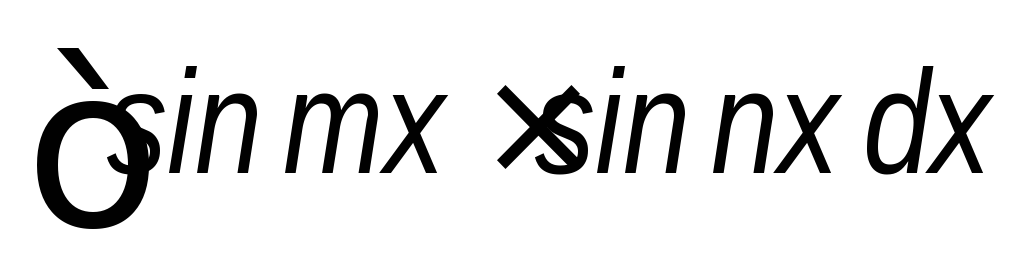 ;
;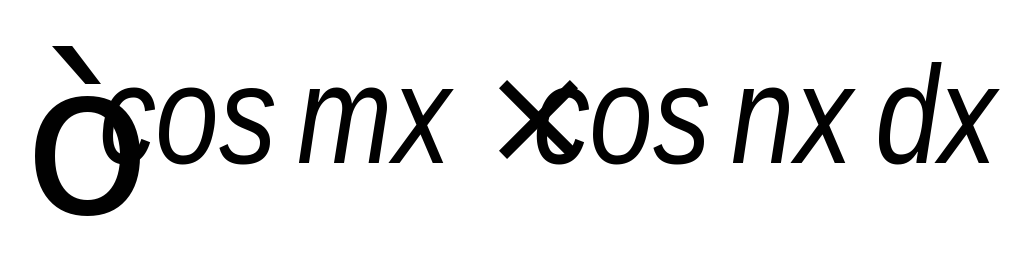 .
.Интегралы вида
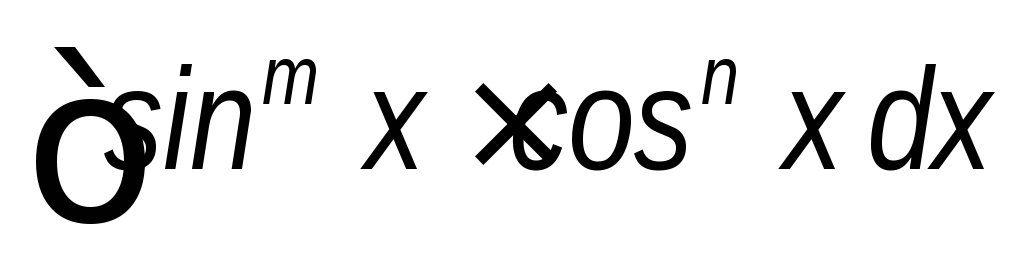 (m>0,
n>0,
хотя бы одно из них нечетное).
(m>0,
n>0,
хотя бы одно из них нечетное).Интегралы виды
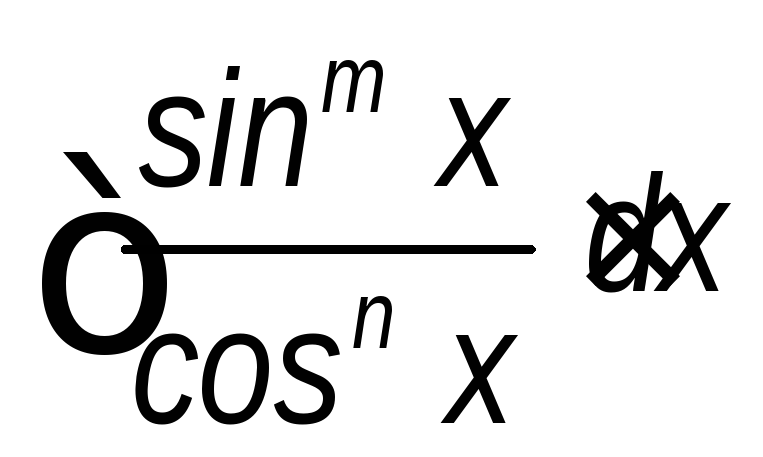 ;
;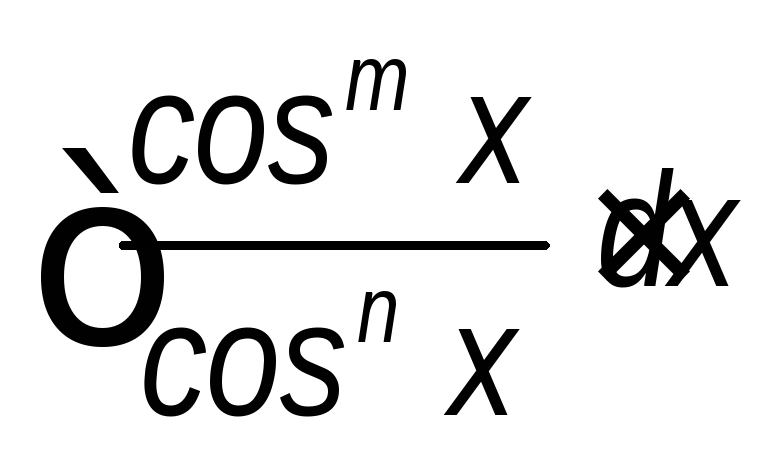 (m – нечетное).
(m – нечетное).Интегралы вида
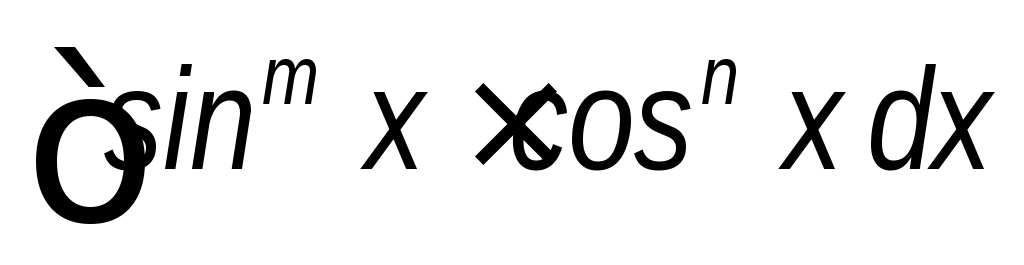 (m>0,
n>0,
оба четные).
(m>0,
n>0,
оба четные).Интегралы вида
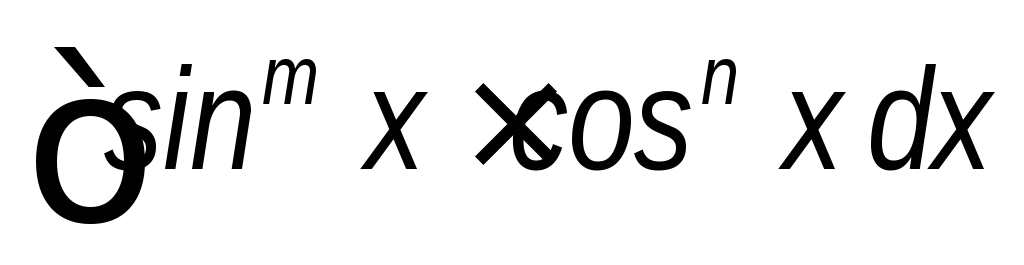 (m>0,
n<0,
оба четные);
(m>0,
n<0,
оба четные);
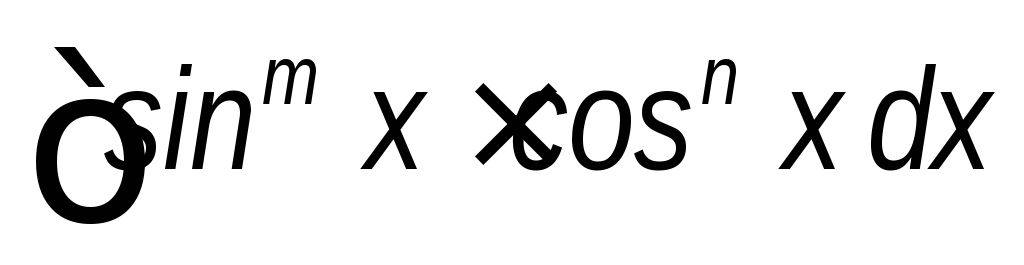 (m
и n
нечетные, одно из них отрицательное);
(m
и n
нечетные, одно из них отрицательное);
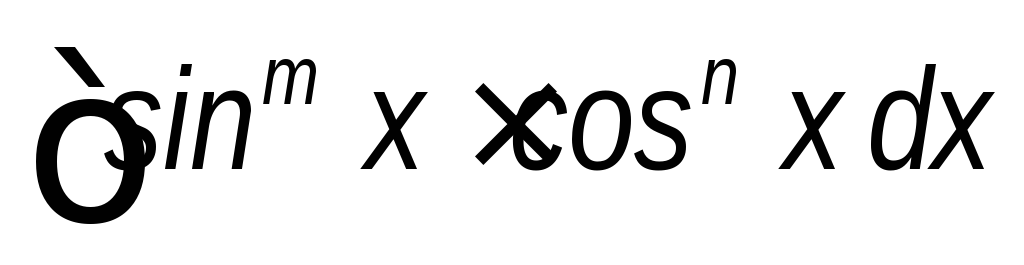 (m
и n
отрицательные, их сумма четное число).
(m
и n
отрицательные, их сумма четное число).Интегралы вида
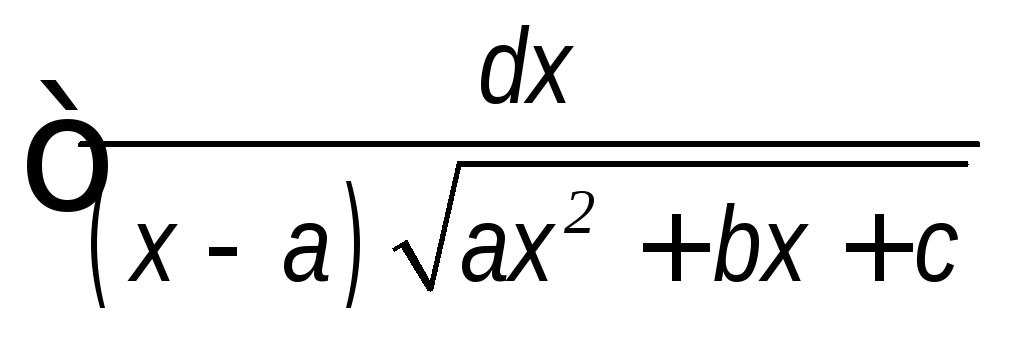 .
.Интегрирование иррациональных выражений с помощью тригонометрических подстановок.
Тема 9 «Определенный интеграл» Понятие определённого интеграла.
Пусть
на отрезке
![]() задана функция
задана функция
![]() .
Рассмотрим фигуру (см. рис. 1), ограниченную
графиком функции
.
Рассмотрим фигуру (см. рис. 1), ограниченную
графиком функции
![]() ,
прямыми
,
прямыми
![]() ,
,
![]() и осью
и осью
![]() .
Её
называют криволинейной
трапецией.
Поставим
задачу об определении и вычислении
площади этой криволинейной трапеции.
.
Её
называют криволинейной
трапецией.
Поставим
задачу об определении и вычислении
площади этой криволинейной трапеции.
Отрезок
![]() разобьём на n
произвольных
частей точками:
разобьём на n
произвольных
частей точками:
![]() .
.
Через
точки
![]() проведём
прямые, параллельные оси
проведём
прямые, параллельные оси
![]() .
Криволинейная
трапеция разобьется на n
частичных
криволинейных трапеций. Теперь на
каждом из отрезков
.
Криволинейная
трапеция разобьется на n
частичных
криволинейных трапеций. Теперь на
каждом из отрезков
![]() ,
,
![]() ,
…,
,
…,
![]() произвольно выберем по точке
произвольно выберем по точке
![]() ,
,
![]()
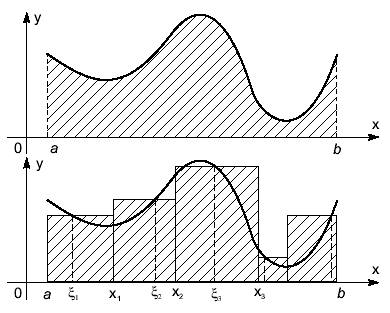
Рис. 1. Нахождение площади криволинейной трапеции
Вычислим
значение
![]() .
И каждую частичную криволинейную
трапецию заменим прямоугольниками с
высотами
.
И каждую частичную криволинейную
трапецию заменим прямоугольниками с
высотами
![]() ,
,
![]() ,
...,
,
...,
![]() .
Тогда можно полагать, что для площади
.
Тогда можно полагать, что для площади
![]() криволинейной трапеции справедливо
соотношение
криволинейной трапеции справедливо
соотношение
![]() .
.
Естественно предположить, что это равенство будет тем точнее, чем меньше максимум длин отрезков разбиения
![]()
Поэтому
площадь криволинейной трапеции
![]() равна
равна
![]() (1)
(1)
Число
S,
равное
пределу (1), называют определенным
интегралом от
функции
![]() по отрезку
по отрезку
![]() и обозначают
и обозначают
![]()
Таким образом, задача о вычислении площади криволинейной трапеции приводит к введению понятия определённого интеграла.