Тематический план

Тема 6 «Функции нескольких переменных»

Функции нескольких переменных. Частные производные. Оценка погрешности с помощью дифференциала. Градиент. Метод наименьших квадратов.

Тема 7 «Комплексные числа. Многочлены»

Понятие комплексного числа. Действия с комплексными числами. Алгебраическая, тригонометрическая, показательная формы комплексного числа. Разложение многочлена на множители.

Тема 8 «Неопределённый интеграл»

Понятие неопределенного интеграла. Табличные интегралы. Основные методы интегрирования разных классов элементарных функций.

Тема 9 «Определенный интеграл»

Определенный интеграл. Основные свойства. Формула Ньютона-Лейбница. Несобственные интегралы.

Тема 10 «Приложения определенного интеграла»

Вычисление площадей, объемов тел вращения, длины дуги кривой. Физические приложения определенного интеграла.

Тема 11 «Дифференциальные уравнения»

Дифференциальные уравнения 1-го порядка (с разделяющимися переменными, однородные и линейные). Уравнения 2-го порядка, допускающие понижение порядка. Линейные однородные и неоднородные уравнения 2-го порядка с постоянными коэффициентами. Дифференциальные уравнения механических колебаний.

Тема 6 «Функции нескольких переменных»

Основные понятия

Если каждой паре чисел и , называемых независимыми переменными, однозначно соответствует число у, называемое зависимой переменной, то говорят, что у есть функция двух переменных: тогда записывают:

.

Функции двух и более независимых переменных находят широкое применение в экономике. Приведем примеры лишь некоторых из них:

1. Издержки производства у являются функцией материальных затрат и расходов на оплату рабочей силы :

.

2. Производительность труда у является функцией от уровня квалификации и уровня автоматизации труда .

3. Спрос на товар у является функцией цены товара и средней заработной платы .

В трехмерном пространстве оси координат обозначают через Ox, Оу, Oz. Поэтому функцию двух переменных часто записывают и так:

.

Такая запись удобна для геометрического ее изображения. Например, графическое представление (рис. 8) функции

есть плоскость, проходящая через точки .

А геометрическое изображение (рис. 8) функции

д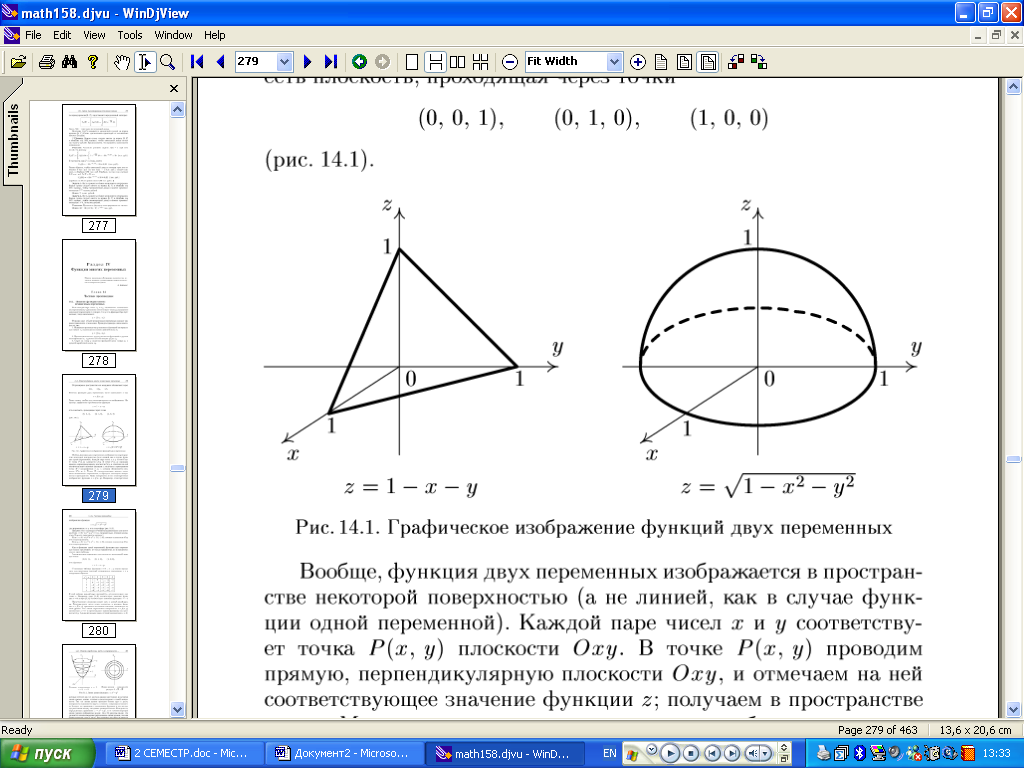ля переменныхх и у есть полусфера

Рис. 8. Графическое изображение функций двух переменных

Представление о функции может дать и метод линий уровня. Геометрическое место точек плоскости, в которых функция принимает постоянное значение, называется линией уровня. Это линия пересечения поверхности плоскостью и ортогонально спроектированная на плоскость Оху. Сделав несколько таких сечений плоскостями , которые отстоят друг от друга на равное расстояние, и вычертив линии уровня, можно составить представление о самой поверхности. Там где линии уровня проходят близко друг к другу, поверхность поднимается круто, а значит, и функция изменяется быстрее по сравнению с изменением функции в тех местах, где расстояние между соседними линиями больше.

Поверхность, определяемая уравнением

,

и ее соответствующие линии уровня изображены на рис. Из рисунка видно: чем дальше от начала координат расположены линии уровня, тем они ближе подходят друг к другу. Это означает, что при удалении от начала координат поверхность поднимается все круче. Обратно, чем ближе к началу координат, тем медленнее меняется функция.

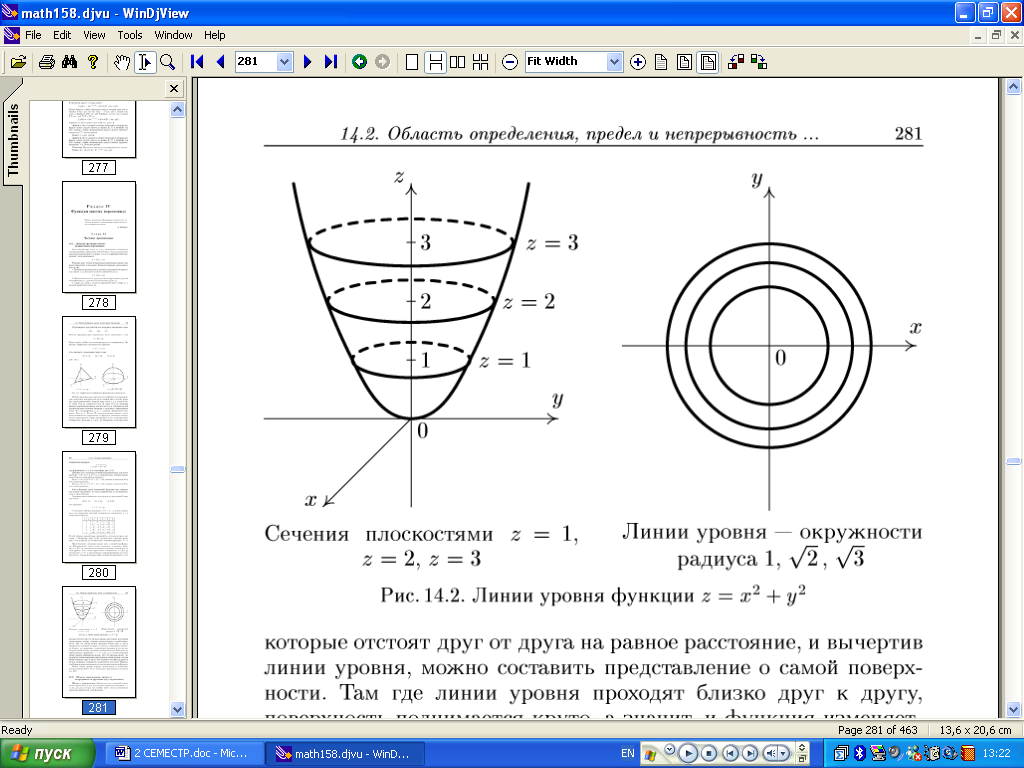
Сечения плоскостями Линии уровня окружности

радиуса

Рис. 9. Линии уровня функции

Множество всех значений независимых переменных х и у, для которых определена функция (для которых она вообще имеет смысл), называется областью определения этой функции.

Например, область определения функции

есть вся плоскость Оху, так как соответствующая формула имеет смысл при всех значениях х и у.

Формула

имеет смысл только при тех действительных х и у, при которых

.

Поэтому соответствующая функция определена лишь в круге

.