Дифференциальные уравнения высших порядков, допускающие понижение порядка
Некоторые
дифференциальные уравнения удается
решить, предварительно понизив их
порядок. К классу таких дифференциальных
уравнений относят так называемые
неполные (отсутствуют либо х, либо у)
дифференциальные уравнения вида:
Рассмотрим каждый из этих случаев в отдельности.
Уравнения вида
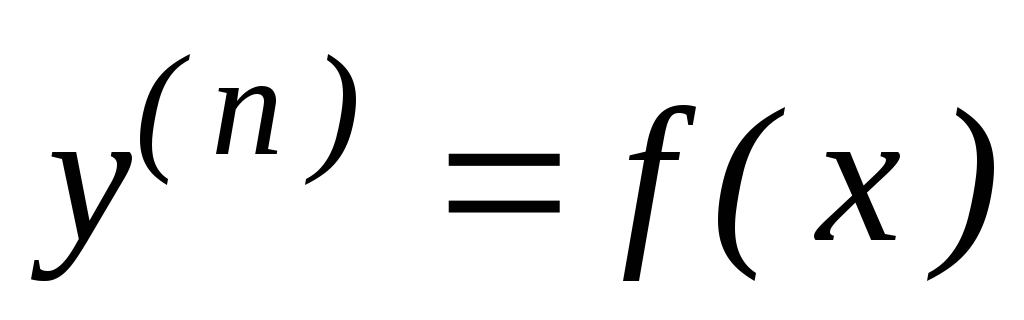(45)
Решение
этого уравнения находится n
– кратным интегрированием. По
определению производной имеем:
…, …, ….
.
Тогда
уравнение (45) принимает вид:
откуда
(46)
Уравнение
(46) представляет собой уравнение 1-го
порядка относительно неизвестной
функции у(n-1)
c
разделяющимися переменными, интегрируя
которое, получаем:
где
С1
= const
где
(47)
Полученное
уравнение (47) – это уравнение (n
– 1) – го порядка такого же типа, что и
(45). Применив к уравнению (47) описанный
выше метод понижения порядка, будем
иметь:
;
;
;
где С2
= const
(48)
К уравнению (48) опять применим изложенный выше метод и так до тех пор, пока, постепенно понижая порядок, не дойдем до искомой функции у.
Пример 8. Найти частное решение дифференциального уравнения
,
(49)
удовлетворяющее
начальным условиям:
;
;
.
(50)
Решение.
Разделив обе части уравнения (49) на х3
(в предположении, что х3
≠ 0), получаем:
(51)
Уравнение (51) представляет собой дифференциальное уравнение 3 – го порядка, относящееся к типу (45).
Сначала
найдем его общее решение последовательным
интегрированием (учитывая, что
).
где
С1
= const;
С1
;
;
,
где
;
;
;
где
;
.
(52)
Формула (52) определяет общее решение уравнения (51). Для определения значений произвольных постоянных С1, С2, С3, соответствующих искомому частному решению уравнения (49), воспользуемся начальными условиями (50):
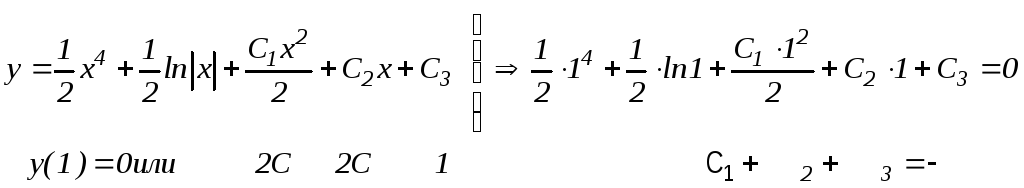
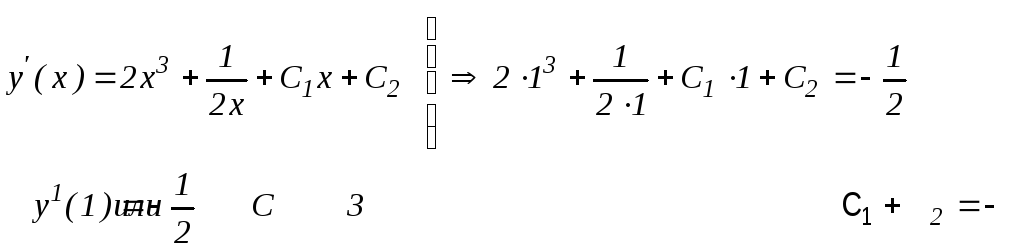
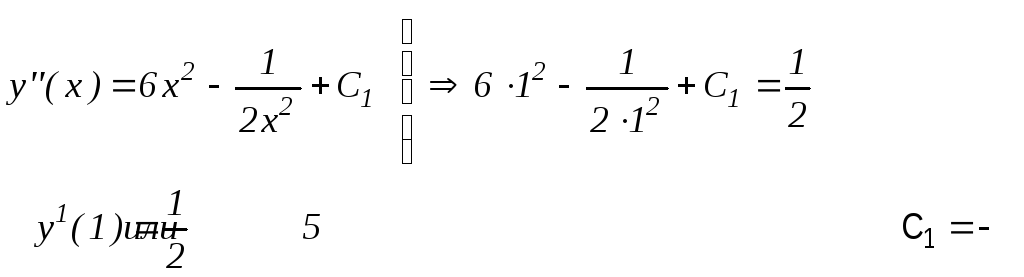
Таким
образом, имеем систему:
,
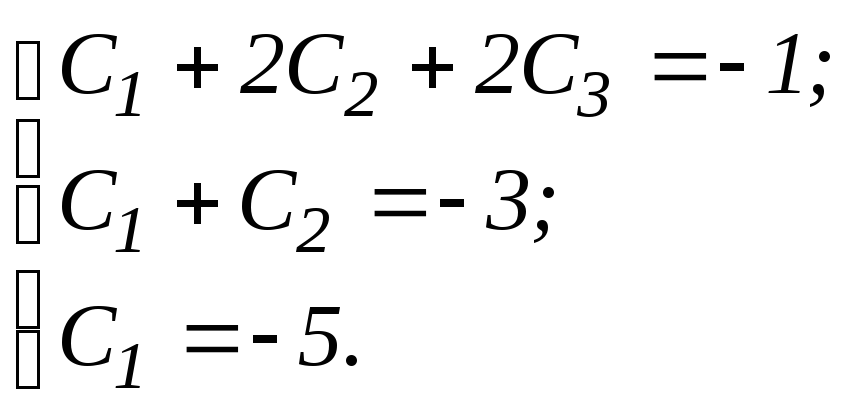решая которую, находим: С1
= -5, С2
= 2, С3
= 0.
Подставив найденные выше значения произвольных постоянных С1, С2, С3 в общее решение (52), получаем искомое частное решение заданного уравнения (49):
Ответ:
.
2.
Уравнение вида
(53)
Характерная особенность уравнения (53) заключается в том, что оно не содержит в явном виде искомую функцию у и ряд её низших производных.
Порядок такого уравнения можно понизить на k единиц с помощью замены уk = z (т.е. приняв за новую неизвестную функцию z (x) – низшую из производных данного уравнения). В результате (с учетом того, что из уk = z (х) следует у(k+1) = z/(х),, у(k+2) = (у(k+1))/ = (z/(х))/= z||(х),…, y(n) = y(k+(n-k)) = z (х)(n-k)) получаем уравнение (n – k) – го порядка: F (x, z, z’, z||,…z(n-k)) = 0 (54)
Пример 9.