
M00685(В.М
.).pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ Запорізький національний технічний університет
МЕТОДИЧНІ ВКАЗІВКИ
до виконання контрольних робіт та самостійної роботи студентів факультетів
радіоприладобудівного та інформатики і обчислювальної техніки денної та заочної форми навчання
за темами
“ТЕОРІЯ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ.
ОПЕРАЦІЙНЕ ЧИСЛЕННЯ”
2005
2
Методичні вказівки до виконання контрольних робіт та самостійної роботи студентів факультетів радіоприладобудівного та інформатики і обчислювальної техніки денної та заочної форми навчання за темами “Теорія функцій комплексної змінної. Операційне числення” /Укл.: Т. І. Левицька, Г.А. Шишканова, І. С. Пожуєва. – Запоріжжя: ЗНТУ, 2005. – 68 с.
Укладачі: Т. І. Левицька, доцент, к.т.н. Г.А. Шишканова, ст. викл. І. С. Пожуєва, доцент, к.т.н.
Експерт спеціальності: В.С. Кабак, доцент, к.т.н.
Рецензент: Ю. В. Мастиновський, доцент, к.т.н.
Відповідальний за випуск: Т. І. Левицька, доцент, к.т.н.
Затверджено радою РП факультета |
Затверджено на засіданні |
|
кафедри прикладної математики |
||
ЗНТУ |
ЗНТУ |
|
Протокол № 5 від 03.02.05 |
||
|
||
|
Протокол № 4 від 07.12.04 |
3
ЗМІСТ
Вступ............................................................................................................ |
|
4 |
1 ТЕОРІЯ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ....................... |
5 |
|
1.1 |
Комплексні числа та дії над ними ............................................. |
5 |
1.2 |
Основні елементарні функції комплексної змінної............... |
10 |
1.3 |
Аналітичні функції.................................................................... |
13 |
1.4 |
Інтегрування функції комплексної змінної ............................ |
14 |
1.5 |
Інтегральна формула Коші....................................................... |
18 |
1.6 |
Ряди Тейлора та Лорана ........................................................... |
21 |
1.7 |
Нулі аналітичної функції.......................................................... |
28 |
1.8 |
Ізольовані особливі точки........................................................ |
29 |
1.9 |
Лишки......................................................................................... |
30 |
2 ОПЕРАЦІЙНЕ ЧИСЛЕННЯ.......................................................... |
34 |
|
2.1Визначення перетворення Лапласа. Оригінал та
|
зображення функції................................................................... |
34 |
2.2 |
Властивості перетворення Лапласа......................................... |
35 |
2.3 |
Знаходження оригінала по зображенню................................. |
40 |
2.4Розв’язання задачі Коші для звичайних лінійних
|
диференціальних рівнянь з постійними коефіцієнтами |
........43 |
3 ІНДИВІДУАЛЬНІ ЗАВДАННЯ..................................................... |
46 |
|
3.1 |
Завдання 1 .................................................................................. |
46 |
3.2 |
Завдання 2 .................................................................................. |
47 |
3.3 |
Завдання 3 .................................................................................. |
48 |
3.4 |
Завдання 4 .................................................................................. |
50 |
3.5 |
Завдання 5 .................................................................................. |
51 |
3.6 |
Завдання 6 .................................................................................. |
54 |
3.7 |
Завдання 7 .................................................................................. |
55 |
3.8 |
Завдання 8 .................................................................................. |
56 |
3.9 |
Завдання 9 .................................................................................. |
60 |
3.10 |
Завдання 10 ................................................................................ |
64 |
3.11 |
Завдання 11 ................................................................................ |
65 |
Література.................................................................................................. |
67 |
|
Додаток. Таблиця зображень основних елементарних функцій........ |
688 |
|
4
ВСТУП
Методичні вказівки складені у відповідності до програми з курсу теорії комплексної змінної та операційного числення багатоступеневої підготовки фахівців і призначені для студентів заочної форми навчання, та для самостійної роботи денної форми навчання, що навчаються на факультетах радіоприладобудівному та інформатики і обчислювальної техніки.
У перших двох параграфах наведено стисло викладений теоретичний матеріал, проілюстрований багатьма прикладами, рисунками, зразками типових вправ.
Вказівки містять одну контрольну роботу з курсу теорії комплексної змінної та операційного числення. Індивідуальні завдання містять 30 варіантів. Номер варіанту визначається за останніми двома цифрами номера залікової книжки студента. Для визначення студентом номер варіанту, який він повинен виконати, слід знайти лишок від ділення числа, яке складається з двох останніх цифр його залікової книжки, на 30. Якщо немає лишку, виконується варіант №30.
Наприклад.
Номер залікової книжки – 926708 Після ділення 8 на 30 отримаємо лишок 8, тобто слід виконувати
варіант №8.
Номер залікової книжки – 926741 Після ділення 41 на 30 отримаємо лишок 11, тобто слід
виконувати варіант №11.

5
1 ТЕОРІЯ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ
1.1 Комплексні числа та дії над ними
Комплексним числом z в алгебраїчній формі називається вираз
z=х+iу, де х та у – дійсні, а i – уявна одиниця, i2 = −1. |
z |
= x −iy |
– |
спряжене комплексне число. |
y = Im z |
|
|
x = Re z – дійсна частина комплексного числа, |
– |
||
його уявна частина.
Комплексне число z=х+iу можна зобразити точкою площини хОу з координатами (х,у), також числу z можна поставити у
відповідність вектор r , який має напрямок з початку координат О в точку z (рис. 1.1).
Рисунок 1.1 |
|
Довжина вектора r має назву модуля комплексного числа: |
|
ρ = z = x2 + y2 |
(1.1) |
Кут ϕ , утворений з віссю Ох має назву аргумента ϕ = Argz , значення якого неоднозначне, всі його значення відрізняються на доданки, кратні 2π .
Якщо z=0, то Argz невизначено.
Головне значення аргумента позначається arg z і визначається
однозначно −π < arg z ≤ π . |
|
|
ϕ = Argz = arg z + 2kπ |
( k = 0; ±1; ± 2;....) |
(1.2) |

6
|
|
|
|
|
y |
, якщох > 0 |
|
|||
|
|
|
arctg |
|
|
|||||
|
|
|
x |
|
||||||
|
|
|
|
|
|
y |
|
|
(1.3) |
|
|
|
|
|
|
|
|
|
|
||
|
|
arg z = |
π + arctg |
|
, якщох< 0, y ≥ 0 |
|
||||
|
|
x |
|
|||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− π |
+ arctg |
|
, якщох< 0, y < 0 |
|
|||
|
|
|
x |
|
||||||
arg z = π |
|
|
|
|
|
|
|
|
|
|
, якщо x=0, y>0. |
|
|
|
|
|
|
|
|||
2 |
π |
|
|
|
|
|
|
|
|
|
arg z = − |
, якщо x=0, y<0. |
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
x = ρ cosϕ; x = ρ sin ϕ , тобто |
||
З рисунку |
1.1 видно, |
що |
|
|||||||
комплексне число можна записати у так званій тригонометричній формі:
z = x + iy = ρ(cosϕ +i sin ϕ) |
(1.4) |
Показникова форма комплексного числа: |
|
z = ρeiϕ |
(1.5) |
Дії над комплексними числами:
Нехай z1 = x1 +iy1 , z2 = x2 +iy2
z1 = z2 x1 = x2 , y1 = y2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
z1 ± z2 = (x1 ± x2 ) +i( y1 ± y2 ) |
|
|
|
|
|
|
|
|
||||||||||||||
z1 z2 = (x1x2 − y1 y2 ) +i(x1 y2 + x2 y1) = |
|
|
|
|
|
|
||||||||||||||||
= ρ ρ |
2 |
(cos(ϕ +ϕ |
2 |
)+i sin(ϕ +ϕ |
2 |
)) = ρ ρ |
|
ei(ϕ1 +ϕ2 ) |
|
|||||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
1 |
2 |
|
|
|
|||||
z1 |
= |
z1 |
|
|
= |
ρ1 |
|
|
|
|
|
|
)) = |
ρ1 |
|
|||||||
z2 |
(cos(ϕ |
−ϕ |
2 |
)+i sin(ϕ |
−ϕ |
2 |
ei(ϕ1 −ϕ2 ) |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
z2 |
|
z2 z2 |
|
ρ2 |
|
|
1 |
|
|
|
1 |
|
|
|
ρ2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(1.6)
(1.7)
(1.8)
(1.9)
Приклад 1.1
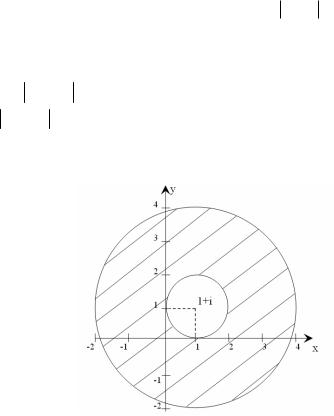
Визначити множину точок, які задовольняють наступним умовам: а) 1 ≤ z −1−i ≤ 3
б) − π4 < arg(z −1−2i) ≤ π6
7
Розв’язок
а) З геометричної точки зору рівняння z − z0 = r є рівнянням кола з центром в точці z0 і радіусом r .
Шукана множина точок повинна одночасно задовольняти двом умовам:
1. 1 ≤ z −1−i – зовнішність одиничного кола з центром в точці 1+і. 2. z −1−i ≤ 3 – внутрішність кола з радіусом 3 і центром в точці 1+і.
Тому шукана множина – це кільце, що обмежено концентричними колами радіусів 1 та 3 з центром в точці 1+і, включаючи самі кола (рис. 1.2).
Рисунок 1.2
б) комплексне число z-1-2i=z-(1+2i) зображується вектором, початок якого є точка 1+2i, а кінець – точка z.
Кут між цим вектором та віссю Ох ϕ = arg(z −1−2i) та він змінюються у межах від − π4 до π6 .
Тобто шукана множина точок – це частина площини між променями, що виходять з точки (1+2i), та які утворюють з віссю Ох
кути − π4 та π6 , включаючи верхній промінь (рис. 1.3).

8
Рисунок 1.3
Приклад 1.2
Зобразити лінію, для якої Re z2 = a2
Розв’язок
а) Знайдемо z2 : z2 = (x +iy)2 = x2 − y2 +i2xy , тоді Re z2 = x2 − y2 , тобто рівняння Re z2 = a2 можна записати так:
x2 − y2 = a2
Це, як відомо, рівнобічна гіпербола.
Для піднесення в степінь використовують формулу Муавра:
zn = ρn (cos nϕ +i sin nϕ) |
(1.10) |
Приклад 1.3
Обчислити (−  3 −i)5
3 −i)5
Розв’язок
а) Знайдемо тригонометричну форму числа (−  3 −i). Для цього знайдемо його модуль за формулою (1.1):
3 −i). Для цього знайдемо його модуль за формулою (1.1):
ρ =  3 +1 = 2
3 +1 = 2
Та аргумент за формулою (1.2):

9
|
ϕ = arg z = −π + arctg |
|
−1 |
= −π + π |
= − |
5π |
||||||||||||
Тоді за формулою (1.4): |
|
|
− 3 |
|
|
|
6 |
|
|
6 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
− |
|
|
|
|
|
− |
5π |
|
|
|
|
5π |
|
||||
|
3 − i = 2 cos |
|
|
+ i sin − |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Використовуючи формулу (1.10), одержуємо: |
|
|
||||||||||||||||
|
5 |
|
5 |
|
|
25π |
|
|
|
|
− |
25π |
|
|
= |
|
||
(− 3 − i) |
= 2 |
cos − |
|
|
|
+ i sin |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
π |
|
|
π |
|
|
|
3 |
|
1 |
|
|
|
|||
− |
− |
|
|
− i |
|
= 16 3 −16i |
||||||||||||
= 32 cos |
+ i sin |
|
|
= 32 |
|
|
|
|
||||||||||
|
|
|
6 |
|
|
6 |
|
|
|
2 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Корені степеня n визначаються за формулою:
n |
|
ϕ + 2kπ |
|
z = n ρ cos |
n |
|
|
Приклад 1.4
Знайти а) 3 1+ i ;
Розв’язок
а) Для числа 1+і
| z |=  1+1 =
1+1 =  2;
2;
1+ i = |
|
π |
+ |
2 cos |
4 |
||
|
|
|
+ isin |
ϕ + 2kπ |
k = 0,1,2....n −1 (1.11) |
|
n |
, |
||
|
|
|
|
б) 3 1
ϕ = arg z = arctg 11 = π4
i sin π
4
Використовуючи формулу (1.11): |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
π |
+ 2πk |
|
π |
|
|
|
|
|
|
3 |
|
1 |
|
4 |
|
4 |
+ 2πk |
|
||
3 |
1 |
+ i = |
2 |
2 |
|
|
+ i sin |
|
|
k = 0,1, 2 |
|||
|
|
|
|||||||||||
|
|
|
cos |
|
3 |
|
3 |
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ми одержимо три різних значення кореня:

|
|
|
|
|
|
|
|
|
|
|
10 |
|
z1 = |
6 |
|
π |
+i sin |
π |
|
|
(k = 0) |
||||
|
2 cos |
12 |
12 |
, |
|
|||||||
|
|
|
|
|
|
|
|
|
||||
z2 = |
6 |
|
9π |
|
+i sin |
9π |
|
|
(k =1) |
|||
|
2 cos |
12 |
|
12 |
, |
|
||||||
|
|
|
|
|
|
|
|
|
||||
z3 = |
6 |
|
17π |
+i sin |
17π |
|
(k = 2) |
|||||
|
2 cos |
12 |
|
12 |
, |
|||||||
|
|
|
|
|
|
|
|
|
||||
б) для числа z=1: ρ =1; ϕ = 0 , за формулою (1.11):
3 1 = cos |
2πk +i sin 2πk , |
|
|
k = 0,1, 2 |
|
|||
|
|
3 |
|
3 |
|
|
|
|
z1 = cos 0 +i sin 0 =1, |
|
(k = 0) |
|
|||||
z2 |
= cos |
2π |
+i sin 2π |
= − |
1 |
+ |
3 i, |
(k =1) |
|
|
3 |
3 |
|
2 |
|
2 |
|
z |
= cos 4π |
+i sin 4π |
= − 1 |
− |
3 і, |
(k = 2) |
||
3 |
|
3 |
3 |
|
2 |
|
2 |
|
|
|
|
|
|
||||
1.2 Основні елементарні функції комплексної змінної
Показникова функція ez обчислюється за допомогою формули Ейлера:
ez = ex+iy = ex (cos y +i sin y)
Тригонометричні функції sinz i cosz можна обчислити за формулами
sin z = |
eiz −e−iz |
, |
cos z = |
eiz + e−iz |
||||
|
2i |
2 |
|
|||||
|
|
|
|
|
||||
Функції tgz i ctgz визначаються рівностями |
|
|
|
|||||
tg z = |
sin z |
, |
|
ctg z |
= |
cos z |
|
|
|
|
sin z |
||||||
|
|
cos z |
|
|
|
|||
