Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Запорожский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

математика 1874

.pdf

Скачиваний:

Добавлен:

07.02.2016

Размер:

530.12 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

6. (1 + x)α = 1 + α x +

α (α − 1)

+ ... +

α (α − 1)...(α − (n − 1))

xn + ...

(− 1< x < 1)

= 1 + x + x2

+ ... + xn + ...

(− 1< x < 1)

− x

f (x)= x2 ln(1 + x2 )

Приклад 18. Розкласти в ряд Тейлора функцію

за степенями х.

Розв′язання.

Так як

ln(1 + x)= x −

− ... + (− 1)n−1

+ ...

(− 1< x < 1)

то замінючи в останній рівності х на х2, маємо:

ln(1 + x2 )= x2 −

− ... + (− 1)n−1

x2n

+ ... (

< 1)

і тому

x2 ln(1 + x2 )= x4

−

− ... + (− 1)n

x2n+ 2

+ ...

(

< 1)

f (x)=

Приклад 19. Розкласти в ряд Тейлора функцію

за

x + 3

степенями х. Розв′язання.

Перетворимо цю функцію так, щоб можна було використати

розклад функції	1		1	=	m
		. Нехай				, тоді
	1 − x		x + 3		1 − n(x − 1)

1 − n(x − 1)= m(x + 3). Визначимо звідси m i n.

При х=1 маємо 1 = 4m i m = 1 , при x = −3 маємо 1 + 4n = 0 і n = − 1 .

					4			4
Отже,	1	=		1	1
Отже,	x + 3	=					x − 1
		4			1 −		x − 1
					1 −		− 4
							− 4
Замінюючи в розкладі функції
			1			= 1 + x + x2 + ... + xn + ...		(− 1< x < 1)
		1 − x				= 1 + x + x2 + ... + xn + ...		(− 1< x < 1)
		1 − x

хчерез x − 1 , одержимо

−4

1			1			x − 1		(x − 1)2		− ... + (− 1)	n (x − 1)n
		=		1	−		+						+ ...
		=		1	−		+		2			n	+ ...
	x + 3		4			4		4	2		4	n
	x + 3		4			4		4			4
Цей розклад має місце, якщо

x − 1 < 1, x − 1 < 4 , звідси − 4 < x − 1 < 4, отже, − 3 < x < 5 .

− 4

Наближені обчислення за допомогою рядів

Для обчислення наближеного значення функції f (x)в її розкладі

в степеневий ряд зберігаються перші п членів, а останні члени відкидаються. Для оцінки похибки знайденого наближеного значення потрібно оцінити суму відкинутих членів. Якщо ряд знакосталий, то ряд складений з відкинутих членів, порівнюють з нескінченно спадною геометричною прогресією. Якщо ряд знакозмінний, члени якого задовольняють умови теореми Лейбніця, то використовують

оцінку

Rn (x)

un+1

, де un+1

- перший з відкинутих членів ряду.

Приклад 20. Обчислити 1,004 з точністю до 0,00001.

Розв′язання.

Використаємо формулу :

(1 + x)m = 1 +

x +

m(m − 1)

x2 + ... +

m(m − 1)...(m − n + 1)

xn + ...

Тут m =

, x = 0,004 . Тоді

− 1

(0,004)2

1,004 = 1 + 0,004 + 2

(0,004)2 + ... = 1 + 0,002 −

+ ...

2! 4

Зауважимо, що знаки одержаного ряду, починаючи із другого, чергуються. Обмежившись сумою перших двох членів, одержимо

1,004 = 1,002

Оцінюючи абсолютну похибку, маємо

∆ < (0,004)2 =

0,000002 .

2! 4

Отже, значення корня знайдено з вказаною точністю.

Приклад 21. Обчислити наближено 3

9 з точністю до 10-3.

Розв′язання.

Число 9 запишемо так:

9 = 23 +

1 =

1 1/ 3

23 1 +

3 1 +

; 3

= 2 1 +

Використовуючи формулу

(1 + x)m = 1 +

x +

m(m − 1)

+ ... +

m(m − 1)...(m − n + 1)

xn + ...,

де x =

, m =

, одержуємо

знакопочережний

ряд, що

задовольняє

умови теореми Лейбніця:

1 2 5

9 =

−

2 1 +

= 2 1

2! 32

... =

3 8 32

33 3! 83

= 2 +

−

+ ...

288

Так

як

четвертий

член

ряду

1 2 5

< 10−3 ,

похибка не

33 2! 83

перевищує модуля першого з відкинутих членів, то обмежуємось першими трьома членами ряду. Отже,

3 9 = 2 + 0,0833 − 0,0035 = 2,0798 2,080

Приклад 22. Обчислити наближено ∫4e− x2 dx , взявши два члени

розкладу в ряд підінтегральної функції, оцінити похибку. Розв′язання.

Розклавши підінтегральну функцію в ряд

e− x2 = 1 − x2 +	x4	− ...,

2!
одержуємо:

1/ 4			2	1/ 4				2			x	4								x	3		x		5		1/ 4
1/ 4			2	1/ 4								4									3				5		1/ 4
∫	e	− x		dx = ∫					+					−								+						=
∫	e			dx = ∫	1− x				+	2!				−	... dx =			x −		3		+	2	5		− ...		=
0				0						2!										3			2	5			0
0				0																							0
						=		1	−			1			+	1			− ....

								4			43 3						45 2 5
Третій член ряду a3						=		1					= 0,000098 < 10−4.

							5 2
						4	5 2			5

Якщо в знакопочережному ряді суму ряду замінити сумою двох доданків, то похибка менша, ніж третій член ряду, тобто менша, ніж 10-4, маємо:

1/ 4

∫ e− x

≈

−

= 0,25000 − 0,00521 = 0,24479 0,2448

Приклад 23. Знайти п′ять перших членів розкладу в степеневий

ряд розв′язку диференціального рівняння y′ = x2

+ y 2 , якщо у(0)=1.

Розв′язання.

З даного рівняння знаходимо, що y′(0)= 0 + 1 = 1 .

Диференціюємо дане рівняння:

y′′(0)= 2

y′′ = 2x + 2yy′,

y′′′ = 2 + 2y′2

+ 2yy′′′

y′′′(0)= 2 + 2 + 2 2 = 8

y IY = 4y′y′′ + 2y′y′′ + 2yy′′′

y IY (0)= 4 2 + 2 2 + 2 8 = 28

Отже, так як частинний розв′язок даного рівняння знаходимо у

вигляді степеневого ряду

y′′(0)

y(n) (0)

y(x)= y(0)+ y′(0)x +

... +

+ ....

то в нашому випадку маємо розв′язок

y = 1 + x +

x3 +

x4 + ... = 1 + x + x2

x3 +

x4 + ...

Приклад

24.

Знайти

розв′язок

диференціального

рівняння

y′′ − 2xy′ − y = 0 , що задовольняє умови y(0)= 0, y′(0)= 1.

Розв′язання.

Частинний розв′язок диференціального рівняння шукаємо у вигляді степеневого ряду

y(x) = y(0)+ y′(0)x + y′′(0) x2 + ... + y(n0 )(0) xn + ... .

2!	n!
З початкових умов випливає, що	y(0)= 0, y′(0)= 1. З даного

рівняння, підставляючи в нього x = 0, y′(0)= 1, знаходимо y′′(0)= 0 . Диференціюючи задане рівняння по х, одержимо:

y′′′ = 2y′ + 2xy′′ + y′ = 3y′ + 2xy′′

y′′′(0)= 3

y(4) = 3y′′ + 2y′′ + 2xy′′′ = 5y′′ + 2xy′′

y(4) (0)= 0

y(5) = 5y′′′ + 2y′′′ + 2xy(4) = 7 y′′′ + 2xy (4)

y(5) (0)= 3 7

y(6) = 7 y(4) + 2y(4) + 2xy(5) = 9y(4) + 2xy(5)

y(6) (0)= 0

y(7) = 9y(5) + 2y(5) + 2xy(6) = 11y(5) + 2xy(6)

(7)

( )

= 3

Таким чином, частинний розв′язок рівняння буде

y(x)= x +

x3 +

3 7

3 7 11

x7 + ... +

3 7 ...(4n − 1)

x2n+1 + ....

(2n + 1)!

4. РЯДИ ФУР′Є

Розклад в ряд Фур′є функції з періодом 2π

Рядом Фур′є функції f (x), яка є періодичною з періодом 2π, називається тригонометричний ряд

	∞
a0 + ∑(an cos nx + bn sin nx),
2	n=1

коефіцієнти якого визначаються за наступними формулами:

f (x)dx,

f (x)cos nxdx,

f (x)sin nxdx ,

∫

−π

n = 1, 2,3...

Коефіцієнти a0 , an , bn , знайдені за цими формулами, називаються

коефіцієнтами Фур′є.

Таким чином, якщо задана періодична функція з періодом 2π, то можна для даної функції скласти ряд Фур′є.

Достатні умови розкладу функції в ряд Фур′є визначаються теоремою Діріхле.

Теорема. Якщо періодична функція з періодом 2π на відрізку [-π;π] неперервна або має скінчене число розривів першого роду, і якщо відрізок [-π;π] можна розбити на скінчене число відрізків так, що всередині кожного з них f (x) монотонна, то ряд Фур′є, складений для

функції f (x), збігається для всіх значень х. При цьому сума одержаного ряду дорівнює значенню функції в точках неперервності функції. В точках розриву функції f (x) сума ряду дорівнює середньому арифметичному границь зліва і справа.

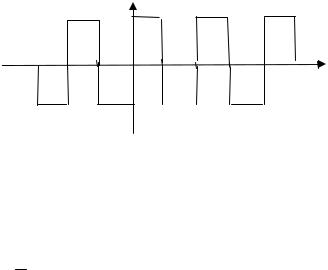
Приклад 25. Розкласти в ряд Фур′є функцію з періодом 2π, задану на інтервалі − π < x ≤ π так:

( ) − 3 , - π < x ≤ 0 f x = 5, 0 < x ≤ π

Розв′язання.

Графік даної функції має вигляд:

-3

-2π -π 0

2π 3π

4π

5π х

-3

Задана функція

f (x)

задовольняє умовам теореми про розклад в

ряд Фур′є. Обчислюємо коефіцієнти Фур′є функції

f (x):

(− 3x

∫ f (x)dx =

∫

(− 3)dx + ∫5dx

−π + 5x

−π

= π1 (− 3π + 5π )= 2;

f (x)cos nxdx =

(− 3)cos nxdx +

∫

5cos nxdx =

−π

π −π

−

sin nx

= 0;

−π

f (x)sin nxdx =

(− 3)sin nxdx +

∫

5sin xnxdx =

−π

π −π

(3 − 3cosπn − 5cosπn + 5)=

cos nx

−

cos nx

πn

−π

(1− cosπn) =

(1− (− 1)n )=

приn непарному,

πn

приn парному.

Підставивши знайдені коефіцієнти, одержимо розклад в ряд Фур′є

заданої функції:

1 +

sin x

sin 3x +

sin 5x +

sin 7x + ... .

Сума цього ряду дорівнює функції в будь-якій точці

неперервності цієї функції.

В точках розриву x = ±nπ (n = 0,1, 2,3...)

сума

ряду

дорівнює

− 3 + 5 = 1,

тобто

дорівнює середньому

арифметичному значень даної функції зліва і справа від точки розриву.

Ряди Фур′є для парних і непарних функцій з періодом 2π.

Якщо функція f (x)парна, тобто f (− x)= f (x), то при її розкладі

в ряд Фур′є маємо
a =	2	π	f (x)dx, a		=	2	π	f (x)cos nxdx, b = 0 (n = 1, 2,3...)
	π	∫				π	∫
0				n				n

		0					0

і ряд має вигляд:

Для непарної функції, маємо:

a = 0; an = 0; bn =

	∞
+ ∑an cos nx
	n=1	умові f (− x)= − f (x)
що задовольняє		умові f (− x)= − f (x)
2	π
2	∫ f (x)sin nx dx,	(n = 1, 2,3...)
π	∫ f (x)sin nx dx,	(n = 1, 2,3...)
π	0
	0

і ряд має вигляд:

∞

∑bn sin nx

n=1

Приклад 26. Розкласти в ряд Фур′є функцію f (x)= x з періодом

2π, задану на інтервалі − π < x < π . Розв′язання.

Графік даної функції має вигляд y

		π
-2π	-π	π	2π	3π	x

Ця функція задовольняє умовам теореми про розклад в ряд Фур′є. Вона парна. Отже, bn = 0 .

Визначаємо a0 i an :

∫

xdx =

= π

u = x,

dv = cos nxdx

x cos nxdx

∫0

= dx,

v =

sin nx

2 x

= sin nx

π n

	1	π		2

−		∫sin nxdx	=			cos nx
					2
	n	0		πn

= 2 (cosπn − cos 0)=

0 πn2

								79
			(		)		0, приn непарному
	2			n			4
=						=	4
=			(− 1)		− 1	=			, приn непарному
	πn	2				-
	πn	2				-	πn	2
							πn

Ряд Фур′є має вигляд:

cos x

cos 3x

cos 5x

cos 7x

−

+ ... .

Задана функція неперервна на всій числовій вісі, отже, її сума дорівнює f (x).

Розклад в ряд Фур′є функцій з періодом 2l.

Нехай функція, що задовольняє умовам Діріхле, має період 2l. Рядом Фур′є для такої функції називається ряд

∞

nπx

+ ∑ an cos

+ bn

sin

n=1

коефіцієнти якого визначаються за формулами:

a0 =

l f (x)dx, an

f (x)cos

nπx

dx,

f (x)sin

nπx

∫

l ∫

−l

(n = 1,2,3...) .

f (x) парна, то

Якщо функція

a0 =

l f (x)dx, an

f (x)cos

nπx

dx, bn

= 0

(n = 1,2,3...) ,

∫

а якщо непарна,то

= 0, a

= 0

l f (x)sin

nπx

dx , ( n = 1,2,3...)

l ∫

f (x) з періодом 6,

Приклад 27. Розкласти в ряд Фур′є функцію

задану на інтервалі − 3 < x ≤ 3 формулою

f (x) = −2x + 3 .

Розв′язання.

Графік даної функції має вигляд:

-3

-9

-3

Обчислимо коефіцієнти Фур′є для даної функції:

a0 =

(− 2x + 3x)dx =

(− x2 + 3x)3

(− 9 + 9 + 9 + 9) = 6.

3 −∫3

−3

u = −2x + 3, dv = cos

nπx

an =

(− 2x + 3)cos πnx dx =

3 −∫3

du = −2dx, v =

sin

nπx

nπ

(− 2x + 3)

sin πnx

nπx

∫ sin

nπ

πn

−3

nπx

(cos nπ − cos(− nπ )) = 0 .

0 −

cos

= −

n2π 2

−3

n2π

= −2x + 3, dv = sin

nπx

3 (− 2x + 3)sin

nπx

dx =

bn =

dx =

3 −∫3

du = −2dx, v = −

cos

nπx

nπ

(− 2x + 3)

− 3 cos

nπx

−

∫cos

dx =

nπ

−3

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.02.2016171.52 Кб7Маршрутная карта.doc
#
18.07.2019125.44 Кб4Массовые репрессии и политические процессы 20-х....doc
#
07.02.2016588.27 Кб13матанчик 4 идз.pdf
#
07.02.20161.16 Mб9математика 1227.pdf
#
07.02.2016459.93 Кб7математика 1229.pdf
#
07.02.2016530.12 Кб7математика 1874.pdf
#
07.02.2016476.22 Кб8МАТЕМАТИКА 2Ч.pdf
#
07.02.2016309.25 Кб16математика 3700.pdf
#
07.02.2016594.89 Кб716математика 3701.pdf
#
07.02.20163.15 Mб15Математика задания(30 вариантов).doc
#
07.02.20165.01 Mб110Матеріалознавство.pdf