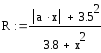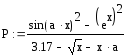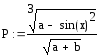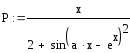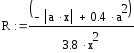1.1.10 Аналітичні обчислення
Пакет MathCadмістить велику кількість команд аналітичних обчислень. Найбільш прості: Expand - розкриття дужок, Collect -приведення членів, Factor - розкладання на множники,Simplify– спрощення виразів.
Приклад
Використання символьного знака рівності
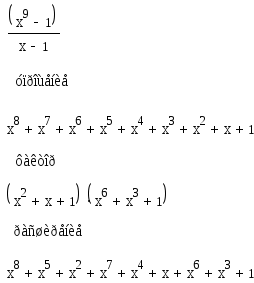
Expand- розкриття дужок
Для поліноміальних виразів розкриває дужки, а дрібно-раціональні вирази приводить до виду, придатному для інтегрування. При цьому команду Expandтреба використовувати з панеліSymbolic.
Приклад
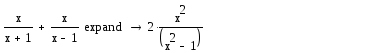
Collect-приведення членів
Команда Collect використовується для приведення подібних членів (групування по ступенях) у виразі А за змінною VAR.
Приклад
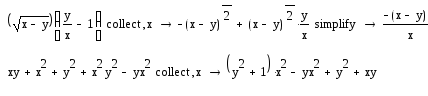
Simplify – спрощення виразів
Режим автоматичного спрощення полягає у використанні інформації про властивості математичних функцій для перетворення виразів до більш компактної форми. При цьому команду Simplify треба використовувати з панелі Symbolic.
Приклад
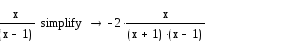
1.2Лабораторне завдання
Кожне завдання виконувати у окремому документі, результати виконання зберегти у новому файлі за ім’ям zav_(номер завдання), на приклад: zav_1.
1.2.1 Обчислення функцій
Згідно варіанту визначити функції Р(a,b,x) та R(a,b,x) та обчислити їх для значення аргументуx, якій вибрати самостійно з урахуванням області існування функції. Обчислення виконати двома способами.
Варіанти завдань
|
|
|
a=2.95; b=1; |
|
|
|
a=3; b=0.3; |
|
|
|
а = 0.52; b = 2; |
|
|
|
а = 7; |
|
|
|
a=7.4; |
|
|
|
а = 1.2; b = –0.7; |
|
|
|
а=3.18; b=2; |
|
|
|
а=8; |
|
|
|
а = 3.5; b = –0.4; |
|
|
|
а = 0.5; b = –1.9; |
|
|
|
а = 3.8; b = 1.1; |
|
|
|
а = 3.8; b =1.1; |
|
|
|
a = 2.6; b = 3.4; |
|
|
|
a = 25; |
|
|
|
a = 1.4; b = 0.3; |
|
|
|
a = –0.8; |
|
|
|
a = 12.3; |
|
|
|
а = 4; |
|
|
|
a = –0.8; b = 1; |
|
|
|
b = 1; |
|
|
|
a= 1.8; b = 2; |
|
|
|
b = 1; |
|
|
|
a = 1.5; b = 7; |
|
|
|
a= 2.0; |
|
|
|
|
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
1.2.2 Використання дискретної змінної
За умовами завдання 2.1 вивести таблицю значень функцій Р(a,b, х) та R(a,b, x) у заданому інтервалі аргументуxзгідно варіанта. Забезпечити виведення не менше 10 значень аргументуxта функцій.
|
х |
Р(х) |
x |
R(х) |
| |
|
|
|
|
|
| |
|
1 |
у інтервалі 0 хз кроком/20; | ||||
|
2 |
у інтервалі 0<x<2з кроком/(1+b); | ||||
|
3 |
у інтервалі 0< х<2з кроком/10; | ||||
|
4 |
у інтервалі 0< х<2з кроком/10; | ||||
|
5 |
10значень функції у інтервалі 0< х<; | ||||
|
6 |
10 значень функції у інтервалі 0< х<; | ||||
|
7 |
10 значень функції у інтервалі 0< х</25; | ||||
|
8 |
у інтервалі 0< х<2з кроком/8; | ||||
|
9 |
у інтервалі 0< х<2з кроком/6; | ||||
|
10 |
25 значень функції у інтервалі 0< х <2; | ||||
|
11 |
25 значень функції у інтервалі 0< х <2; | ||||
|
12 |
25 значень функції у інтервалі 0< х <3; | ||||
|
13 |
30 значень функції у інтервалі 0< х <15; | ||||
|
14 |
у інтервалі 0< х <1.5з кроком/15; | ||||
|
15 |
у інтервалі 0< х <3з кроком/15; | ||||
|
16 |
у інтервалі 0< х <з кроком/20; | ||||
|
17 |
у інтервалі 0< х <з кроком/20; | ||||
|
18 |
10 значень функції у інтервалі 0<х<; | ||||
|
19 |
15 значень функції у інтервалі 0< х <2; | ||||
|
20 |
у інтервалі 0< х <3з кроком/4; | ||||
|
21 |
у інтервалі 0< х <з кроком/30; | ||||
|
22 |
у інтервалі 0< х <2з кроком/10; | ||||
|
23 |
20 значень функції у інтервалі 0< х <2; | ||||
|
24 |
15 значень функції у інтервалі 0< х <3; | ||||
|
25 |
у інтервалі 0< х <з кроком/15; | ||||
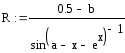
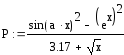
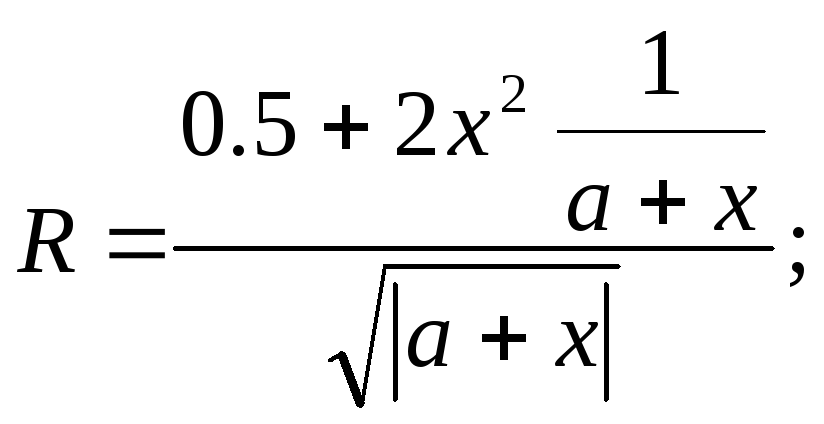
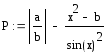
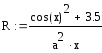
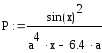