8.8. Минимизация переключательных функций методом неопределенных коэффициентов

Можно показать, что любая переключательная функция представима в так называемой универсальной нормальной форме (УНФ), например, для n=2:

Такое выражение – дизъюнкция всевозможных импликант каждой конституенты. В УНФ каждый из неопределенных коэффициентов описывает вхождение () или невхождение () соответствующей импликанты в выражение функции. Путем определения этих коэффициентов и производится минимизация. Представим УНФ в несколько иной форме:

Если функция равна нулю на некотором наборе переменных, то, очевидно, что все соответствующие этому набору коэффициенты также будут равны нулю. На этом и строится процедура минимизации. Вычеркиваются (удаляются) члены УНФ, соответствующие нулевым наборам из всех наборов, после чего получают простые импликанты. Далее, путем определения оптимального покрытия всех конституент, определяют минимальную форму представления функции.

Минимизируем, например, функцию «импликация» которая равна нулю на единственном наборе 10. Тогда получим:

Видим, что импликанта покрывает наборы 00(0) и 01(1), импликанта x₂ – наборы 11(3) и 01(1). Поэтому

Что и требовалось показать.

9. Понятие об автомате и его математическом описании

9.1. Основные определения теории конечных автоматов

Конечным автоматом (просто автоматом) называется система (пятерка) [19]:

S=<X,Y,Z,,>,

в которой Х={х₁,х₂,...,х_i} – конечное входное множество (входной алфавит); Y={y₁,y₂,...,y_j} – конечное множество внутренних состояний автомата (алфавит состояний); Z={z₁,z₂,...,z_k} – конечное выходное множество (выходной алфавит);  – функция переходов (из состояния в другие состояния);  – функция выходов.

Если указанные множества бесконечные, то это уже не конечный автомат, но может быть дискретный автомат.

Если функция переходов – вероятностная, то это недетерминированный автомат.

Если в автомате выделено одно состояние, называемое начальным (обычно это y₁), то полученный автомат называется инициальным и обозначается <S,y>. Таким образом, по неинициальному автомату с i состояниями можно i различными способами определить инициальный автомат.

Функция переходов представляет собой отображение вида : или в другом виде:

y(t+1)=[x(t),y(t)],

где x(t),y(t),y(t+1) – конкретные символы алфавитов Х и Y соответственно в моменты автоматного времени t, t+1 (в тактах t и t+1); y(t) называется текущим внутренним состоянием при соответствующем х(t), а y(t+1) – последующим внутренним состоянием.

Иначе говоря, функция переходов определяет последующее состояние автомата по заданному текущему и входному символу.

Функция выходов представляет собой отображение вида : ХYZ или в другом виде:

z(t)=[x(t),y(t)],

где x(t),y(t),z(t) – конкретные символы алфавитов X,Y,Z соответственно. Мы не будем особо выделять последующие значения x(t+1) и z(t+1), поэтому зависимость от t будем указывать только для внутреннего состояния, чтобы отделять y(t) от y(t+1).

Указанная функция выходов – функция так называемого автомата Мили.

В теории конечных автоматов рассматривается также автомат Мура, у которого функция выходов проще: : илиz(t)=[y(t)].

Автомат называется комбинационным, если для любого входного символа х и любых состояний y_i, y_j (х,y_i)=(х,y_j)=z, иначе говоря, если выходной символ z не зависит от состояния и определяется текущим входным символом. Говорят, что у такого частного класса автомата все состояния эквивалентны и, следовательно, комбинационный автомат имеет одно состояние. Такой автомат задается тройкой:

S=<X,Z,>.

Рассмотрим представление конечного автомата в виде «черного» ящика (рис. 51).

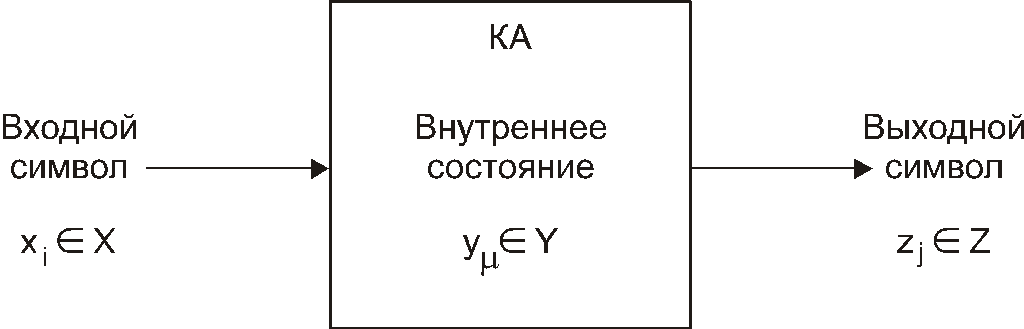
Рис. 51. Конечный автомат (КА) в виде «черного» ящика

В комбинационном автомате внутренних состояний не указывают.

Входное слово – последовательность входных символов.

Выходное слово – последовательность выходных символов, соответствующих входному слову. В конечном автомате также выделяется последовательность символов внутренних состояний, соответствующих входному слову.

Большой вклад в теорию дискретных (цифровых) автоматов внесли отечественные ученые: М.А. Гаврилов, который опубликовал первую в мире монографию «Теория релейно-контактных схем» (1950 г.), В.М. Глушков, В.Н. Рогинский, П.П. Пархоменко, В.Г. Лазарев, С.И. Баранов, А.Д. Закревский, Э.А. Якубайтис, С.В. Яблонский, В.И. Варшавский и др.