3.8. Решение комбинаторных уравнений

В комбинаторике тоже могут решаться уравнения, особенностью которых является то, что неизвестная принадлежит множеству натуральных чисел. Например, уравнения вида ,xN, где N – множество натуральных чисел или вида:

, xN (решите!).

При решении комбинаторных уравнений часто необходимо уметь выполнять действия с факториалами типа:

,

или:

.

Например, в задаче о сравнении пар записей в базе данных из n записей:

, – что и требовалось доказать.

В комбинаторике рассматриваются и другие типовые комбинаторные комбинации, например, разбиения n-элементного множества на k подмножеств, которые называются блоками разбиения. В информатике вычисления на конечных математических структурах часто называют комбинаторными вычислениями, и они требуют комбинаторного анализа для установления свойств и оценки применимости используемых алгоритмов. На рис. 11 приведен один из возможных вариантов классификации основных комбинаций.

Рис. 11. Основные комбинации

Комбинаторные задачи могут быть решены, например, системой компьютерной математики Matematica (3,4) фирмы Wolfram Research,Inc. – пакет расширения «Дискретная математика» (DiscreteMath) – комбинаторика и ее функции (Combinatorica, CombinatorialFunctions): функции перестановок и сочетаний и др.

4. Основные понятия теории графов

4.1. Способы задания графов

Совокупность множества М с заданным на нем бинарным отношением ТМ² [9] называется графом

G=<M,T>,

где М – носитель графа – множество вершин, изображаемых точками, Т – сигнатура графа – множество линий, обозначающих отношения и называемых ребрами.

Между элементами М и Т определено отношение инцидентности, т.е. связи между двумя элементами множества М через один элемент множества Т. Примеры графов: отношения отцовства и материнства на множестве людей, отношения подчиненности, карты дорог местности, электрические схемы соединений приборов и т.д.

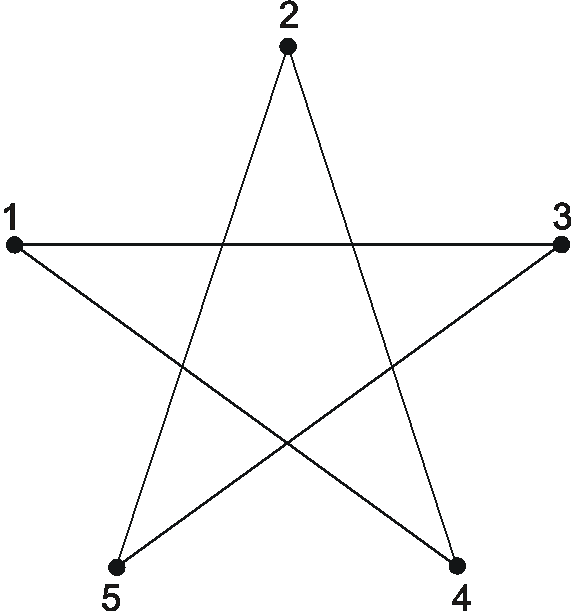
Рис. 12. Пример графа «звезда»

М={1,2,3,4,5},

Т={(1,3),(1,4),(2,4),(2,5),(3,1),(3,5),(4,2),(4,1),(5,3),(5,2}).

Множество линий-ребер в Т задается обозначением пары (i,j), где i,j – инцидентные вершины, отношение Т – «быть связанным».

Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий. В этих задачах несущественно, соединены ли точки конфигурации отрезками прямых или они криволинейны, какова длина линий и другие геометрические характеристики конфигурации. Важно лишь, что каждая линия соединяет какие-либо две из заданных точек [24].

Первые серьезные результаты теории графов связаны с решением задач построения электрических цепей (Г. Кирхгоф) и подсчета числа химических соединений с различными типами молекулярных связей (А. Кэли). Изобразите в виде графа молекулу

В 30-е годы ХХ века благодаря трудам Д. Кенига [19] теория графов стала развиваться как самостоятельный раздел математики.

Широкое развитие теория графов получила с 50-х годов ХХ века в связи с появлением такой науки, как кибернетика. Графы применяют при анализе функционирования систем. С отдельными компонентами изучаемой системы удобно связывать вершины графа, а с парами взаимодействующих компонент – его ребра. Такой граф называют структурным графом системы.

В некоторых задачах существенно направление ребер графа. Направленные ребра называют дугами, а содержащий их граф – ориентированным (орграфом). Таковым графом может быть изображена диаграмма Хассе. Соответственно граф с неориентированными ребрами называется неориентированным.

Множество ребер может быть пусто. Если же множество вершин пусто, то пусто и множество ребер. Такой граф называется пустым. Линии, изображающие ребра, могут пересекаться на изображении графа, но точки их пересечений не являются вершинами. Различные ребра могут быть инцидентны одной и той же паре вершин, в этом случае они называются кратными. Граф, содержащий кратные ребра, называют мультиграфом (псевдографом). Ребро (дуга) может соединять некоторую вершину саму с собой, такое ребро (дуга) называется петлей. Будем рассматривать конечные графы, содержащие конечные множества вершин и ребер (дуг).

Рассмотрим предложенную фон Нейманом архитектуру ЭВМ, которая состоит из множества устройств М={а,b,c,d,e}, где а – устройство ввода, b – арифметическое устройство (процессор), с – устройство управления, d – запоминающее устройство, е – устройство вывода [9-10].

Информационный обмен между этими устройствами задается графом (рис. 13).

Рис. 13. Граф, описывающий архитектуру

фон Неймановской ЭВМ

Вершины графа на рис. 13 для удобства изображены кружками, а не точками, как на рис. 11.

Граф можно задать так называемой матрицей смежности, каждой i-ой строке (j-му столбцу) которой однозначно сопоставляют элемент множества М, между которыми выполняется отношение смежности. Две вершины, инцидентные одному ребру, смежны. Два ребра, инцидентные одной вершине, тоже смежны. Тогда каждая клетка b_ij взаимно однозначно соответствует элементам множества ММ=М². Клетку b_ij, которая соответствует элементу, принадлежащему бинарному отношению ТМ², отмечают, например, единицей, а в остальные клетки записывают нули.

Рассмотрим матрицу смежности В для графа, изображенного на рис. 13. Устройства i,j находятся в отношении Т, если из устройства i информация поступает в устройство j.

Граф можно задать и с использованием перечисления его дуг, как это сделано на рис. 13:

М={а,b,с,d,е},

Т={(а,b),(а,с),(а,d),(b,с),(b,е),(b,d),(с,а),(с,b),(с,d),(с,е),(d,с),(d,b),(d,е),(е,с)}.

Граф можно задать в виде так называемого фактор-множества, представленного парами «элемент множества М – подмножество М, представляющее собой окрестность единичного радиуса этого элемента»:

[<a,{b,c,d}>,<b,{c,d,е}>,<c,{a,b,d,e}>,<d,{b,c,e}>,<e,{c}>].

Ориентированный граф может быть задан и матрицей инцидентности А размерностью nm: A=a_ij, где n=|M|, m=|Т|, у которой

если вершина a_i является концом дуги t_j;

если вершина a_i является началом дуги t_j;

если вершина a_i не инцидентна дуге t_j,

, .

Так, для ориентированного графа (рис. 14) матрица инцидентности имеет вид:

Рис. 14. Некоторый ориентированный граф

В описанном виде матрицы инцидентности применимы только к графам без петель, в случае наличия которых матрицу надо разбить на две полуматрицы: положительную и отрицательную. Ориентированный граф также может быть задан матрицей смежности.

Для графов с кратными ребрами в матрице смежности указывают кратность ребер, например, для графа, изображенного на рис. 15, матрица смежности представляется в виде:

Такой граф называют мультиграфом.

Рис. 15. Некоторый ориентированный мультиграф

Граф называется нагруженным, если каждому ребру (дуге) поставлено в соответствие некоторое действительное число (длина дуги, вес дуги, стоимость дуги и т.д.).

Представим в виде графа некоторые бинарные отношения [9]. Отношение Т в множестве М рефлексивно, как мы уже знаем, если для каждого элемента mМ справедливо (m,m)Т. На графе это изображается петлей (рис. 16а). На матрице смежности графа с рефлексивным отношением все элементы, лежащие на главной диагонали отмечены единицами.

Отношение во множестве М называется симметричным, если из (m_i,m_j)Т следует (m_i,m_j)М, m_im_j (рис. 16б). Матрица смежности симметричного отношения симметрична относительно главной диагонали.

Отношение Т в множестве М называется транзитивным, если из (m_i,m_j)Т, (m_i,m_k)Т следует (m_i,m_k)Т m_i, m_j,m_kМ, m_im_j, m_im_k, m_jm_k (рис. 16в).

В графе, задающем транзитивное отношение Т, для всякой пары дуг таких, что конец первой совпадает с началом второй, существует транзитивно замыкающая дуга, имеющая общее начало с первой и общий конец со второй.

Рис. 16. Изображения бинарных отношений в виде графа

а) рефлексивное отношение, б) симметричное отношение,

в) транзитивное отношение