
- •Збірник задач
- •Передмова
- •Робоча програма дисципліни «Фізика»
- •Як правильно оформляти задачі і контрольну роботу в цілому?
- •Київський національний Університет Будівництва і архітектури Кафедра фізики
- •Модуль 1 «Механіка»
- •1.1. Короткий теоретичний довідник до модуля 1.
- •1.2. Задачі до модуля 1
- •Модуль 2 «Молекулярна фізика»
- •2.1. Короткий теоретичний довідник до модуля 2
- •2.2. Задачі до модуля 2
- •Модуль 3 «Електрика та магнетизм»
- •3.1. Короткий теоретичний довідник до модуля 3
- •3.2. Задачі до модуля 3
- •Модуль 4 «Коливальні та хвильові процеси, оптика»
- •4.1. Короткий теоретичний довідник до модуля 4
- •4.1.А. Короткий теоретичний довідник до теми «Геометрична оптика»
- •4.2. Задачі до модуля 4
- •4.2.А. Задачі до теми «Геометрична оптика»
- •Модуль 5 «Основи квантової фізики та фізики ядра»
- •5.1. Короткий теоретичний довідник до модуля 5
- •5.2. Задачі до модуля 5
- •Список літератури
- •Основні одиниці Міжнародної системи (сі)
- •Основні фізичні сталі
- •Деякі позасистемні величини
- •Деякі співвідношення між фізичними величинами
- •Деякі астрономічні величини
- •Властивості деяких твердих тіл
- •Властивості деяких рідин
- •Густина газів (за нормальних умов), кг/м3
- •Густина (середня насипна) деяких будівельних матеріалів, кг/м3
- •Густина деяких речовин і матеріалів, кг/м3
- •Пружні властивості деяких твердих тіл
- •Модуль Юнга деяких матеріалів, Гпа
- •Границя міцності деяких матеріалів, Гпа
- •Залежність відносних долей молекул за розподілом Максвела від відносної швидкості
- •Залежність долі молекул, швидкості яких перевищують задане значення відносної швидкості
- •Питома теплота згоряння деяких видів палива, мДж/кг
- •Питома теплота плавлення і температура плавлення деяких речовин, металів та сплавів (за нормального атмосферного тиску)
- •Температурний коефіцієнт лінійного розширення деяких речовин
- •Питома теплота пароутворення води при різних температурах
- •Критичні значення температури та тиску для деяких речовин
- •Діелектрична проникність деяких речовин
- •Робота виходу електронів з металів
- •Маса і енергія спокою деяких частинок
- •Маса деяких нуклідів, а.О.М.
- •Енергія іонізації
- •Десяткові префікси до назв одиниць
- •Графік залежності коефіцієнта поглинання -випромінювання від енергії падаючого кванта для різних речовин
Модуль 3 «Електрика та магнетизм»
3.1. Короткий теоретичний довідник до модуля 3
Взаємодія точкових
зарядів визначається законом Кулона
 ,
де –q1
і q2
– величина зарядів, r
–
відстань між зарядами,
,
де –q1
і q2
– величина зарядів, r
–
відстань між зарядами,
![]() –
діелектрична проникність середовища,
–
діелектрична проникність середовища,
![]()
електрична стала. Напруженість і
потенціал електричного поля:
електрична стала. Напруженість і
потенціал електричного поля:
 ,
,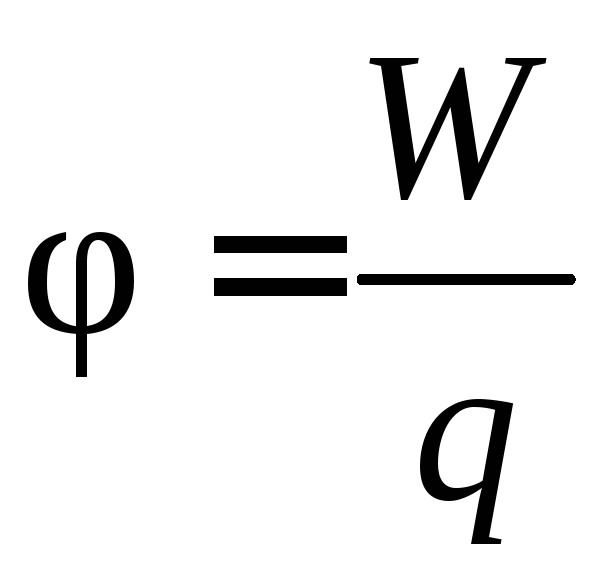 ,
деW–
потенціальна енергія точкового
позитивного заряду q,
який перебуває у даній точці поля.
Принцип суперпозиції електричних полів:
,
деW–
потенціальна енергія точкового
позитивного заряду q,
який перебуває у даній точці поля.
Принцип суперпозиції електричних полів:
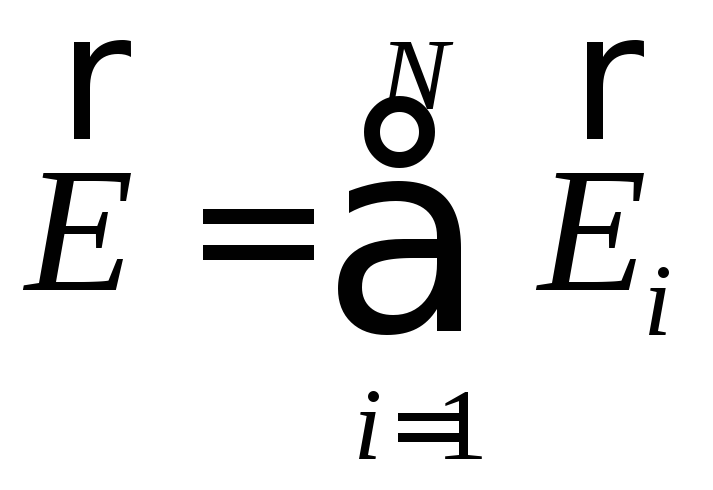 ,
, ,
деЕi,
,
деЕi,
![]() –
напруженість і потенціал у даній точці
поля, створені i
– м зарядом. Для точкового заряду
напруженість та потенціал електричного
поля:
–
напруженість і потенціал у даній точці
поля, створені i
– м зарядом. Для точкового заряду
напруженість та потенціал електричного
поля:
 ,
,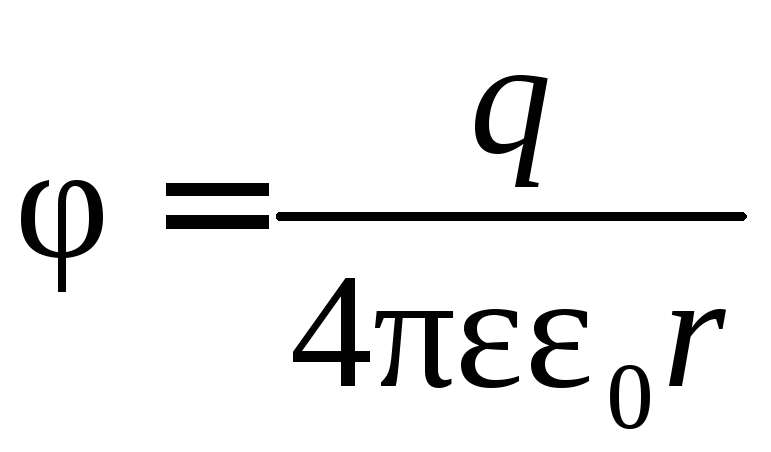 ,де r – відстань
від заряду q
до точки, в якій визначається напруженість
і потенціал. Робота сил електричного
поля по переміщенню заряду q
визначається через різницю потенціалів:
A=q(φ1-
φ2).
Зв’язок потенціалу з напруженістю
електричного поля:
,де r – відстань
від заряду q
до точки, в якій визначається напруженість
і потенціал. Робота сил електричного
поля по переміщенню заряду q
визначається через різницю потенціалів:
A=q(φ1-
φ2).
Зв’язок потенціалу з напруженістю
електричного поля:
![]() .
.
Теорема Гаусса
 ,
де замкнена поверхняS
охоплює
електричні заряди qi.
За т. Гаусса напруженість електричного
поля, створеного нескінченною прямою
рівномірно зарядженою ниткою або
нескінченно довгим циліндром:
,
де замкнена поверхняS
охоплює
електричні заряди qi.
За т. Гаусса напруженість електричного
поля, створеного нескінченною прямою
рівномірно зарядженою ниткою або
нескінченно довгим циліндром:
![]() ,
де
,
де![]() – лінійна густина заряду,r
– відстань від нитки або осі циліндра
до точки, у якій визначається напруженість
поля. Напруженість електричного поля,
яке створюється нескінченною, рівномірно
зарядженою площиною:
– лінійна густина заряду,r
– відстань від нитки або осі циліндра
до точки, у якій визначається напруженість
поля. Напруженість електричного поля,
яке створюється нескінченною, рівномірно
зарядженою площиною:
![]() ,
де
,
де![]() –
поверхнева густина зарядів.
–
поверхнева густина зарядів.
Електричний момент
диполя
![]() ,
де q – заряд
, l
– плече диполя. Обертальний момент, що
діє на диполь в електричному полі
,
де q – заряд
, l
– плече диполя. Обертальний момент, що
діє на диполь в електричному полі
![]() ,
а додаткова потенціальна енергія диполя
,
а додаткова потенціальна енергія диполя![]() .
.
Електроємність
провідника С=q/Δφ,
або конденсатора C=q/U,
де Δφ – зміна потенціалу поверхні
провідника, U
– різниця потенціалів між пластинами
конденсатора. Електроємність окремої
провідної сфери радіусом R:
![]() .
Електроємність плоского конденсатора:
.
Електроємність плоского конденсатора: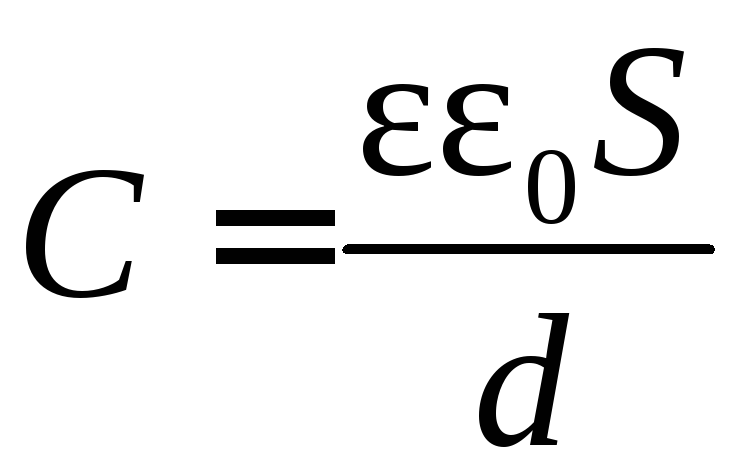 ,
деS
– площа однієї пластини конденсатора,
d
– відстань між пластинами. Електроємність
батареї конденсаторів:
,
деS
– площа однієї пластини конденсатора,
d
– відстань між пластинами. Електроємність
батареї конденсаторів:
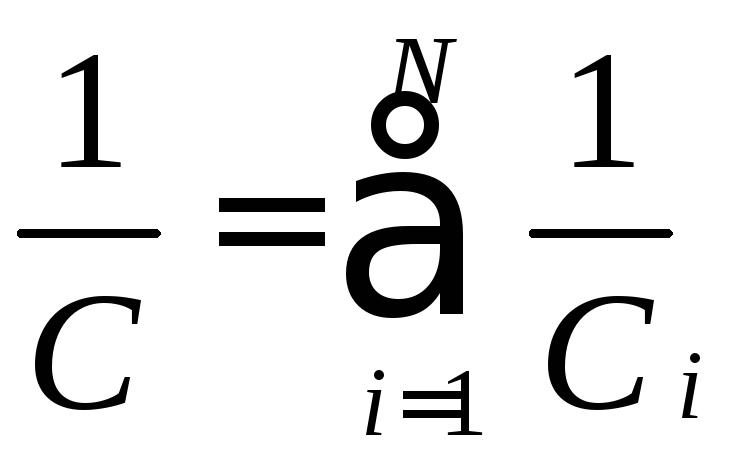 –
для послідовного з’єднання,
–
для послідовного з’єднання,
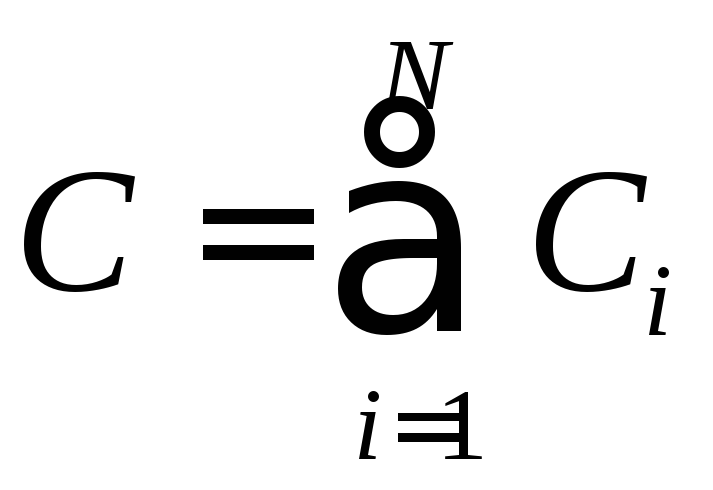 – для паралельного з’єднання, деN
– кількість конденсаторів у батареї.
Енергія зарядженого конденсатора:
– для паралельного з’єднання, деN
– кількість конденсаторів у батареї.
Енергія зарядженого конденсатора:
![]() .
.
Сила струму
![]() ,
густина струму
,
густина струму ,
деS
– площина поперечного перерізу
провідника, Закон Ома визначає силу
струму в однорідній ділянці кола
,
деS
– площина поперечного перерізу
провідника, Закон Ома визначає силу
струму в однорідній ділянці кола
 ,
деU
– різниця потенціалів (напруга) на
кінцях ділянки, R
– електричний опір ділянки. Закон Ома
для замкненого кола
,
деU
– різниця потенціалів (напруга) на
кінцях ділянки, R
– електричний опір ділянки. Закон Ома
для замкненого кола
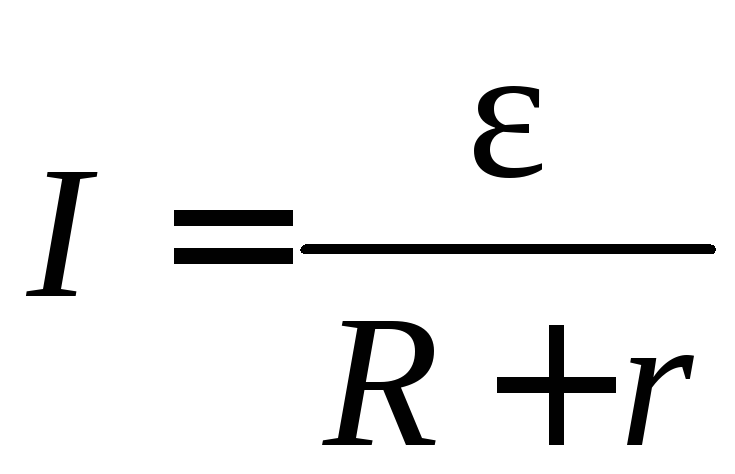 ,
деЕ
– ЕРС джерела струму. R
– зовнішній опір кола, r
– внутрішній опір джерела струму.
Правила Кірхгофа для розрахунку складних
кіл:
,
деЕ
– ЕРС джерела струму. R
– зовнішній опір кола, r
– внутрішній опір джерела струму.
Правила Кірхгофа для розрахунку складних
кіл:
 – перше правило для вузлів електричної
схеми,
– перше правило для вузлів електричної
схеми,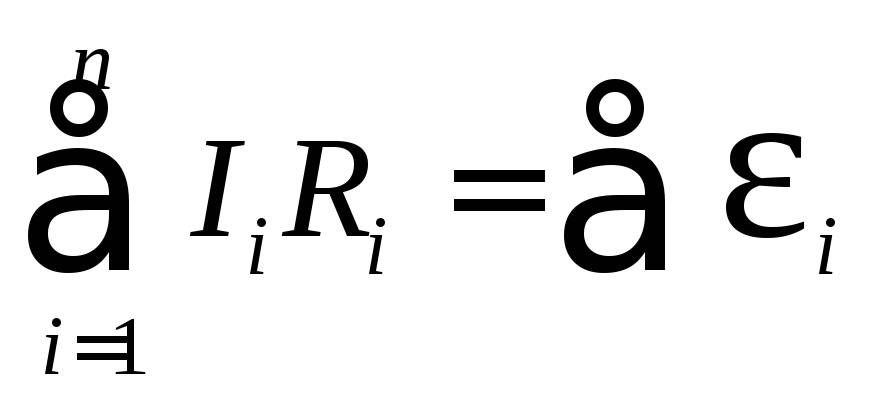 –
друге правило для замкнених контурів.
Опір провідника
–
друге правило для замкнених контурів.
Опір провідника ,
де ρ ‑ питомий опір матеріалу
провідника,l
– довжина
провідника, S – площа
поперечного перерізу. Опір системи
провідників:
,
де ρ ‑ питомий опір матеріалу
провідника,l
– довжина
провідника, S – площа
поперечного перерізу. Опір системи
провідників:
 –
для послідовного з’єднання,
–
для послідовного з’єднання,
 – для паралельного з’єднання, деRi
– опір і-го
провідника.
– для паралельного з’єднання, деRi
– опір і-го
провідника.
При протіканні
струму через електроліт на електродах
виділяється маса речовини, що визначається
законом Фарадея для електролізу:
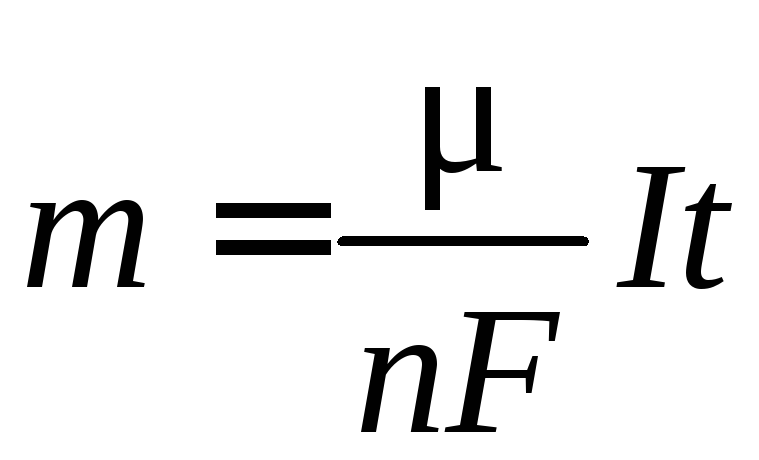 ,
де μ – молярна маса речовини,n
– валентність, I
– сила струму, t
– час протікання струму, F
– стала Фарадея. Густина струму, що
протікає через іонізований газ:
,
де μ – молярна маса речовини,n
– валентність, I
– сила струму, t
– час протікання струму, F
– стала Фарадея. Густина струму, що
протікає через іонізований газ:
![]() ,
деq
– заряд іона, n
– концентрація іонів, u+,
u-
– рухливості іонів відповідного знака,
E
– напруженість електричного поля в
газі.
,
деq
– заряд іона, n
– концентрація іонів, u+,
u-
– рухливості іонів відповідного знака,
E
– напруженість електричного поля в
газі.
Робота струму A=IUt=I2Rt=U2t/R. Звідки потужність струму P=IU=I2R=U2/R. Закон Джоуля-Ленца: Q=I2Rt, де Q – кількість теплової енергії, що виділяється ділянкою електричного кола. Закон Ома у диференціальній формі: j=γE, де γ – питома провідність, Е – напруженість електричного поля, j – густина струму.
За законом
Біо-Савара-Лапласа вектор індукції
магнітного поля
![]() ,
створеного елементом провідника довжиноюdl
зі струмом I
чисельно дорівнює
,
створеного елементом провідника довжиноюdl
зі струмом I
чисельно дорівнює
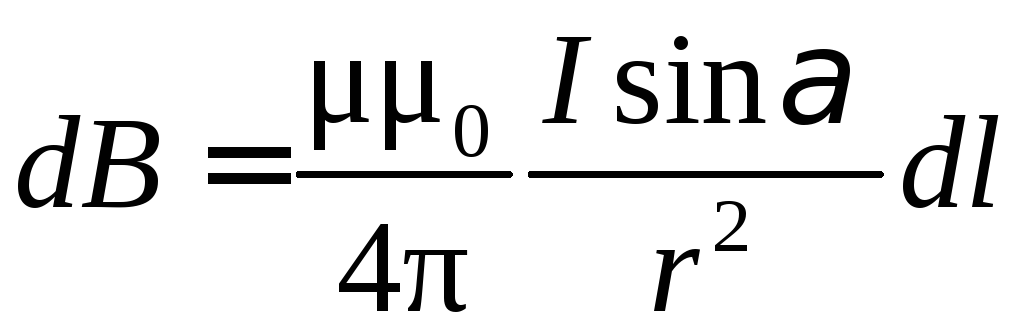 ,
де μ – магнітна проникність середовища,
μ0
– магнітна стала, r
– модуль радіус-вектора, спрямованого
від елемента провідника до точки, у якій
визначається магнітна індукція, α –
кут між радіус-вектором та напрямком
струму у елементі провідника. Зв’язок
вектора індукції з напруженістю
,
де μ – магнітна проникність середовища,
μ0
– магнітна стала, r
– модуль радіус-вектора, спрямованого
від елемента провідника до точки, у якій
визначається магнітна індукція, α –
кут між радіус-вектором та напрямком
струму у елементі провідника. Зв’язок
вектора індукції з напруженістю
![]() магнітного
поля:
магнітного
поля:![]()
![]() .
Магнітна індукція у центрі кругового
струму:
.
Магнітна індукція у центрі кругового
струму:![]() ,
деR
– радіус витка. Магнітна індукція,
створена відрізком провідника зі
струмом:
,
деR
– радіус витка. Магнітна індукція,
створена відрізком провідника зі
струмом:
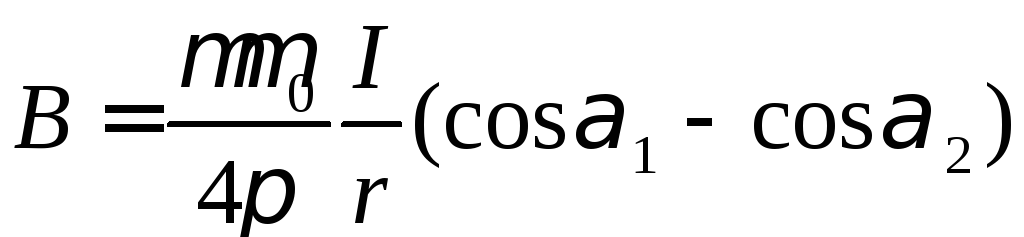 ,
де
,
де![]() ,
,![]() – кути, під якими спостерігаються кінці
відрізку з точки визначення індукції.
– кути, під якими спостерігаються кінці
відрізку з точки визначення індукції.
За законом повного
струму
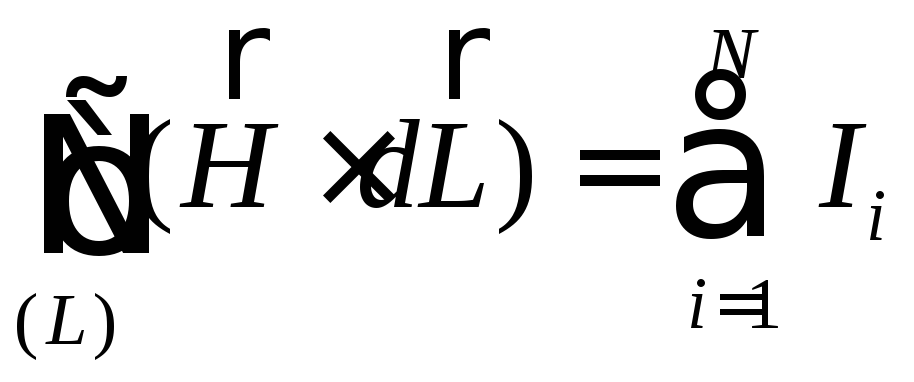 ,
деIi
–
сили струмів
у провідниках, охоплених контуром L.
Магнітна
індукція поля в середині соленоїда та
тороїда:
,
деIi
–
сили струмів
у провідниках, охоплених контуром L.
Магнітна
індукція поля в середині соленоїда та
тороїда:
![]() ,
деn
– кількість витків соленоїда на одиницю
довжини.
,
деn
– кількість витків соленоїда на одиницю
довжини.
Закон Ампера
визначає силу, що діє на провідник зі
струмом у магнітному полі:
![]() ,або
її величина
F=IBlsinα,
де l
– довжина провідника, α – кут між
напрямком струму у провіднику та вектором
магнітної індукції. Сила взаємодії
паралельних провідників зі струмом:
,або
її величина
F=IBlsinα,
де l
– довжина провідника, α – кут між
напрямком струму у провіднику та вектором
магнітної індукції. Сила взаємодії
паралельних провідників зі струмом:
 ,
деd
–
відстань між провідниками.
,
деd
–
відстань між провідниками.
Магнітний момент
плоского контура зі струмом:
![]() ,
де
,
де![]() –
одиничний вектор нормалі до площин
контура, I
–
сила струму, S
–
площа контура. Обертальний момент, що
діє на контур зі струмом у однорідному
магнітному полі:
–
одиничний вектор нормалі до площин
контура, I
–
сила струму, S
–
площа контура. Обертальний момент, що
діє на контур зі струмом у однорідному
магнітному полі:
![]() або за величиною
або за величиною![]() ,
де α–
кут між векторами
,
де α–
кут між векторами
![]() та
та![]() .
.
Сила Лоренца, що
діє на рухомий заряд в магнітному полі
![]() .
За величиною
.
За величиною![]() ,
де
,
де![]() - швидкість зарядженої частинки, α
– кут між
векторами
- швидкість зарядженої частинки, α
– кут між
векторами
![]() та
та![]() .
.
Магнітний потік, що перетинає контур зі струмом: Ф=BScos α, де S – площа контура, α – кут між нормаллю до площини контура та вектором магнітної індукції. Робота по переміщенню замкнутого контура у магнітному полі: А=I∆Ф.
Явище електромагнітної
індукції описується законом Фарадея:
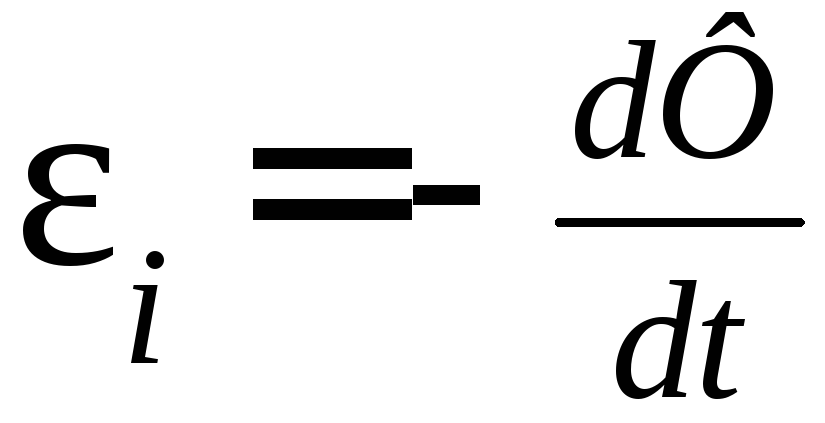 .
Різниця потенціалів на ділянці провідника,
що рухається у магнітному полі: U=B
.
Різниця потенціалів на ділянці провідника,
що рухається у магнітному полі: U=B![]() lsinα,
де υ
– швидкість руху провідника, α
– кут між векторами
lsinα,
де υ
– швидкість руху провідника, α
– кут між векторами
![]() та
та![]() .
Явище самоіндукції описується законом
Генрі:
.
Явище самоіндукції описується законом
Генрі:
 ,
де L
– індуктивність
контура. Індуктивність соленоїда
,
де L
– індуктивність
контура. Індуктивність соленоїда
![]() ,
де n
– кількість витків на одиниці довжини,
V
– об’єм
соленоїда.
,
де n
– кількість витків на одиниці довжини,
V
– об’єм
соленоїда.
Миттєве значення
сили струму у колі, яке має опір R
та індуктивність L:
 –
для замикання кола, де
–
для замикання кола, де
![]() – ЕРС джерела струму, t
–
час після замикання кола;
– ЕРС джерела струму, t
–
час після замикання кола;
![]() – для розмикання кола, деI0
– струм у колі
для t
=
0.
– для розмикання кола, деI0
– струм у колі
для t
=
0.
Енергія магнітного
поля контура зі струмом:
 .
Об’ємна
густина енергії магнітного поля:
.
Об’ємна
густина енергії магнітного поля:
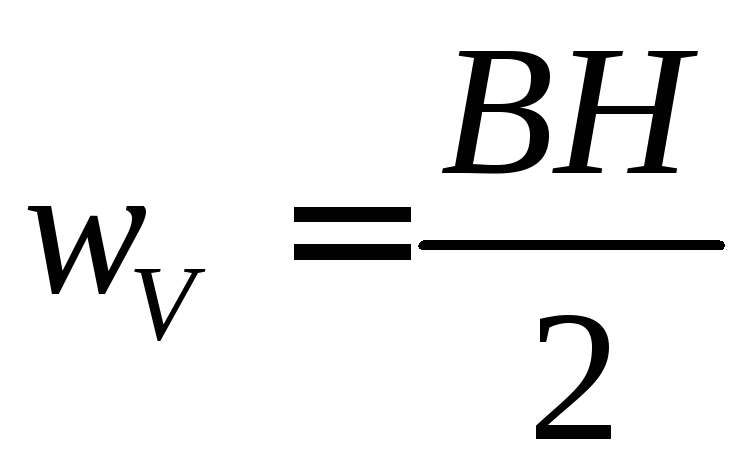 ,
де B
–
магнітна
індукція, Н
–
напруженість
магнітного поля. Зокрема для соленоїда
енергія магнітного поля:
,
де B
–
магнітна
індукція, Н
–
напруженість
магнітного поля. Зокрема для соленоїда
енергія магнітного поля:
 ,де S
–
площа поперечного перерізу, l
–
довжина соленоїда.
,де S
–
площа поперечного перерізу, l
–
довжина соленоїда.
