Модель межотраслевого баланса

Пример

В таблице приведена структура трехотраслевой экономики в единицах стоимости.

Отрасли	1	2	3	Конечный спрос	Валовой выпуск
				yi	xi
1	27	13	30	80	150
2	19	28	16	60	123
3	21	29	30	90	170

Здесь y_i – объем продукции отрасли i, потребляемый в непроизводственной сфере. В него входят личное потребление, обеспечение общественных потребностей, поставки на экспорт;

x_i – валовой выпуск продукции i-й отрасли;

x_ij – объем продукции отрасли i, расходуемый отраслью j – производственное потребление.

Вычислить вектор валового выпуска и значения межотраслевых потоков продукции для заданного вектора конечного спроса Y^T = [100, 80, 110].

Решение.

Рассчитаем матрицу А прямых затрат на единицу общего выпуска продукции (a_ij = x_ij / x_{j, i, j} = 1, 2, 3)

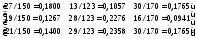
Коэффициенты a_ij матрицы А указывают, что для производства валовой продукции j-й отрасли на сумму в одну стоимостную единицу (например, 1 млрд руб.) необходимо использовать объем валовой продукции i-й отрасли на сумму a_ij стоимостных единиц.

Затем вычисляем матрицу полных затрат B как матрицу, обратную к матрице Е – А:

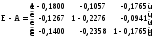
Коэффициенты b_ij матрицы В показывают, что для производства конечной продукции j-й отрасли на сумму в одну единицу стоимости необходимо израсходовать валовой продукции i-й отрасли на сумму b_ij единиц.

Находим искомый объем валового выпуска для данного конечного спроса:

Получим значения межотраслевых потоков продукции, умножая элементы i-го столбца матрицы прямых затрат A на i-ю строку вектора общего выпуска X:

Отрасли	1	2	3	Конечный спрос	Валовой выпуск
				yi	xi
1	0,1800 · 188,0950 = = 33,8571	0,1057 · 160,1883= = 16,9305	0,1765 · 211,4087= = 37,3074	100	188,0950
2	0,2167 · 188,0950 = = 23,8254	0,2276 · 160,1883= = 36,4656	0,0941 · 211,4087= = 19,8973	80	160,1883
3	0,1400 · 188,0950 = = 26,3333	0,2358 · 160,1883= = 37,7680	0,1765 · 211,4087= = 37,3074	110	211,4087

Для контроля правильности вычислений можно просуммировать построчно производственное потребление и конечный спрос. Эти суммы должны совпадать с валовым выпуском.

Задачи

Для заданных моделей трехотраслевой экономики и для заданного вектора конечного спроса Y рассчитать межотраслевой баланс производства и распределения продукции.

1

Отрасли	1	2	3	Конечный спрос	Валовой выпуск
1	15	20	27	50	112
2	21	17	20	80	138
3	13	15	10	60	98

Y^T = [63, 100, 80].

2

Отрасли	1	2	3	Конечный спрос	Валовой выпуск
1	23	18	32	70	143
2	35	27	23	90	175
3	16	13	11	50	90

Y^T = [90, 100, 70].

3

Отрасли	1	2	3	Конечный спрос	Валовой выпуск
1	21	14	15	60	110
2	17	19	10	50	96
3	22	20	14	80	136

Y^T = [70, 72, 94].

4

Отрасли	1	2	3	Конечный спрос	Валовой выпуск
1	25	15	30	80	150
2	19	32	21	90	162
3	16	14	15	60	105

Y^T = [100, 110, 90].

5

Отрасли	1	2	3	Конечный спрос	Валовой выпуск
1	11	15	10	40	76
2	23	16	21	70	130
3	14	22	15	60	111

Y^T = [60, 80, 80].