Учреждение образования
«Частный институт управления и предпринимательства»
В.А. Шкель
ЭКОНОМЕТРИКА
И ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ
МЕТОДЫ И МОДЕЛИ
Сборник задач
Учебно-методическое пособие
Минск
2013
УДК 519.2
ББК 22.173
Ш66
Рекомендовано к изданию редакционно-издательским советом
Частного института управления и предпринимательства
А в т о р
доцент кафедры высшей математики и статистики
Частного института управления и предпринимательства
кандидат физико-математических наук,
старший научный сотрудник В.А. Шкель
Р е ц е н з е н т ы:
доцент кафедры высшей математики БГУИР кандидат физико-математических наук, доцент В.М. Метельский;
доцент кафедры управления финансами ГИУСТ БГУ кандидат физико-математических наук, доцент Н.Н. Рачковский
Рассмотрено и одобрено
на заседании кафедры высшей математики и статистики,
протокол № 10 от 12.04.2013 г.
Шкель, В.А.
Ш66 Эконометрика и экономико-математические методы и модели: сборник задач: учеб.-метод. пособие / В.А. Шкель – Минск: Частн. ин-т упр. и предпр., 2013. – 36 с.
ISBN 978-985-6971-89-4.
Рассматриваются примеры решения задач по эконометрике и ЭМММ, приведены задания для использования в учебном процессе и для самостоятельной работы.
Пособие предназначено для студентов дневной и заочной форм обучения Частного института управления и предпринимательства.
УДК 519.2
ББК 22.173
ISBN 978-985-6971-89-4 © Шкель В.А., 2013
©
Частный институт управления и
предпринимательства, 2013
Содержание
Линейная парная регрессия 4
Модель множественной регрессии 7
Матричные игры 11
Системы массового обслуживания (СМО) 19
Модели сетевого планирования и управления 23
Модель межотраслевого баланса 30
Список литературы 33
Линейная парная регрессия
Пример. В таблице приведены данные о двух условных экономических показателях x и y.
|
x |
2,0 |
2,1 |
2,3 |
2,4 |
2,9 |
3,3 |
3,8 |
4,6 |
|
y |
14,3 |
18,6 |
18,7 |
20,9 |
22,3 |
24,2 |
25,7 |
27,0 |
Необходимо:
1) оценить степень тесноты связи между переменными с помощью коэффициента корреляции;
2) построить уравнение линейной регрессии;
3) вычислить среднюю ошибку аппроксимации.
Решение
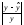
Для оценки силы линейной зависимости между переменными x и y вычислим коэффициент корреляции rxy по формуле
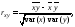
где 
![]()
![]()
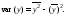
![]()
Вычисления сведем в таблицу:
|
№ |
x |
y |
x2 |
y2 |
xy |
|
1 |
2,0 |
14,3 |
4,00 |
204,49 |
28,60 |
|
2 |
2,1 |
18,6 |
4,41 |
345,96 |
39,06 |
|
3 |
2,3 |
18,7 |
5,29 |
349,69 |
43,01 |
|
4 |
2,4 |
20,9 |
5,76 |
436,81 |
50,16 |
|
5 |
2,9 |
22,3 |
8,41 |
497,29 |
64,67 |
|
6 |
3,3 |
24,2 |
10,89 |
585,64 |
79,86 |
Окончание таблицы
|
№ |
x |
y |
x2 |
y2 |
xy |
|
7 |
3,8 |
25,7 |
14,44 |
660,49 |
97,66 |
|
8 |
4,6 |
27,0 |
21,16 |
729,00 |
124,20 |
|
Сумма |
23,4 |
171,7 |
74,36 |
3809,37 |
527,22 |
|
Среднее |
2,92 |
21,46 |
9,29 |
476,17 |
65,90 |
Подставляя значения в формулу, получим:
var
(x)
= 9,29 –
2,922
= 0,74;![]()
var ( y) = 476,17 – 21,462 = 15,64;
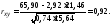
![]()
Так как коэффициент
корреляции близок к единице, то между
переменными x![]() и y
и y
![]() существует
достаточно выраженная линейная
зависимость.
существует
достаточно выраженная линейная
зависимость.
Для построения
линейного уравнения регрессии
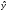 = a
+
bx
коэффициенты a
и b
находим по формулам:
= a
+
bx
коэффициенты a
и b
находим по формулам:

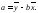
Подставляя значения, получим:
a = 21,46 – 4,38 · 2,92 = 8,67;
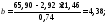
 = 8,67 + 4,38
· x.
= 8,67 + 4,38
· x.
Средняя ошибка аппроксимации вычисляется по формуле

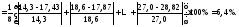
![]()


![]() Так
как средняя ошибка аппроксимации меньше
10%, уравнение регрессии может использоваться
для исследования зависимости между
переменными.
Так
как средняя ошибка аппроксимации меньше
10%, уравнение регрессии может использоваться
для исследования зависимости между
переменными.
Задачи
Для переменных, заданных в таблицах, оценить степень тесноты связи между переменными, построить уравнение линейной регрессии и вычислить среднюю ошибку аппроксимации.
1
|
x |
3,3 |
3,5 |
2,5 |
3,9 |
3,6 |
1,8 |
3,4 |
2,3 |
|
y |
67 |
66 |
70 |
61 |
63 |
75 |
65 |
69 |
2
|
x |
21 |
25 |
25 |
19 |
28 |
35 |
34 |
39 |
|
y |
14 |
17 |
17 |
15 |
25 |
28 |
28 |
34 |
3
|
x |
1,5 |
2,1 |
2,6 |
2,9 |
3,8 |
4,8 |
5,8 |
5,6 |
|
y |
28 |
29 |
44 |
52 |
69 |
77 |
82 |
90 |
4
|
x |
5,6 |
5,8 |
4,8 |
6,3 |
6,0 |
4,0 |
5,8 |
4,5 |
|
y |
79 |
75 |
86 |
73 |
70 |
80 |
75 |
77 |
5
|
x |
1,4 |
2,2 |
2,5 |
2,8 |
3,8 |
4,8 |
5,8 |
5,6 |
|
y |
28 |
30 |
41 |
52 |
69 |
77 |
81 |
85 |
Модель множественной регрессии
Пример. В таблице приведены данные трех переменных экономического содержания. Построить уравнение множественной регрессии и вычислить среднюю ошибку аппроксимации.
|
y |
10,3 |
10,5 |
10,6 |
10,7 |
11,0 |
11,5 |
12,0 |
12,2 |
|
x1 |
5 |
12 |
5 |
10 |
7 |
5 |
13 |
7 |
|
x2 |
0,85 |
0,98 |
0,82 |
0,7 |
0,53 |
0,48 |
0,61 |
0,47 |
Коэффициент уравнения
множественной регрессии
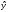 =b0
+
+ b1
x1
+ b2
x2
=b0
+
+ b1
x1
+ b2
x2
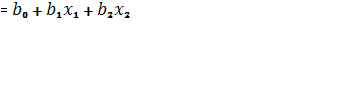 найдем
после решения системы уравнений:
найдем
после решения системы уравнений:

Вычисления сведем в таблицу:
|
№ |
y |
x1 |
x2 |
x12 |
x22 |
y2 |
x1x2 |
x1 y |
x2 y |
|
1 |
10,3 |
5 |
0,85 |
25 |
0,7225 |
106,09 |
4,25 |
51,5 |
8,755 |
|
2 |
10,5 |
12 |
0,98 |
144 |
0,9604 |
110,25 |
11,76 |
126,0 |
10,290 |
|
3 |
10,6 |
5 |
0,82 |
25 |
0,6724 |
112,36 |
4,10 |
53,0 |
8,692 |
|
4 |
10,7 |
10 |
0,70 |
100 |
0,4900 |
114,49 |
7,00 |
107,0 |
7,490 |
|
5 |
11,0 |
7 |
0,53 |
49 |
0,2809 |
121,00 |
3,71 |
77,0 |
5,830 |
|
6 |
11,5 |
5 |
0,48 |
25 |
0,2304 |
132,25 |
2,40 |
57,5 |
5,520 |
|
7 |
12,0 |
13 |
0,61 |
169 |
0,3721 |
144,00 |
7,93 |
156,0 |
7,320 |
|
8 |
12,2 |
7 |
0,47 |
49 |
0,2209 |
148,84 |
3,29 |
85,4 |
5,734 |
|
Сумма |
88,8 |
64 |
5,44 |
586 |
3,9496 |
989,28 |
44,44 |
713,4 |
59,631 |
|
Среднее |
11,1 |
8 |
0,68 |
73,25 |
0,4937 |
123,66 |
5,555 |
89,175 |
7,4539 |
Система уравнений для определения параметров b0, b1, b2:
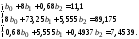
Решаем систему методом Крамера:


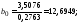



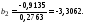
Уравнение множественной регрессии имеет вид:
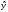 = 12,6949 +
0,0814x1
– 3,3062x2.
= 12,6949 +
0,0814x1
– 3,3062x2.
Для вычисления
средней ошибки аппроксимации вычислим
значения
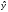
![]() ,
,![]() y
–
y
–
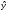
![]() ,
,
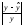
![]() :
:
|
y |
|
|
|
|
10,3 |
10,2916 |
0,0084 |
0,0008 |
|
10,5 |
10,4316 |
0,0684 |
0,0065 |
|
10,6 |
10,3908 |
0,2092 |
0,0197 |
|
10,7 |
11,1946 |
–0,4946 |
–0,0462 |
|
11,0 |
11,5124 |
–0,5124 |
–0,0466 |
|
11,5 |
11,5149 |
–0,0149 |
–0,0013 |
|
12,0 |
11,7363 |
0,2637 |
0,0220 |
|
12,2 |
11,7108 |
0,4892 |
0,0401 |
Окончательно:

Задачи
В таблицах приведены
данные о стоимости квартиры (переменная
y)
в зависимости от ее общей площади (x1![]() )
и площади кухни (
)
и площади кухни (![]() x2
x2![]() ).
Построить уравнение множественной
регрессии и вычислить среднюю ошибку
аппроксимации.
).
Построить уравнение множественной
регрессии и вычислить среднюю ошибку
аппроксимации.
1
|
y |
56 |
73 |
72 |
59 |
73 |
68 |
60 |
107 |
|
x1 |
43 |
57 |
56 |
45 |
58 |
53 |
47 |
80 |
|
x2 |
13 |
13 |
10 |
8 |
10 |
9 |
8 |
10 |
2
|
y |
61 |
77 |
76 |
62 |
77 |
72 |
62 |
113 |
|
x1 |
43 |
57 |
56 |
45 |
58 |
53 |
45 |
88 |
|
x2 |
13 |
13 |
10 |
8 |
10 |
9 |
8 |
10 |
3
|
y |
70 |
58 |
73 |
50 |
49 |
58 |
67 |
49 |
|
x1 |
55 |
46 |
57 |
37 |
37 |
44 |
53 |
37 |
|
x2 |
9 |
8 |
9 |
8 |
8 |
8 |
8 |
8 |
4
|
y |
74 |
61 |
77 |
52 |
51 |
62 |
70 |
50 |
|
x1 |
55 |
46 |
57 |
34 |
34 |
44 |
53 |
34 |
|
x2 |
9 |
8 |
9 |
8 |
8 |
8 |
6 |
7 |
5
|
y |
66 |
61 |
54 |
97 |
58 |
53 |
101 |
44 |
|
x1 |
58 |
57 |
46 |
83 |
48 |
46 |
88 |
37 |
|
x2 |
10 |
9 |
8 |
10 |
9 |
8 |
25 |
6 |