Критерий отрицательной определенности
Для того чтобы квадратичная форма (х) = хТАх была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного – отрицательны, то есть:
М1 < 0, M2 > 0, М3 < 0, …, (–1)n Mn > 0.
ПРИМЕР 3.
При каких значениях а и в квадратичная форма будет положительно определенной?
(х1,
х2,
x3)
=
Решение.
Построим матрицу А и найдем ее главные миноры.
М1
= 1 > 0,
=
а
– 1 > 0
а
> 1.
=
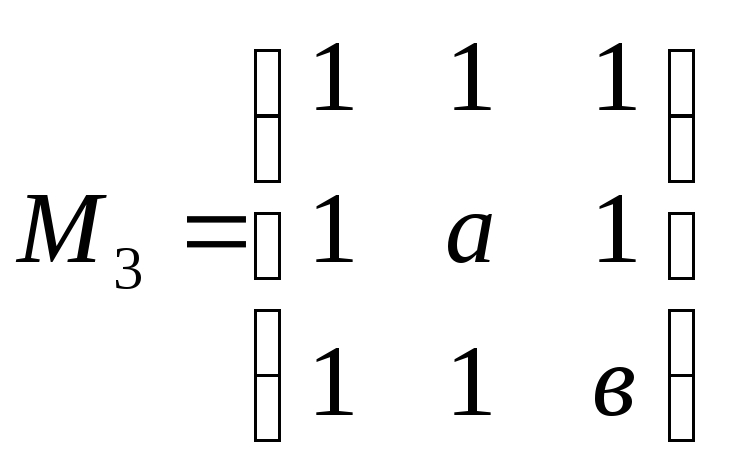ав – а – в >
0
в
>
.
Ответ:
а
> 1, в
>
.
ПРИМЕР 4.
При каких значениях а и в квадратичная форма будет отрицательно определенной?
(х1,
х2,
x3)
=
Решение.
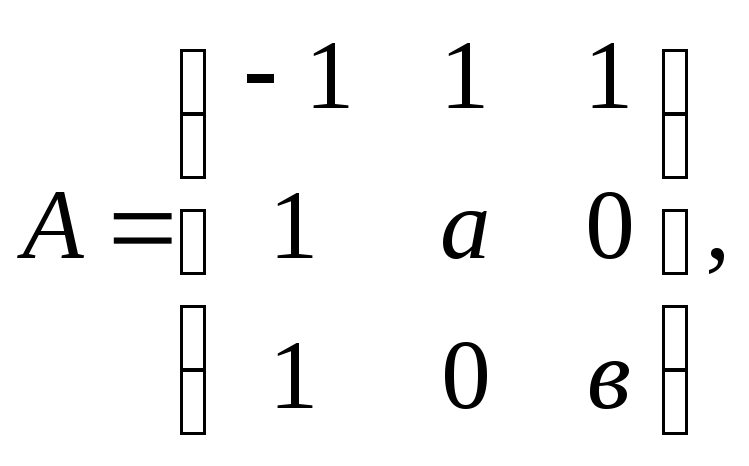М1
= –1 < 0,
=
–а
– 1 > 0
а
< –1.
=
–ав – а – в
< 0
в
> –
.
Ответ:
а
< –1, в
> –
.
ПРИМЕР 5.
Доказать,
что квадратичная форма
(х1,
х2,
x3)
=
положительно определена.
Решение.
Воспользуемся критерием Сильвестра. Построим матрицу А и найдем главные миноры матрицы А.
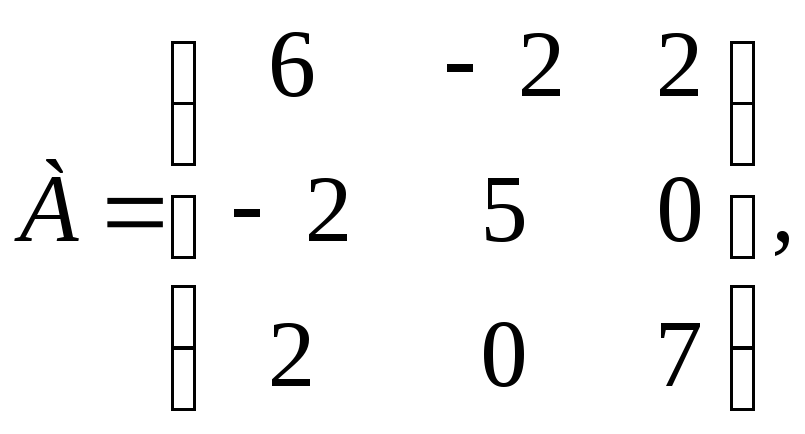
М1
= 6 > 0,
= 26 > 0,М3
=
А
= 162 > 0
(х1, х2, x3) положительно определенная квадратичная форма.
Задачи и упражнения
Какое множество точек на плоскости определяет уравнение х2 + у2 – – 4х + 10у + 29 = 0?
Найти координаты центра и радиус окружности, определяемой уравнением х2 – 6х + у2 + 12у + 36 = 0.
Записать каноническое уравнение эллипса, проходящего через точки
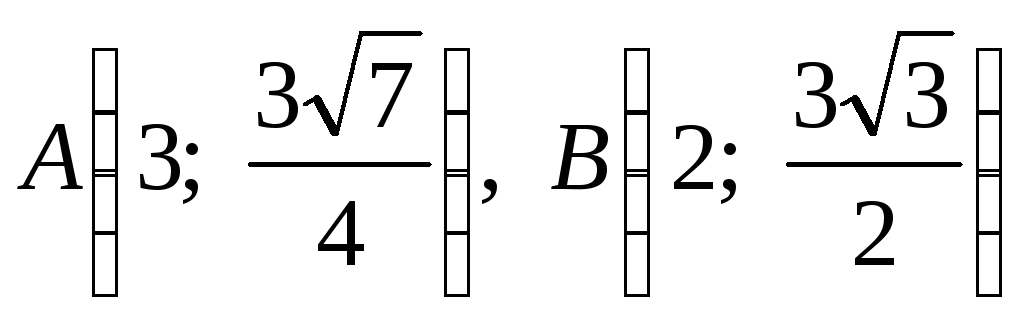.Найти фокусы и эксцентриситет эллипса 3х2 + 4у2 = 12.
Какую линию определяет уравнение 9х2 – 4у2 = 36. Найти фокусы и эксцентриситет.
Найти полуоси, координаты фокусов и эксцентриситет гиперболы, заданной уравнением 5х2 – 4у2 = 20.
Записать уравнение асимптот и директрис гиперболы 4х2 – 9у2 = 36.
Большая ось эллипса равна 12, а директрисами его служат прямые х = 18. Составить уравнение эллипса.
Найти полуоси, составить уравнения асимптот и директрис гиперболы 3х2 – 4у2 = 12.
Найти координаты фокуса и уравнение директрисы параболы у2 = 8х.
Найти координаты фокуса и уравнение директрисы параболы х2 = 4у. Вычислить расстояние от точки М(6; 9) до фокуса.
Составить уравнение гиперболы, зная, что расстояние между ее директрисами равно 4, а расстояние между фокусами 16.
Найти координаты фокусов, эксцентриситет, уравнения асимптот и директрис гиперболы 9х2 – 16у2 = 144.
Найти координаты фокуса и уравнение директрисы параболы у2 = 12х. определить расстояние от точки М(3; 6) до фокуса.
Записать матрицу квадратичной формы (х1, х2, x3) =
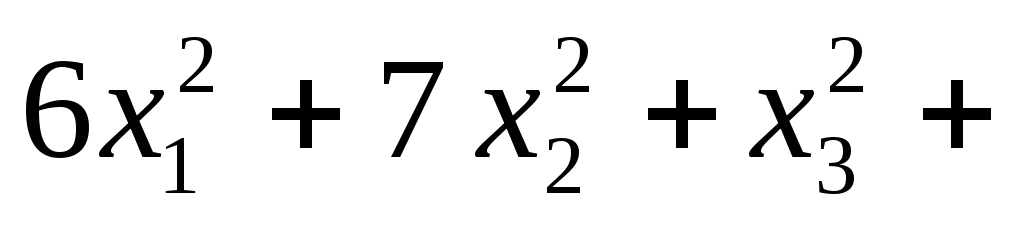
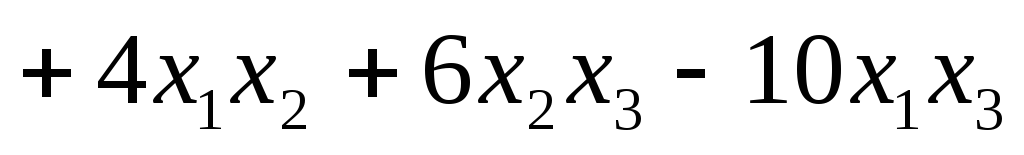.Определить знакоопределенность квадратичных форм.
а)
(х1,
х2,
x3)
=
,
б)
(х1,
х2,
x3)
=
.
ОТВЕТЫ
Точка М (2; -5).
М (3; -6), R = 3.
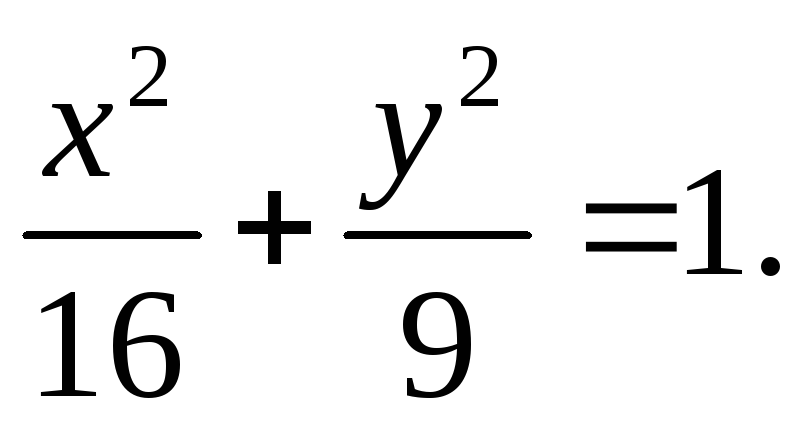
F1 (-1; 0), F2 (1; 0), = 0,5.
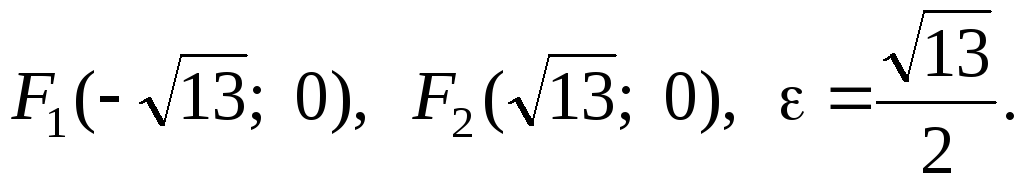
а = 2, в =
,F1
(-3; 0),
F2
(3; 0),
= 1,5.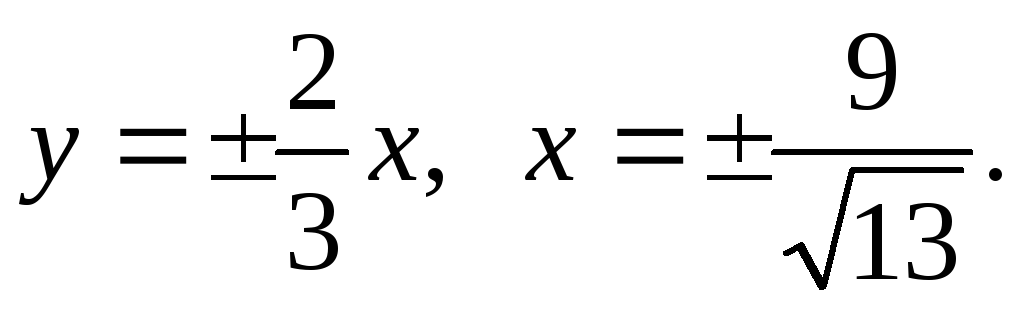
а = 2, в =
,
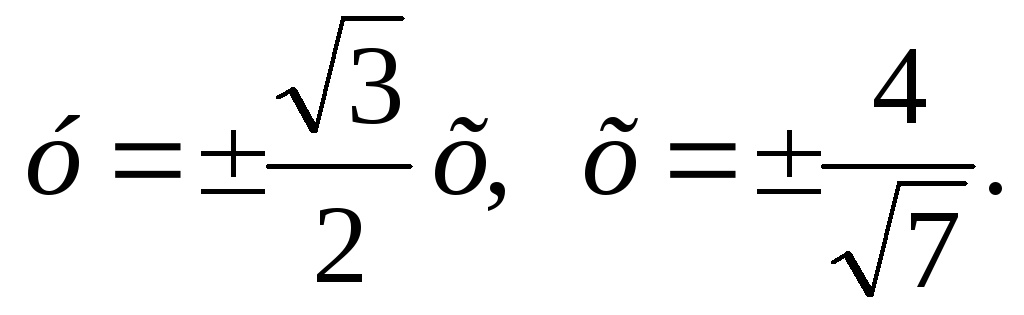
F (2; 0), х = -2.
F (0; 2), у = -2, r = 10.
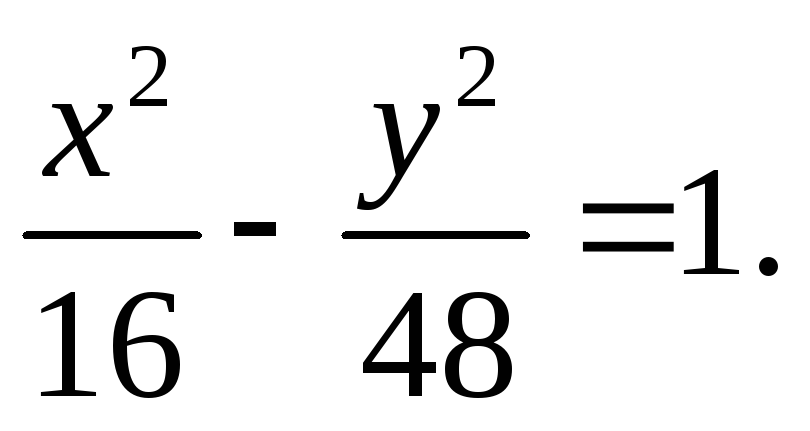
F1 (-5; 0), F2 (5; 0), =
,
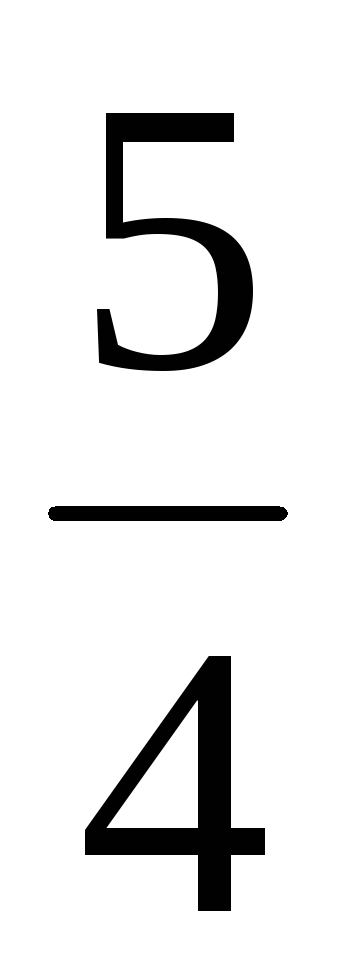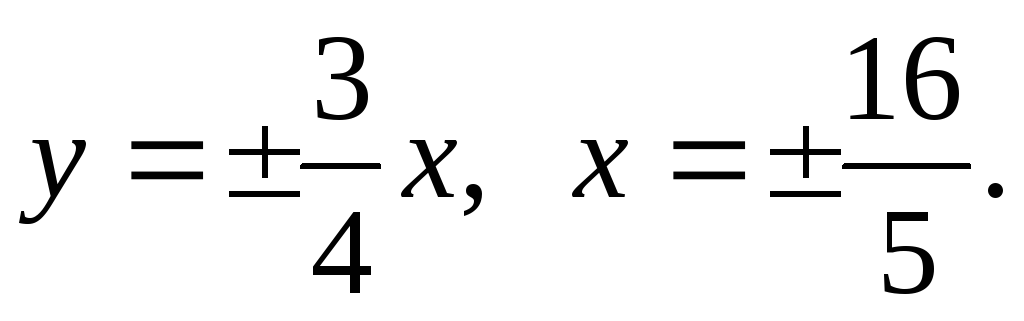
F (3; 0), х = -3, r = 6.
а) положительно определена, б) квадратичная форма не является знакоопределенной.
