- •2. Геометричні характеристики плоских перерізів
- •2.1. Основні геометричні характеристики
- •Плоских перерізів
- •2.2. Моменти інерції простих поперечних перерізів
- •2.3. Моменти інерції відносно паралельних осей
- •2.4. Визначення напряму головних осей інерції Головні моменти інерції
- •2.5. Порядок виконання розрахунків
- •2.6. Приклади
- •2.7. Завдання для виконання розрахункової роботи
- •Питання для самоконтролю
2.6. Приклади
Приклад 1. Для перерізу, складеного з двох швелерів № 40, розміщених на відстані 20 см один від одного, визначити момент опору відносно головних центральних осей u і v.
Виписуємо необхідні геометричні характеристики для швелера №40 із таблиці сортаменту ГОСТ 8239-72, ГОСТ 8510-72:
![]()
![]()
![]()
![]()
Креслимо у масштабі заданий складний переріз (рис. 2.7)
Позначаємо власні осі простих перерізів, відносно яких осьові моменти
|
інерції знаходяться в таблицях сортаменту (див. додаток). Даний складний переріз має дві осі симетрії, які співпадають з головними центральними осями. Проводимо головні центральні осі u і v. 3. Центр ваги даного складного перерізу лежить на перетині головних центральних осей 4. Визначаємо осьові моменти інерції складного перерізу відносно |
|
головних центральних осей u і v, користуючись формулою переходу до паралельних осей.
Вісь хо простих перерізів співпадає з віссю и, тому момент інерції складного перерізу відносно цієї осі дорівнює:
![]() .
.
Вісь уо простих поперечних перерізів не збігається з віссю v, тому треба скористатися формулою переходу до паралельних осей:
![]() .
.
5. Визначаємо радіуси інерції складного перерізу відносно головних центральних осей u та v:
![]() ;
;
![]() .
.
Визначаємо моменти опору складного перерізу відносно головних центральних осей u та v:
![]() ;
;
![]() .
.
Таким чином мінімальним моментом опору буде Wv , а мінімальним радіусом інерції iv.
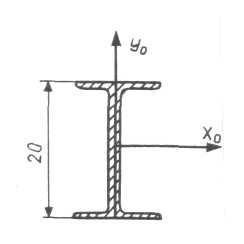
Приклад 2. Для поперечного перерізу, складеного з двотавра № 20 та швелера № 30 визначити радіуси інерції відносно головних центральних осей.
Із таблиць сортаменту ГОСТ 8239-72, ГОСТ 8240-72 визначаємо необхідні геометричні характеристики для двотавра і швелера.
|
|
№ 20 |
|
|
|
№ 30 |
|
2. Креслимо складний поперечний переріз у масштабі (рис. 2.8).
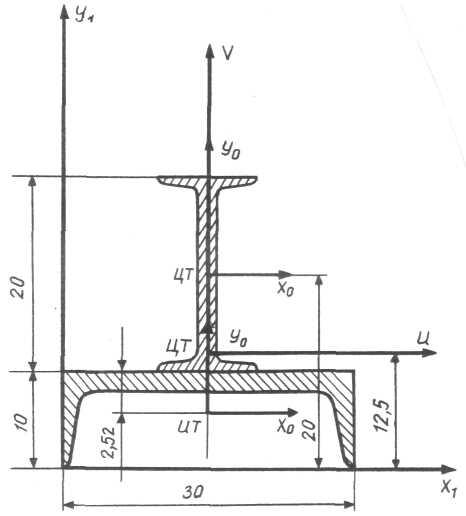
Рис. 2.8. Переріз швелера та двотавра
3. Показуємо координати центрів ваги простих поперечних перерізів у системі допоміжних осей х1 та у1.
Цей складний переріз має одну вісь симетрії, тому одна координата центра ваги вже відома. Вона дорівнює хцт = 15 см.
4. Визначаємо другу координату центра ваги, використовуючи формулу (2.3).
Показуємо центр ваги складного поперечного перерізу і головні центральні осі u та v (рис. 2.8).
Визначаємо головні центральні моменти складного перерізу. Вісь v співпадає з осями у0 простих поперечних перерізів. Тому:
![]()
Вісь u не співпадає з осями xо простих поперечних перерізів, тому треба використати формулу переходу до паралельних осей (2.11):
![]()
![]()
![]() .
.
6. Визначаємо моменти опору даного перерізу відносно головних центральних осей (формула 2.8):
![]()
![]()
7. Визначаємо радіуси інерції по формулі 2.10:
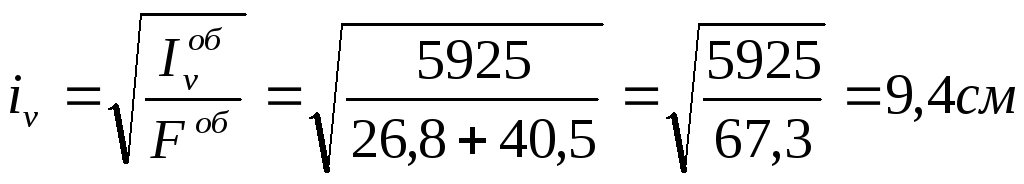 ;
;
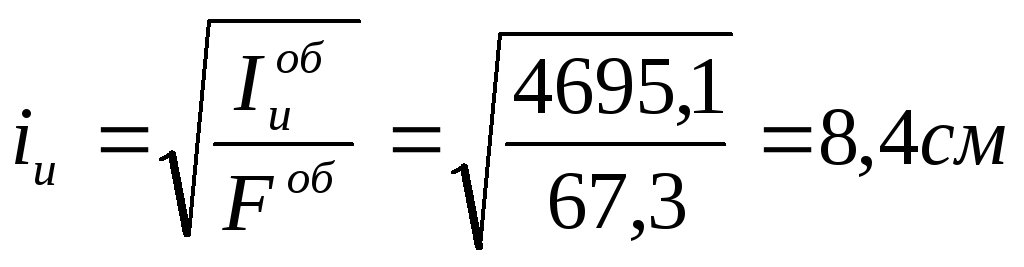 .
.
Таким
чином:
![]() ,
,![]() .
.
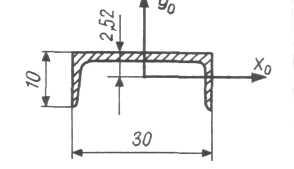
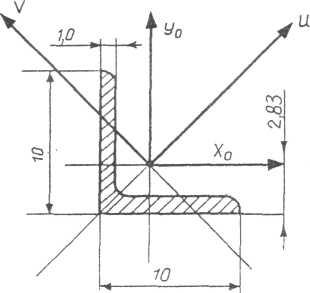
Приклад 3. Обчислити мінімальний радіус інерції складного поперечного перерізу, який складається із швелера № 20а та рівнополичного кутника розміром 100x100x10 мм.
1. Виписуємо необхідні геометричні характеристики прокатних профілів із таблиць сортаменту ГОСТ 8240-89 і 8509-86.
|
|
|
|
|
|
2. Креслимо у масштабі поперечний переріз, розташовуючи його у першій чверті допоміжних осей х1 та у1, і зазначаємо координати центрів ваги простих поперечних перерізів (рис. 2.9). Показуємо особисті осі х0 у0 простих перерізів, відносно яких відомі осьові моменти інерції.
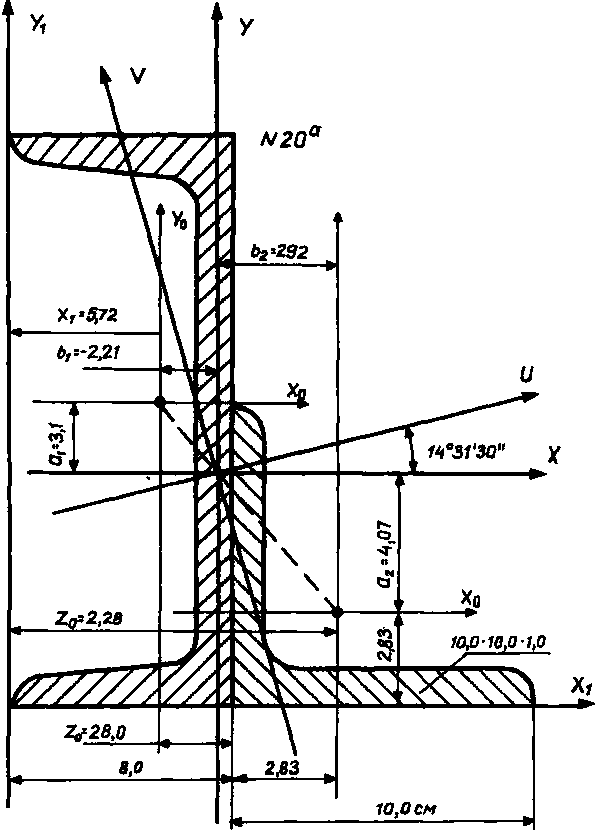
Рис. 2.9. Креслення перерізу
3. Визначаємо координати центра ваги складного поперечного перерізу в допоміжних осях х1 і у1, використовуючи формулу (2.3):
![]() ;
;
![]() .
.
За одержаними даними наносимо точку О (центр ваги складного поперечного перерізу) і проводимо центральні осі х та у паралельно допоміжним осям х1 і у1 . Точка О повинна лежати на лінії, що з’єднує центри ваги швелера та кутника.
4. Визначаємо центральні моменти інерції складного поперечного перерізу відносно осей х та у, використовуючи формулу переходу до паралельних осей (2.12):
![]()
![]() ;
;
![]()
![]() .
.
5. Визначаємо відцентровий момент інерції складного поперечного перерізу відносно осей х та у, використовуючи формулу переходу до паралельних осей (2.11):
![]() ,
,
де
![]() - відцентровий момент інерції швелера
відносно головних центральних осей
швелера, який, як відомо, дорівнює
нулю;
- відцентровий момент інерції швелера
відносно головних центральних осей
швелера, який, як відомо, дорівнює
нулю;
![]() -
відцентровий момент інерції рівнополичного
кутника
відносно його центральних осей не
дорівнює нулю, а вираховується по формулі
(2.15), знак якого визначається із рис.
2.6. Тоді:
-
відцентровий момент інерції рівнополичного
кутника
відносно його центральних осей не
дорівнює нулю, а вираховується по формулі
(2.15), знак якого визначається із рис.
2.6. Тоді:
![]() .
.
Відцентровий момент інерції усього складного поперечного перерізу відносно осей х і у буде дорівнювати:
![]()
6. Визначаємо кут нахилу головних центральних осей u та v складного поперечного перерізу до центральних х і у:
![]() ;
;
![]() ,
,
![]() .
.
Відкладаємо цей кут проти годинникової стрілки і проводимо головні центральні осі u та v.
7. Визначаємо
головні центральні моменти інерції за
формулами переходу до повернутих осей
(2.13). Якщо α = 14°З1’30";
![]() =
0,25; соsα
=
0,97; sin2α
= 0,472. Тоді:
=
0,25; соsα
=
0,97; sin2α
= 0,472. Тоді:
![]()
![]()
![]()
Правильність
визначених моментів інерції контролюємо
за формулою (2.14): ![]() ;
;
![]() ;
;
![]() .
.
Погрішність не повинна бути більшою 5%.

![]() ;
;
![]() .
.
![]() = 3,32 см.
= 3,32 см.

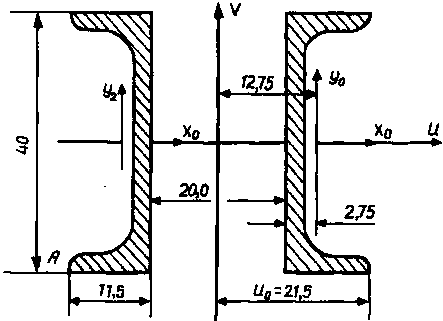 Рис.
2.7. Креслення перерізу
Рис.
2.7. Креслення перерізу