
- •5. Стійкість стиснутих стержнів
- •5.1. Формула Ейлера для визначення критичної сили стиснутого стержня
- •5.2. Розрахунки на стійкість стержнів
- •5.3. Перевірний розрахунок стиснутих стержнів
- •5.4. Проектний розрахунок стиснутих стержнів
- •5.5. Завдання для виконання розрахункової роботи
- •Питання для самоконтролю
5. Стійкість стиснутих стержнів
5.1. Формула Ейлера для визначення критичної сили стиснутого стержня
Виконуючи розрахунки на міцність та жорсткість при різних деформаціях, ми вважали, що під час деформації будь-якої системи має місце лише одна наперед відома форма рівноваги. Насправді ж у деформованому стані рівновага між зовнішніми силами пружності може бути не тільки стійкою, а й нестійкою.
Пружна рівновага буде стійкою, якщо деформоване тіло при будь-якому малому відхиленні від стану рівноваги намагається повернутися до початкового стану й повертається до нього після припинення зовнішнього впливу, який порушив початковий стан рівноваги (рис. 5.1, а).
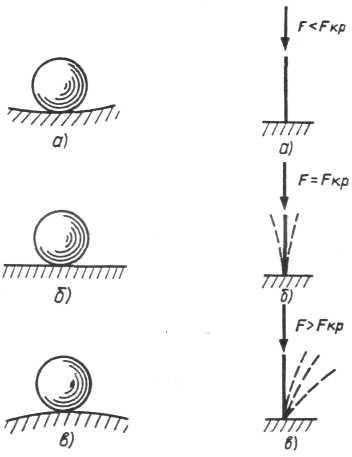
Рис. 5.1. Стан рівноваги стержня
Пружна рівновага нестійка, якщо деформоване тіло, виведене з неї будь-якою зовнішньою дією, продовжує деформуватися в напрямі наданого йому відхилення і після припинення зовнішньої дії у вихідний стан не повертається (рис. 5.1, в). Між цими двома станами рівноваги існує перехідний стан, який зветься критичним, при якому деформоване тіло перебуває у байдужій рівновазі: воно може зберегти вихідну форму, але може й втратити її внаслідок самого незначного впливу (рис. 5.1, б).
Стійкість форми рівноваги деформованого тіла залежить від прикладених до нього навантажень. Наприклад, якщо сили, що стискають стержень, невеликі, то вихідна форма рівноваги залишається стійкою (рис. 5.1, а). При зростанні прикладених сил досягається стан байдужої рівноваги, при якому поряд з прямолінійною формою стержня можливі суміжні з нею злегка викривлені форми рівноваги (штрихові лінії на рис. 5.1, б). При дальшому найнезначнішому збільшенні навантаження характер деформації стержня різко змінюється - стержень випучується (рис. 5.1, в), прямолінійна форма рівноваги перестає бути стійкою. Це означає, що навантаження перевищило критичне значення.
Навантаження, перевищення якого спричинює втрату стійкості вихідної форми тіла, зветься критичним і позначається Ркр.
При розрахунку на стійкість критичне навантаження подібне руйнівному при розрахунку на міцність. Для забезпечення певного запасу стійкості необхідно, щоб задовольнялася умова:
![]() .
(5.1)
.
(5.1)
Тут ![]() ,(5.2)
,(5.2)
де Р - діюче навантаження;
nст - коефіцієнт запасу стійкості.
Отже, щоб розрахувати стиснуті стержні на стійкість, треба вивчити способи визначення критичних навантажень Ркр.
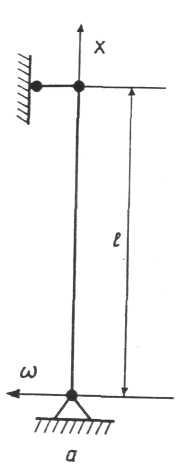
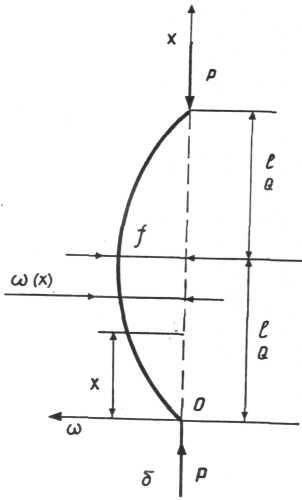
Рис. 5.2. Розрахункова схема стержня
З усієї різноманітності розрахунків на стійкість пружних систем, розглянемо лише приклад втрати стійкості при стисканні довгого тонкого стержня, або так зване поздовжнє згинання. Припустимо, що під дією сили Р, яка дещо перевищує критичну силу Ркр, стержень з шарнірно закріпленими кінцями (рис. 5.2, а) трохи зігнувся (рис. 5.2, б). Віднесемо викривлену вісь стержня до прямокутної системи координат, вибравши початок координат у точці 0.
Припустимо, що критична сила Ркр не спричинює в стержні напруження, які перевищують границю пропорційності, і що розглядаються лише малі відхилення від прямолінійної форми. Тоді для визначення поздовжньої сили можна скористатися приближеним диференціальним рівнянням пружної лінії:
![]() (5.3)
(5.3)
Тут Imin - найменший момент інерції перерізу стрижня.
В даному випадку ураховується найменша жорсткість стержня ІЕmin, оскільки, очевидно, прогин відбудеться перпендикулярно до осі найменшої жорсткості.
На відміну від поперечного згинання при поздовжньому в правій частині цього рівняння слід ставити знак «мінус», оскільки абсолютне значення згинального моменту:
![]() ,
(5.4)
,
(5.4)
а
знак прогину завжди протилежний знаку
другої похідної, тобто знаки моменту
М(х)
та другої похідної
![]() протилежні при
будь-якому
напрямі осі ω.
протилежні при
будь-якому
напрямі осі ω.
Підставивши
в рівняння (5.3) вираз (5.4) для згинального
моменту
дістанемо: ![]() . (5.5)
. (5.5)
Або ![]() .
(5.6)
.
(5.6)
Ввівши
позначення: ![]() ,
(5.7)
,
(5.7)
перепишемо рівняння (5.7) у вигляді:
![]() .
(5.8)
.
(5.8)
Ми дістали однорідне лінійне диференціальне рівняння, загальний інтеграл якого, як відомо, можна виразити функцією:
![]() .
(5.9)
.
(5.9)
Сталі інтегрування А та В повинні добиратися так, щоб задовольнялися граничні умови:
при х = 0, ω(х) = 0; при х = l, ω(х) = 0.
З першої граничної умови випливає, що В = 0, тобто:
![]() .
(5.10)
.
(5.10)
Із другої умови знайдемо:
![]() .
(5.11)
.
(5.11)
Якщо
припустити, що А
=
0, то прогин буде тотожно дорівнювати
нулю, тобто: ![]() .
.
Цей
розв’язок відповідає одній з можливих
форм рівноваги стиснутого стержня, а
саме – стержня прямолінійній формі.
Нас же цікавить значення сили Р,
при
якому стає можливою друга форма рівноваги
- криволінійна. Оскільки А ≠
0,
то при викривленій формі стрижня повинна
виконуватися рівність![]() .
.
Корінь
цього рівняння kl
може
мати нескінченну кількість значень: 0;
π; 2 π; ... , тобто: ![]() ,
,
де п - довільне ціле число.
Однак перший корінь kl = 0 відкидається, оскільки він не відповідає вихідним даним задачі. Отже:
![]() .
(5.12)
.
(5.12)
Тоді
з рівняння (5.7) дістанемо вираз для сили
![]() :
:
![]() .
(5.13)
.
(5.13)
Рівняння (5.13) є формулою, що вперше була виведена Ейлером.
Практично нас цікавить найменше значення поздовжньої сили стиску, при якому стає можливим поздовжнє згинання. Найменше значення критичної сили Ркр дістанемо при п = 1 та kl = π:
![]() .
(5.14)
.
(5.14)
В даному випадку при п = 1, максимальний прогин ω має місце посередині стержня, при х = l/2 (рис. 5.2, б).
Ми розглянули так званий основний випадок навантажування й закріплення кінців стиснутого стержня - стержня з шарнірно обпертими кінцями.
Якщо стержень закріплений інакше Ркр знаходиться по формулі:
![]() .
(5.15)
.
(5.15)
|
На рисунку 5.3 показані інші види закріплення та значення коефіцієнтів μ. З формули Ейлера (5.15) видно, що критичне навантаження залежить від найменшої жорсткості ЕImin, довжини стрижня l та коефіцієнта μ. Виведення формули Ейлера ґрунтується на застосуванні диференціального рівняння пружної лінії. Тому скористатися цією формулою можна лише тоді, коли справедливий закон Гука, тобто доки критичне напруження (напруження стискання, що відповідає критичній силі) не |
Р |
перевищує границі пропорційності:
![]() .
(5.16)
.
(5.16)
Виведемо формулу для критичного напруження:
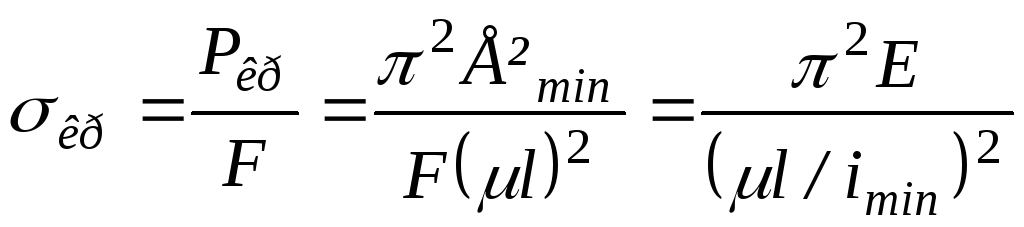 ,
(5.17)
,
(5.17)
де
![]() - найменший з головних радіусів інерції
стержня.
- найменший з головних радіусів інерції
стержня.
Ввівши безрозмірну величину:
![]() ,
(5.18)
,
(5.18)
що називається гнучкістю стержня, остаточно маємо:
![]() ,
(5.19)
,
(5.19)
тобто критичне напруження стержня залежить тільки від пружних властивостей матеріалу (модуля пружності Е) та гнучкості стержня λ.
Однак
з умови (5.16) застосовності формули Ейлера
відповідно до формули (5.19) маємо: ![]() .
.
Тому: ![]() .
(5.20)
.
(5.20)
Це означає, що формула Ейлера стає непридатною при гнучкості стержня, меншій за граничне значення λ, яке залежить тільки від властивостей матеріалу.
Наприклад, для сталі Ст3 σпц = 200 МПа, Е= 2× 105 МПа, тоді:
![]() .
.
Для деревини, наприклад, сосни λ ≈ 100. Для чавуну λ ≈ 80.
Використання формули Ейлера для стержнів, що втрачають стійкість за границею пружності, не можливо.
Тому Ф. С. Ясинський зібрав та обробив великий дослідний матеріал щодо поздовжнього згинання стержнів, у результаті чого склав таблицю критичних напружень залежно від гнучкості для низки матеріалів та запропонував просту емпіричну формулу для обчислення критичних напружень за границею пропорційності:
![]() .
(5.21)
.
(5.21)
Значення коефіцієнтів а та b для матеріалів береться з таблиць.
Наприклад, для сталі Ст2, Ст3 а = 310 МПа, b= 1,14 МПа; для чавуна а = 776 МПа, b = 12,0 МПа.
Формулою Ясинського можна користуватись при 40 < λ < 100 для сталі.
При λ0 < 40 стержні рахуються на міцність як при простому розтягу або стиску. Ці стержні на поздовжній згин не працюють.
Стержні, в яких λ <λ0 називають стержнями малої гнучкості.

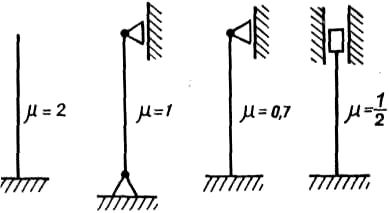 ис.
5.3. Види закріплень кінців стержня
ис.
5.3. Види закріплень кінців стержня