
- •З м і с т
- •Розділ 1 застосування диференціального числення для дослідження функцій
- •1.1. Зростання і спадання функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.2. Локальний екстремум функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.3. Опуклість і угнутість кривих. Точки перегину
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.4. Асимптоти кривих
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.5. Схема дослідження функції та побудова її графіка
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 2
- •2.1. Означення та область визначення. Частинні похідні першого порядку
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.2. Повний диференціал функції. Похідні складених функцій
- •(2.6) Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.3. Частинні похідні вищих порядків. Похідні неявно заданих функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.4. Рівняння дотичної площини і нормалі до поверхні. Екстремум функції двох змінних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 3 невизначений інтеграл
- •3.1. Поняття первісної функції та невизначеного інтеграла. Метод безпосереднього інтегрування
- •Таблиця основних інтегралів
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Зразки розв’язування задач
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.5. Інтегрування функцій, раціонально залежних від тригонометричних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.6. Інтегрування деяких іраціональних функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Вища математика
Зразки розв’язування задач
Обчислити інтеграли.
1.
![]() .
.
Дріб
![]() є правильним. Розкладемо його на суму
найпростіших дробів. Коренями
знаменника є дійсні числа
є правильним. Розкладемо його на суму
найпростіших дробів. Коренями
знаменника є дійсні числа![]() та
та![]() ,
серед яких немає кратних. Тому чисельниками
кожного дробу будуть числа
,
серед яких немає кратних. Тому чисельниками
кожного дробу будуть числа![]() .
Отримаємо:
.
Отримаємо:![]() .
Помноживши обидві частини рівності на
спільний знаменник, здобудемо:
.
Помноживши обидві частини рівності на
спільний знаменник, здобудемо:
![]() ,
або
,
або
![]() .
.
![]() Порівнюючи
коефіцієнти при однакових степенях
Порівнюючи
коефіцієнти при однакових степенях
![]() в правій і лівій частинах, отримаємо
систему рівнянь:
в правій і лівій частинах, отримаємо
систему рівнянь:
![]()
 з якої знайдемо
з якої знайдемо![]() .
.
Отже, розкладання раціонального дробу на найпростіші має вигляд:
![]() .
.
Невідомі
![]() і
і![]() можна визначити інакше. Після того, як
позбулися знаменника, змінній
можна визначити інакше. Після того, як
позбулися знаменника, змінній![]() можна надати стільки часткових значень,
скільки коефіцієнтів треба визначити
(в даному випадку – два значення).
Особливо зручно надавати
можна надати стільки часткових значень,
скільки коефіцієнтів треба визначити
(в даному випадку – два значення).
Особливо зручно надавати![]() ті значення, які є дійсними коренями
знаменника. Застосуємо цей прийом до
нашого дробу. Після звільнення від
знаменника отримали вираз
ті значення, які є дійсними коренями
знаменника. Застосуємо цей прийом до
нашого дробу. Після звільнення від
знаменника отримали вираз![]() .
.
 При
При
![]() :
:![]() ,
звідки
,
звідки![]()
![]() .
.
При
![]() :
: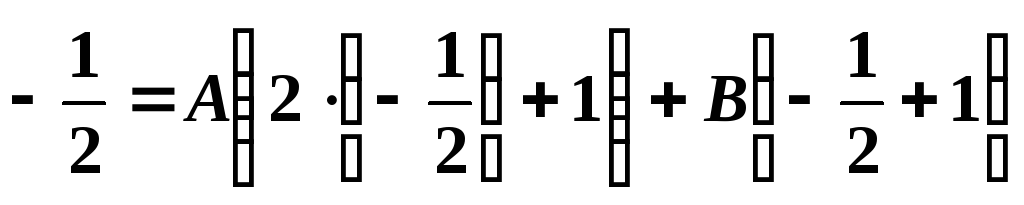 ,
звідки
,
звідки
![]() ,
,
![]() .
.
В
результаті отримали ті самі значення
![]() і
і![]() ,
що й при першому способі визначення
коефіцієнтів.
,
що й при першому способі визначення
коефіцієнтів.
Таким чином,

Зауваження. Якщо корені знаменника – числа тільки дійсні та різні, спосіб часткових значень є найзручнішим. В інших випадках поєднують обидва способи.
2.
![]() .
.
Розкладемо
знаменник дробу на множники:
![]() .
Коренями тричлена
.
Коренями тричлена![]() є числа
є числа![]() та
та![]() .
Тому
.
Тому![]() .
Отже
.
Отже![]() .
Розкладемо даний дріб на суму найпростіших:
.
Розкладемо даний дріб на суму найпростіших:
![]() .
.
Тоді
![]() .
.
Для
визначення коефіцієнтів
![]() застосуємо часткові значення
застосуємо часткові значення![]() .
.
 При
При
![]() :
:![]() ,
,
при
![]() :
:![]() ,
,
при
![]() :
:![]() .
.
Отже,

Шуканий інтеграл:
![]()

3.
 .
.
Підінтегральний дріб є неправильним, тому необхідно виділити цілу частину, поділивши чисельник на знаменник:
![]()
![]()

![]()
-
![]()
![]()
_________________
![]()
![]()
![]()
-
![]()
![]()
_______________
![]()
![]()
![]()
-
![]()
![]()
______________
![]()
![]()
![]()
-
![]()
![]()
_____________
![]()
![]()
Отже,

![]() .
.
Дріб
![]() вже є правильним, розкладемо його на
суму найпростіших:
вже є правильним, розкладемо його на
суму найпростіших:
![]() ,
,
![]() .
.
 При
При
![]() :
:![]() ,
,
при
![]() :
:![]() .
.

Шуканий
інтеграл дорівнюватиме:

Зауважимо,
що інтеграл
![]() може бути обчислений іншими способами,
наприклад, зведенням до суми двох
інтегралів, один з яких – табличний, а
в другому треба застосувати заміну
змінної.
може бути обчислений іншими способами,
наприклад, зведенням до суми двох
інтегралів, один з яких – табличний, а
в другому треба застосувати заміну
змінної.
4. .
.
Як і в попередньому прикладі підінтегральний дріб є неправильним, тому виділивши в ньому цілу частину, отримаємо:
 .
.
Тепер даний інтеграл можна подати у вигляді суми двох інтегралів:

![]()
Щоб
обчислити другий інтеграл, розкладемо
дріб
![]() на суму найпростіших дробів.
на суму найпростіших дробів.
 ,
,
![]() .
.
Для
отримання коефіцієнтів
![]() і
і![]() використаємо корінь
використаємо корінь![]() знаменника. При
знаменника. При![]()
![]()
![]() .
Зважаючи на те, що інших коренів не
існує, для визначення
.
Зважаючи на те, що інших коренів не
існує, для визначення![]() порівняємо коефіцієнти при
порівняємо коефіцієнти при![]() в обох частинах рівності. В лівій
частині він дорівнює
в обох частинах рівності. В лівій
частині він дорівнює![]() ,
а в правій
,
а в правій![]() .
Отже,
.
Отже,![]()
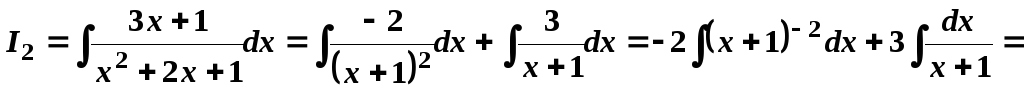
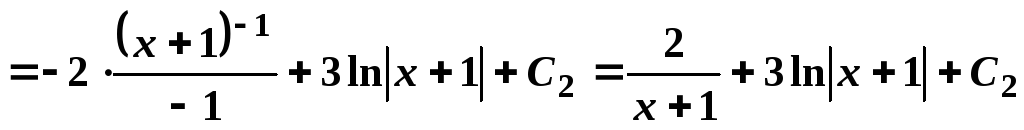 .
.
Шуканий
інтеграл дорівнюватиме:
 .
.
5.
![]() .
.
Дріб
![]() є правильним. Розкладемо знаменник
дробу на множники:
є правильним. Розкладемо знаменник
дробу на множники:![]() .
Бачимо, що знаменник має один дійсний
корінь
.
Бачимо, що знаменник має один дійсний
корінь![]() та пару спряжених коренів
та пару спряжених коренів![]() .
Тому розкладання дробу на суму
найпростіших має вигляд:
.
Тому розкладання дробу на суму
найпростіших має вигляд:
 ,
звідки
,
звідки
![]() .
.
 При
При
![]() :
:![]() ,
,
при
![]() :
:![]() ,
,
при
![]() :
:![]() .
.
Отже,
![]() .
.
Перший
інтеграл є табличним
![]() .
Для інтегрування другого доданку
розіб’ємо дріб на суму двох дробів:
.
Для інтегрування другого доданку
розіб’ємо дріб на суму двох дробів:![]() . Перший з них інтегруємо, використовуючи
заміну змінної:
. Перший з них інтегруємо, використовуючи
заміну змінної:
 .
.
Другий
інтеграл дорівнюватиме:
![]() .
.
Таким
чином,
![]() .
.
6.
![]() .
.
Знаменник дробу не має дійсних коренів, тому не розкладається на лінійні множники. Вчинемо інакше, а саме виділимо в ньому повний квадрат.
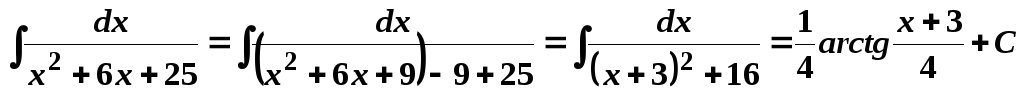 .
.
7.
![]() .
.
Так
само, як в попередньому прикладі,
знаменник не розкладається на множники.
Перетворимо дріб під інтегралом:
виділимо в чисельнику від
![]() похідну знаменника, яка дорівнює
похідну знаменника, яка дорівнює![]() .
.
![]() .
.
Отримаємо:
 .
.
До першого інтегралу застосуємо метод заміни змінної, до другого – виділення повного квадрату. Будемо мати:

(вираз
не містить модуля, бо
![]() >
>![]() ).
).
 .
.
Тоді
![]() .
.
8.
 .
.
Знаменник
дробу
![]() має кратні комплексні корені, тому
має кратні комплексні корені, тому
 .
.
![]()
![]() .
.
Порівняємо
коефіцієнти при однакових степенях
![]() :
:
 при
при
![]() :
:![]() ,
,
при
![]() :
:![]() ,
,
при
![]() :
:![]() ,
,
при
![]() :
:![]() .
.
Будемо мати:
 .
.
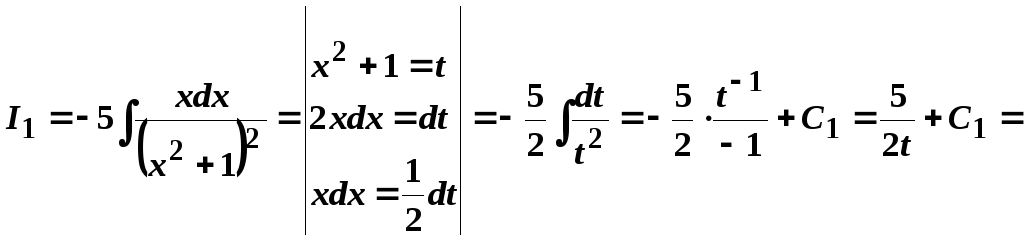
 .
.

![]() .
.
Отже,
 .
.
