5.2. Элементарные логические функции и функциональная полнота систем логических функций

Логические функции, соответствующие логическим операциям В²aВ, называют элементарными. Количество логических функций отnпеременных определяется выражением 2²ⁿ, поскольку|Bⁿ|=2ⁿ, а на каждом из2ⁿнаборов логическая функция может принимать одно из значений из того же множества В (табл.5.4).

Табл.5.4

№	Набор	Номер логической функции
п/п	значений переменных	0	1	2	3	...	22n-1
1	00...00	0	1	0	1	...	1
2	00...01	0	0	1	1	...	1
3	00...10	0	0	0	0	...	1
4	00...11	0	0	0	0	...	1
. . .	. . .	. . .	. . .	. . .	. . .	...	. . .
22	11...11	0	0	0	0		1

Например, рассмотрим все логические функции одной переменной (табл.5.5).

Табл.5.5

	Логическая функция
х	f0(x)	f1(x)	f2(x)	f3(x)
0	0	1	0	1
1	0	0	1	1

Поскольку 2²¹=4, то имеется четыре логических функции одной переменной, две из них - константы:f₀(x)=0,f₃(x)=1.f₀(x)- константа нуля,f₃(x)- константа единицы. Здесь номер функции означает десятичное число, соответствующее двоичному числу, записанному в первом и последнем столбцах табл.5.5.

Функция f₁(x)=х, т.е. совпадает со значением переменной. Эта функция называется функцией повторения. Функцияf₂(x)=нам уже известна - это инверсия.

Можно заметить, что для каждой функции одной переменной существует инверсная ей:

f₀(x)=₃(х)==1;

f₃(x)=₀(х)==0;

f₁(x)=₂(х)==х;

f₂(x)=₁(х)=.

Рассмотрим все функции двух переменных (табл.5.6).

Табл.5.6

Вес разряда вектора значения функции

		20	21	22	23
		Набор				Название		Формула
20	х1	0	1	0	1		функции	(Вебба)
21	х2	0	0	1	1
	f0	0	0	0	0		Константа 0	0
	f1	1	0	0	0		Функция Пирса (Вебба), "стрелка Пирса", ИЛИ-НЕ	х1¯х2=
	f2	0	1	0	0		Запрет х2	х1
	f3	1	1	0	0		Отрицание х2
	f4	0	0	1	0		Запрет х1	х2
	f5	1	0	1	0		Отрицание х1
	f6	0	1	1	0		Сложение по mod2	х1Åх2= х1Úх2
	f7	1	1	1	0		Функция Шеффера, "штрих Шеффера", И-НЕ	х1|х2= 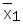Ú
	f8	0	0	0	1		Конъюнкция, И	х1х2
	f9	1	0	0	1		Эквиваленция (эквивалентность)	х1«х2= х1х2Ú
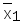
	f10	0	1	0	1		Повторение х1	х1
	f11	1	1	0	1		Импликация х2в х1	х2®х1 Úх1
	f12	0	0	1	1		Повторение х2	х2
	f13	1	0	1	1		Импликация х1в х2	х1®х2 Úх2
	f14	0	1	1	1		Дизъюнкция, ИЛИ	х1Úх2
	f15	1	1	1	1		Константа 1	f1

Всего таких функций имеется 2²²=2⁴=16. Согласно табл.5.6 существуют две функции - константы 0,1, которые не зависят от значения переменных. Есть функции, зависящие только от одной переменной. Такие функции называют вырожденными. Перечислим их:

f₀(x₁x₂)=0; f₅(x₁x₂)=;f₃(x₁x₂)=;

f₁₅(x₁x₂)=1;f₁₀(x₁x₂)=х₁;f₁₂(x₁x₂)=х₂.

Некоторые функции мы тоже уже знаем: конъюнкцию f₈(x₁x₂)=х₁х₂(точку между х₁и х₂опускаем); дизъюнкциюf₁₄(x₁x₂)=х₁Úх₂; эквиваленцию (эквивалентность)f₉(x₁x₂)=х₁«х₂=х₁х₂Ú(здесь эквиваленция представлена в виде дизъюнкции двух конъюнкций, что можно доказать, составив таблицу истинности); импликациюf₁₃(x₁x₂)=х₁®х₂=Úх₂; импликациюf₁₁(x₁x₂)=х₂®х₁=Úх₁.

Кроме этого, имеются другие функции, зависящие от двух переменных: f₁(x₁x₂)=носит название функции Пирса (Вебба) ("стрелка Пирса"),f₇(x₁x₂)=Úносит название функции Шеффера ("штрих Шеффера"),f₂(x₁x₂)=х₁называется запретом х₂, аf₄(x₁x₂)=х_2­- запретом х₁. Функцияf₆(x₁x₂)называется сложением по модулю два, это функция, инверсная эквиваленции и обозначается х₁Åх₂(mod2).

Элементарные логические функции позволяют получить сложные функции от большего числа аргументов путем подстановки в данную функцию вместо ее переменных других функций. Такой метод получения функций называется суперпозицией. Например, имея элементарные функции двух переменных z₁=x₁x₂ иz₂=x₃Úx₄можно получить функцииz₃=х₁(x₃Úx₄),z₄=x₃Úх₁x₂, зависящие от трех переменных.

При использовании суперпозиции возникает следующая проблема: каким должен быть минимальный состав элементарных логических функций, который позволяет путем их суперпозиции получить любую сколь угодно сложную логическую функцию от конечного числа переменных.

Эта проблема называется проблемой функциональной полноты логических функций. Для ее решения были выделены следующие классы логических функций:

1) Класс функций, сохраняющих константу 0. В этот класс входят функции, которые на нулевом наборе переменных принимают нулевое значение: f(00...0)=0. Такова, например, конъюнкцияf₈=х₁х₂f₈(00)=0×0=0.

2) Класс функций, сохраняющих константу 1. В этот класс входят функции, которые на единичном наборе переменных принимают единичное значение: f(11...1)=1. Этим свойством также обладает конъюнкцияf₈(11)=1×1=1. Классы 1,2 легко устанавливаются по таблице истинности.

3) Класс самодвойственных функций. Логические функции f(х₁х₂...х_n) иg(х₁х₂...х_n) называются двойственными, если имеет место равенство

f(х₁х₂...х_n)=,

т.е. если одна функция получается из другой, если провести замену всех переменных на их инверсии и провести инверсию функции.

Например, f₈(х₁х₂)=х₁х₂иf₁₄(x₁x₂)=х₁Úх₂двойственны:

.

Это можно доказать, построив таблицу истинности:

Табл.5.7

х1	х2		х1х2
0	0	0	0
0	1	0	0
1	0	0	0
1	1	1	1

Логическая функция называется самодвойственной, если она двойственна по отношению к самой себе:

f(х₁х₂...х_n)=.

Такова, например, функция f₁₀(x₁x₂)=x₁:

.

Самодвойственность устанавливается по таблице истинности следующим образом: значения функции, симметричные относительно середины таблицы инверсны. Например, дляf₁₀(x₁x₂)значения функции представляют собой вектор 01 01, каждый разряд которого является инверсным по отношению к симметричному разряду относительно середины, отмеченной пунктиром. Эти разряды соответствуют инверсным наборам х₁х₂: 00 - 11, 01 - 10. Самодвойственны функции,,х₂,х₁.

4) Класс линейных функций. Логическая функция называется линейной, если возможно представление в виде линейного полинома, использующего функцию сложения по модулю 2 (mod2):

f(x₁x₂)=с₀Åс₁х₁Åс₂х₂,

где с₀,с₁,с₂- константы 0,1.

Например, для сложения по модулю 2(mod2):

f₆(x₁x₂)=х₁Åх₂.

с₀=0, с₁=с₂=1:

f₆(x₁x₂)=0Å1×х₁Å1х₂.

Получим все линейные функции двух переменных, задав все возможные значения с₀с₁с₂(табл.5.8).

Табл.5.8

с0	с1	с2	Вид полинома
0	0	0	0	Можно доказать,
0	0	1	х2	используя, например,
0	1	0	х1	таблицу истинности,
0	1	1	х1Åх2	что:
1	0	0	1
1	0	1	1Åх2	=
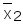
1	1	0	1Åх1	=
1	1	1	1Åх1Åх2	=

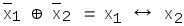
Видно, что каждая линейная функция имеет инверсную ей. Таким образом, линейные функции - константа 0, константа 1, повторение х₁,х₂, инверсии:,, сложение по модулю 2 (х₁Åх₂) и инверсная ей эквиваленция.

5) Класс монотонных функций. Монотонная функция на большем сравнимом наборе переменных принимает не меньшие значения. Это удобно проверять на решетках Хассэ. Так, для двух переменных решетка имеет вид рис.5.1.

На рис.5.1 видно, что 11>01>00, 11>10>00(частично упорядоченное множество наборов).

Рис.5.1. Решетка Хассэ для двух переменных

с указанием значений f₁₀(х₁х₂)=х₁

Очевидно, что константы 0,1 - монотонные функции, дизъюнкция, и конъюнкция - монотонные функции, повторения х₁,х₂- монотонные функции. На рис.5.1 проставлены значения монотонной функции х₁.

Система логических функций называется функционально полной, если любая произвольная логическая функция от любого числа переменных может быть представлена в виде суперпозиции логических функций из этой системы.

Функционально полная система логических функций называется минимальной, если удаление из нее хотя бы одной функции превращает ее в неполную. Критерий функциональной полноты логических функций устанавливает теорема Поста-Яблонского, в которой утверждается, что для функциональной полноты систем логических функций необходимо и достаточно, чтобы они содержали следующие функции:

- не сохраняющую константу 0;

- не сохраняющую константу 1;

- несамодвойственную;

- нелинейную;

- немонотонную.

Функционально полные системы логических функций представляют собой базис. Всего можно получить 17 различных минимальных базисов из логических функций двух переменных.

Оказывается, имеются функции, обладающие всеми пятью отмеченными свойствами. Таковы функции f₁(x₁x₂)=иf₇(x₁x₂)=Ú. Часто их называют соответственно ИЛИ-НЕ, И-НЕ. Таким образом, это базисы, состоящие из одной функции (базис Вебба и базис Шеффера). Этот факт очень важен при технической реализации дискретных устройств: достаточно иметь элементы, реализующие только одну из этих функций, чтобы построить любую, сколь угодно сложную схему. Более подробно этот вопрос будет рассмотрен при изучении синтеза автоматов.

Имеются базисы, состоящие из двух функций:

Иногда используется не минимальный базис - из трех функций:

Имеется и довольно экзотический базис Жегалкина:

В дальнейшем нам пригодится так называемый импликативный базис

Если рассматривать логические функции большего числа аргументов, то можно поставить задачу отыскания базисов, не зависящих от их некоторых модификаций соответствующих функций. Такие модификации могут быть, например, вызваны подстановкой констант 0,1 и инверсией переменных, что происходит при некоторых отказах соответствующих логических элементов. Такие базисы называют толерантными. Например, логическая функция четырех переменных - толерантный базис - функционально полная толерантная функция, которая при подстановке констант вместо переменных или при инверсии переменных модифицируется также в базисную функцию: