3.3. Изоморфизм графов

Как мы убедились, граф может быть задан различными способами. Он может быть изображен на чертеже, задан матрицей инцидентности, списком ребер или матрицей смежности, фактор-множеством и т.д. Вид чертежа зависит от формы линий и взаимного расположения вершин. Иногда не так легко понять, одинаково ли графы, изображенные разными чертежами. Вид матриц и списка ребер зависит от нумерации вершин и ребер графа. Строго говоря, граф считается полностью заданным, если нумерация его вершин зафиксирована; графы, отличающиеся только нумерацией вершин, называются изоморфными.

Например, графы, изображенные на рис.3.9, изоморфны.

Рис.3.9. Изоморфные графы а) и б), отличающиеся

только перенумерацией вершин 51, 15

Если граф ориентированный, то направление дуг в изоморфных графах должно совпадать.

Чтобы узнать, представляют ли две матрицы смежности изоморфные графы, можно произвести всевозможные одинаковые перестановки строк и столбцов.

Если после одной из этих перестановок возникнет матрица, совпадающая с заданной, то сравниваемые графы изоморфны. Для этого требуется максимум n! перестановок, гдеn- число вершин графа.

Иногда для определения изоморфности определяют параметры обоих графов: число вершин, число ребер, число компонент связности, последовательность степеней вершин в убывающем порядке.

Если какие-то из этих параметров различны, то эти графы различны. Однако если все параметры у двух графов совпали, это не гарантирует изоморфности.

Так, на рис.3.10 приведены два графа, у которых эти параметры совпадают, и ,тем не менее, они различны.

Рис.3.10. Пример неизоморфных графов а) и б)

На рис.3.11 приведен граф, изоморфный графу "пятиконечная звезда" (рис.3.1).

Рис.3.11. Граф, изоморфный графу

"пятиконечная звезда"

3.4. Понятие о задачах на графах

О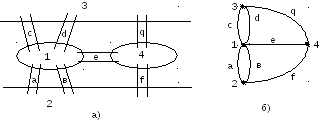дной из первых задач в теории графов считается задача Эйлера (1736 г.) - задача о кенигсбергских мостах. Ее решение Эйлер опубликовал, когда работал в Российской Академии наук. Расположение мостов в г.Кенигсберге на реке Перголь в то время приведено на рис.3.12а, а соответствующий неориентированный граф - на рис.3.12б. Требуется пройти каждый мост по одному разу и вернуться в исходную часть города.

Рис.3.12. Задача о кенигсбергских мостах

Обходу мостов соответствует последовательность ребер графа, в которой два соседних ребра имеют общую вершину. Так как в конце обхода нужно вернуться в исходную часть города и на каждом мосту побывать по одному разу, такой обход должен быть простым циклом, содержащим все ребра графа. В дальнейшем такие циклы стали называть эйлеровыми, а графы, имеющие эйлеровые циклы - эйлеровыми графами.

Эйлеров цикл можно вычертить, не отрывая пера от бумаги, причем процесс вычерчивания начинается и заканчивается в одной точке.

Таков граф "звезда", изображенный на рис.3.1.

Оказывается, конечный неориентированный граф Gэйлеров тогда и только тогда, когда он связен и степени всех его вершин четны.

В графе, соответствующем задаче о кенигсбергских мостах, все вершины нечетны. Следовательно, эта задача неразрешима.

С другой задачей - задачей раскраски графов связана так называемая "задача четырех цветов". Это задача раскраски карты, т.е. разбиения плоскости на связные области. Достаточно ли четырех цветов для раскраски любой карты? По некоторым сведениям, еще в 1840 г. об этой задаче знал известный немецкий математик Мебиус. Только сравнительно недавно два американских математика доказали разрешимость этой задачи, использовав компьютер.

В практических приложениях имеет большое значение задача нахождения кратчайшего пути между двумя вершинами связного неориентированного графа. К такой задаче сводятся многие задачи выбора наиболее экономичного (с точки зрения расстояния или времени (числа шагов) или стоимости энергозатрат, трудоемкости) маршрута по имеющейся карте дорог, многие задачи выбора наиболее экономичного способа перевода системы из одного состояния в другое и т.д.

Имеется транспортная задача, решение которой определяет рациональный план перевозок, который обеспечивает, например, их минимальную стоимость или доставку в кратчайшее время.

Другая задача - о наибольшем потоке в частном классе графов - транспортной сети - формулируется следующим образом. При заданной конфигурации транспортной сети и известной пропускной способности ее дуг найти наибольшее значение потока, который может пропустить сеть, а также распределение этого потока по дугам транспортной сети.

Графы используются при анализе и синтезе систем с конечным числом состояний. Вершины графа в этом случае соответствуют состояниям дискретной системы, а дуги, например, условиям перехода между состояниями или вероятностям перехода между ними. Часто также используются граф-схемы алгоритмов, о которых будет речь идти в дальнейшем.

Графом можно описать схемы технических устройств, например, линии связей печатной платы, топопологию микросхем т.д.

Рассмотрим пример представления графом изменения состояний дискретной системы.

Это так называемая задача о ханойской башне. Имеется три стержня, на первом из которых нанизаны nдисков, диаметр который убывает снизу вверх. Ставится цель: перекладывая диски по одному, расположить их в таком же порядке на третьем стержне, используя в качестве промежуточного второй стержень и соблюдая условия, чтобы ни на каком месте больший диск не оказался выше меньшего ни на одном из стержней. Оптимизация заключается в достижении цели за наименьшее число шагов.

Рассмотрим n=1 (рис.3.13).

Рис.3.13. Задача о ханойской башне для n=1

Задача для n=1 решается за один шаг, но возможен и неоптимальный вариант - два шага, т.е. сначала диск устанавливают на второй стержень, а потом на третий.

Обозначим X, Y и Zмножества дисков, надетых соответственно на первый, второй и третий стержни. Состояние такой системы будем описывать набором элементов этих множеств (X,Y,Z).

Тогда возможные состояния такой системы имеют вид:

XYZ

(1,0,0) - исходное,

(0,0,1) - целевое,

(0,1,0) - промежуточное.

Представим состояния системы в виде графа с использованием координатной плоскости с осями XиZ(рис.3.14).

Рис.3.14. Представление графом задачи

о ханойской башне при n=1

Третья ось на рис.3.14 не указана, множество Yвсегда можно получить как дополнение множествX,Zдо полного множества дисков.

Тогда путь 11 соответствует оптимальному решению задачи, а путь 101 - неоптимальному.

Рассмотрим случай n=2. Будем описывать элементы множеств в виде столбца цифр, соответствующих убыванию диаметра дисков:

XYZ

(,0,0) - исходное состояние,

(2,1,0) - 1-ый шаг,

(0,1,2) - 2-ой шаг,

(0,0,) - 3-ий шаг, целевое состояние.

Это оптимальное решение задачи - за 3 шага. Возможны также неоптимальные последовательности. Изобразим вначале все возможные последовательности следующим образом (рис.3.15):

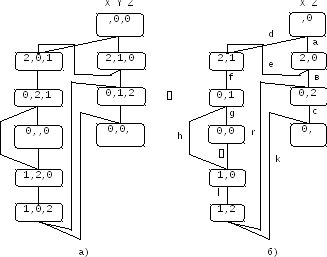
Рис.3.15. Возможные последовательности решения

задачи о ханойской башне для n=2

а) для трех множеств X,Y,Z, б) для двух множествX,Z

Представим теперь случай n=2 на координатной плоскости, используя координаты - множестваX,Z(первая и третья координаты). Получим рис.3.16, на котором отмечены дуги, соответствующие рис.3.15б. Видно, что этот граф как бы содержит в себе три графа дляn=1, а оптимальное решение соответствует последовательности дуг а,в,с (,0;2,0;0,2;0,).

Общий способ решения задачи о ханойской башне может быть получен путем анализа трансформации графа для nдисков при переходе кn+1 диску.

Граф в задаче о ханойской башне имеет ту особенность, что все ребра имеют одинаковую длину, равную единице, что соответствует одному шагу состояния дискретной системы.

Рис.3.16. Представление графом задачи

о ханойской башне для n=2