5.3.Виды дисперсий в совокупности, разделенной на группы. Правило сложения дисперсий.

Можно определить 3 показателя вариации признака совокупности:

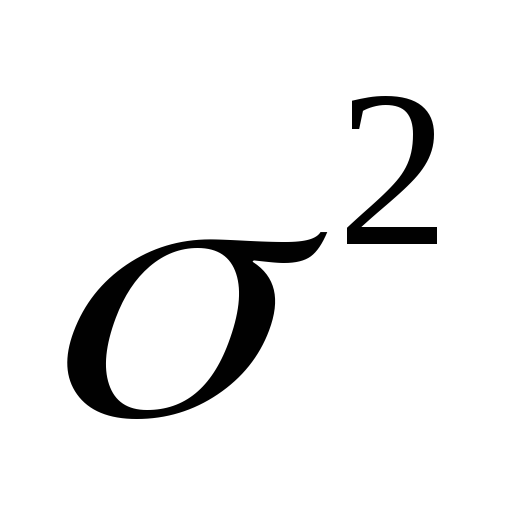1. ₀– общая дисперсия;

2. ² _Х – межгрупповая дисперсия;

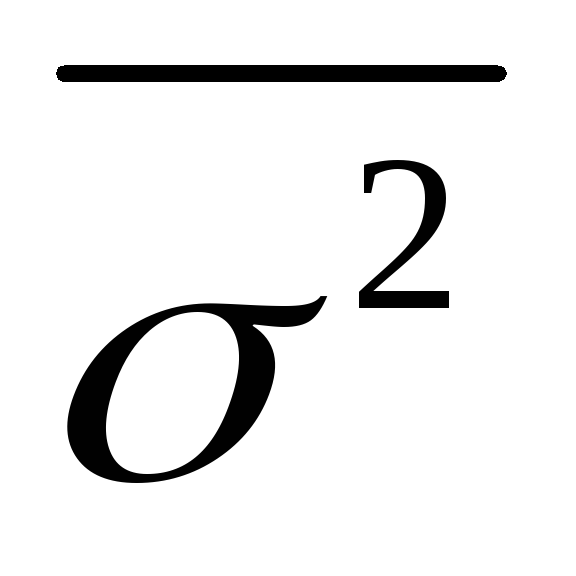3. – средняя из внутригрупповых дисперсий.

Рассмотрим их:

1) Общая дисперсия

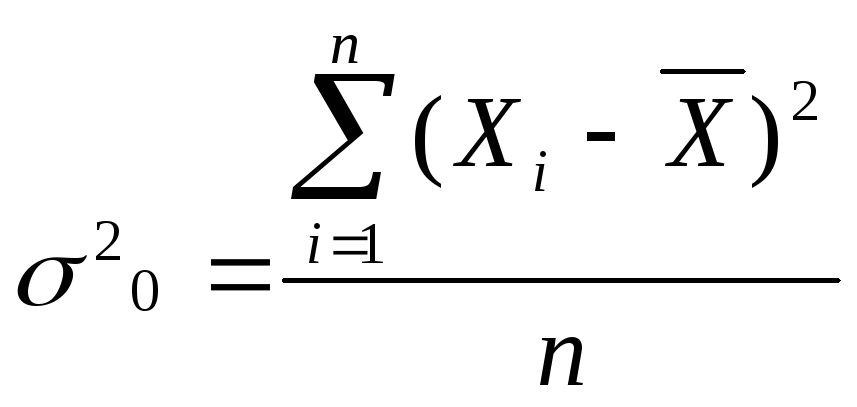
2) Межгрупповая дисперсия

Характеризует вариацию изучаемого признака, возникающую под влиянием признака-фактора, положенного в основание группировки.

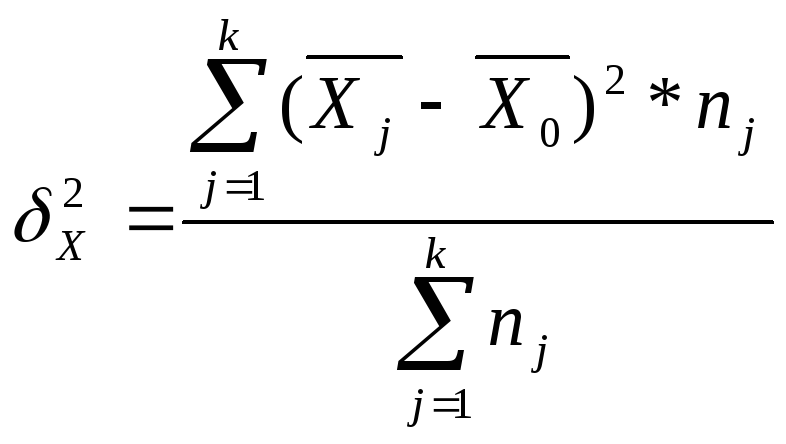
где к - число групп

n_j- число единиц вj-ой группе

- среднее поj-ой группе

- среднее по всей совокупности

3) Внутригрупповая дисперсия

Внутригрупповая дисперсия отражает часть вариации, происходящей под влиянием неучтенных факторов, которая не зависит от группировочного признака.

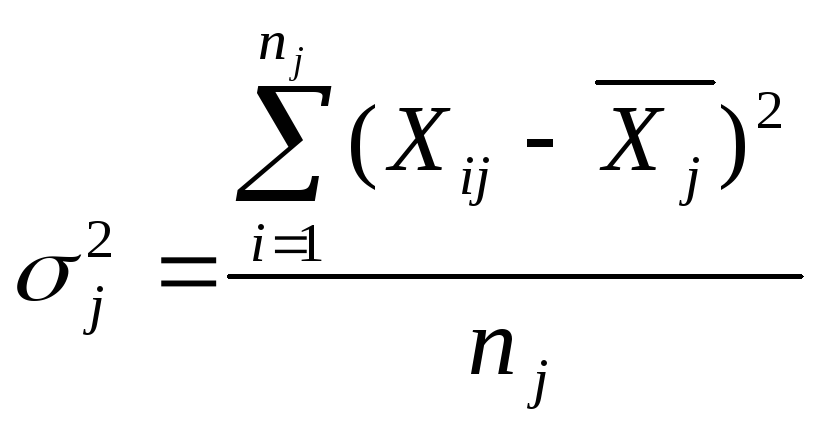
Средняя из внутригрупповых дисперсийпо совокупности в целом - вариация значений признака под влиянием прочих факторов.

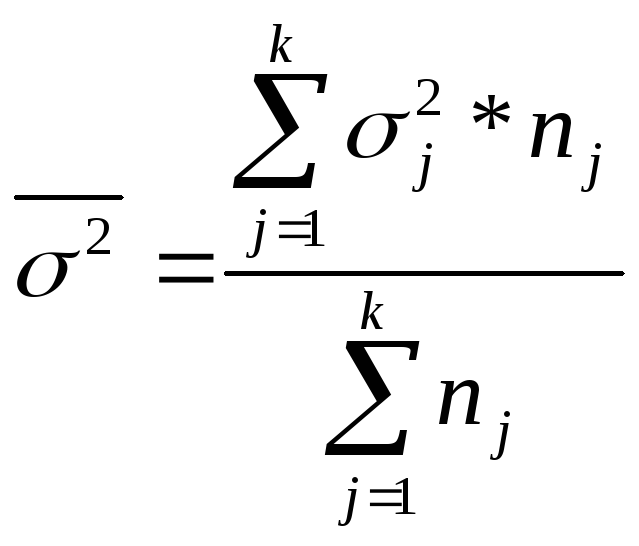
Правило сложения дисперсий: общая дисперсия, которая возникает под влиянием всех факторов, равна сумме средней из внутригрупповых и межгрупповой:

Эмпирическое корреляционное отношение показывает какая доля общей дисперсии приходится на дисперсию, обусловленную вариацией группировочного признака.

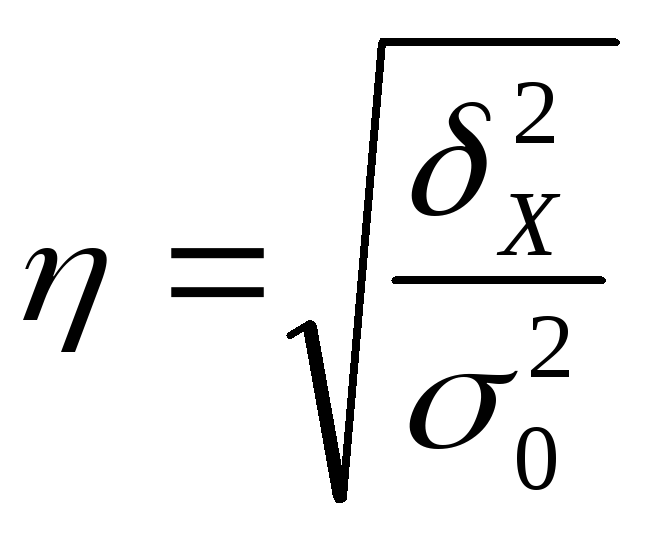
[0;1]. В случае =0 группировочный признак не влияет на результат, если=1, то результативный признак изменяется только в зависимости от группировочного признака, влияние прочих факторов на него равно 0.

§6. Выборочное наблюдение.

ОПР:Выборочнымназывается такое несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой совокупности.

Получаемые в процессе исследования результаты с определенной вероятностью распределяются на всю генеральную совокупность.

Генеральной совокупностьюназывается вся исходная изучаемая статистическая совокупность, из которой формируется выборка.

Отбор единиц может быть повторным и бесповторным.

При повторном отборепопавшая в выборку единица подвергается регистрации, а затем возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Число единиц генеральной совокупности, участвующих в отборе, остается в этом случае постоянным. На практике повторный отбор обычно используют в тех случаях, когда объем генеральной совокупности неизвестен. Например, при проведении маркетинговых исследований мы не можем точно оценить количество покупателей супермаркета, т.к. один и тот же покупатель может дважды прийти в этот магазин.

При бесповторном отборепопавшая в выборку единица подвергается исследованию и в дальнейшей процедуре отбора не участвует. Такой отбор происходит, если объем генеральной совокупности четко определен. Получаемые в этом случае результаты являются более точными, чем при повторном отборе.

В выборочную совокупность могут отбираться не только отдельные единицы, но и группы единиц. В первом случае отбор называется индивидуальным, а во втором - групповым.

Ошибки репрезентативности обусловлены тем, что выборочная совокупность не может соответствовать по всем параметрам генеральной совокупности. Средняя ошибка выборки:

где -дисперсия генеральной совокупности

n– объем выборки

На практике неизвестна, поэтому при.

При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки. Вероятность предельной ошибки подчиняется нормальному закону:

P(t)=F(t),

где - ошибка,

t-двукратная средняя ошибка выборки.

Обычно берут при t=2p=0,954.

В зависимости от состава и структуры генеральной совокупности выбирается вид выборки. К наиболее распространенным на практике видам относятся:

1) Простая случайная выборка.

2) Систематическая выборка (выборка из генеральной совокупности, которая упорядочена).

3) Типическая выборка (происходит из генеральной совокупности, разделенной на группы).

4) Серийная выборка (из генеральной совокупности происходит отбор целых групп, внутри которых производится сплошное исследование).

Методы отбора единиц в выборочную совокупность.

Формирование выборочной совокупности должно быть основано на принципе случайности. Опишем один из методов обеспечения данного принципа.

Метод случайной сортировки.

1) Каждой единице генеральной совокупности присваивается случайное число, получаемого с помощью датчика случайных чисел, находящихся от 0 до 1.

2) Единицы генеральной совокупности ранжируются в соответствии с полученным числом.

3) Отбираются первые mединиц.

Простая случайная выборка.

Данная выборка заключается в отборе единиц из генеральной совокупности без разделения ее на группы или серии, при этом средней ошибкой повторной выборки будет:

С учетом выбранного уровня вероятности считается предельная ошибка и оценивается среднее для выборки:

где - среднее по выборке,

- среднее по генеральной совокупности.

Если выборка без повтора, то

где n- объем выборки,

N- объем генеральной совокупности.

При подготовке выборочного наблюдения необходимо определить минимальный необходимый объем выборки, который обеспечит требуемую точность при данном уровне вероятности.

Таким образом, минимально возможный объем выборки с повторениями:

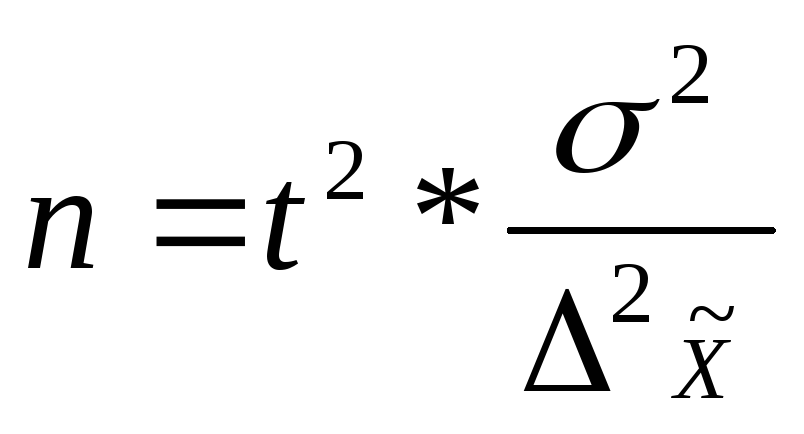
Аналогично, для выборки без повторений получим:

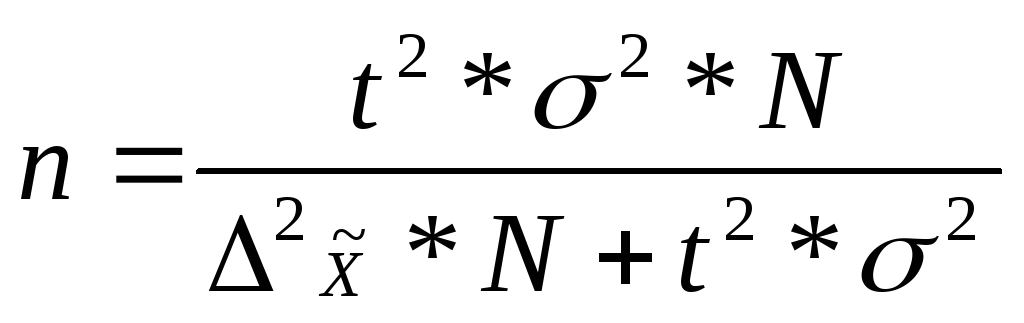
Расчет необходимого объема выборки предполагает, что на начальном этапе проведения выборочного наблюдения мы обладаем информацией о вариации изучаемых признаков. Источником этой информации могут быть:

1. Результаты исследования объекта за предшествующий период.

2. Результаты исследования аналогичных объектов.

3. Специально проведенное небольшое по объему выборочное исследование данного объекта, целью которого является лишь изучение вариации.