§7. Методы изучения связи социальных явлений.

Важной задачей статистики является разработка методики оценки связи социальных явлений. Решение этой задачи осложняется тем, что многие социальные явления не измеряются количественно, а носят качественный характер.

Для характеристики связей таких явлений используется метод информативных коэффициентов. Информационной базой для такого анализа служат данные различных социальных опросов, проводимые с помощью анкетирования.

Для оценки связей используется целый ряд показателей.

7.1. Коэффициенты оценки связи качественных признаков, представленных двумя градациями.

Для определения связи двух качественных признаков, каждый из которых состоит из двух групп, применяются коэффициенты ассоциации и контингенции.

Данные для анализа расписываются в виде таблиц сопряженности, т.е. для вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака.

Например, хороший и плохой.

a	b	a+b
c	d	c+d
a+c	b+d	a+b+c+d

(2 признака принимают только 2 значения)

Коэффициент ассоциации:

Коэффициент контингенции:

Если К_А≥0.5 и К_К≥0.3 , то связь считается подтвержденной.

Пример: В одном из отделений Сбербанка исследовалась связь между наличием вклада и семейным положением вкладчика. Результаты обследования характеризуются следующими данными:

Семейное положение	Имеют сбережения	Не имеют сбережения	Число вкладчиков
Одинокие	250	150	400
Семейные	800	450	1250
Итого	1050	600	1650

Вычислим

Таким образом, можно сделать вывод, что наличие или отсутствие сбережений не зависит от семейного положения.

7.2. Коэффициенты оценки связи качественных признаков, представленных несколькими градациями.

Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи используются коэффициенты взаимной сопряженности Пирсона и Чупрова.

В общем виде таблица имеет вид:

X \ Y	I	II	III	Всего
I			nxy	nx
II
III
Итого			ny

Коэффициент Пирсона:

Коэффициент Чупрова:

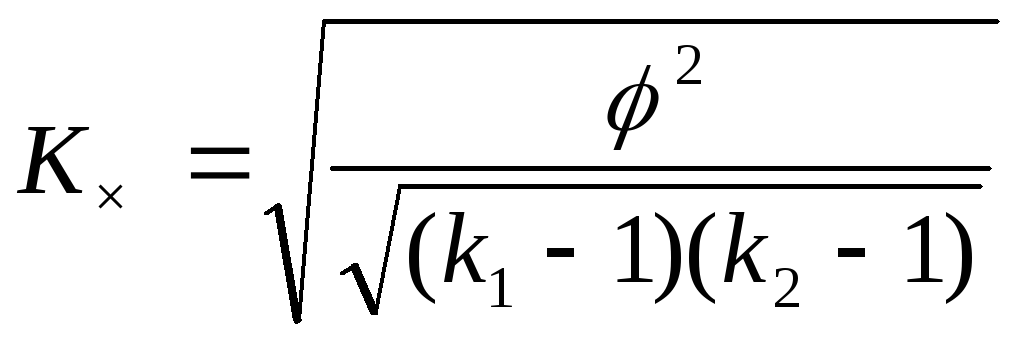
где к₁–число значений первого признака; к₂–число значений второго признака.

Пример:С помощью коэффициентов взаимной сопряженности проанализировать зависимость распределения сотрудников строительной фирмы по категориям от уровня их образования.

Образование	Руководители	Служащие	Рабочие	Итого
Высшее	10	30	50	45
Неполное высшее	7	25	10	42
Средн. спец.	2	15	50	67
Средн. общее	1	10	25	36
Итого	20	80	90	190

Вычислим

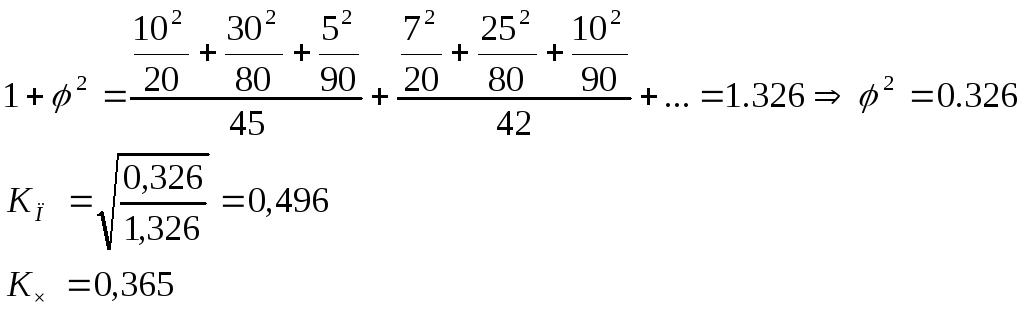
Считается, что если К_П≈ 0.5, то связь умеренная.