5.1. Показатели вариации и способы их расчета.

Для того, чтобы охарактеризовать степень рассеяния отдельных значений признака вокруг его среднего значения, в статистике используются показатели вариации.

Показатели вариации делятся на 2 группы:

1. Абсолютные

- размах вариации;

- среднее линейное отклонение;

- дисперсия;

- среднее квадратическое отклонение;

2) Относительные

- коэффициенты осцилляции;

- коэффициенты вариации;

- относительные линейные отклонения.

Относительные показатели вычисляются как отношение абсолютных показателей к среднему арифметическому или медиане.

Рассмотрим их:

1) Вариационный размах (амплитуда колебаний).

Показывает насколько велико различие между единицами совокупности, имеющими наименьшее и наибольшее значения признаков

R=X_max-X_min

К недостаткам этого показателя можно отнести тот факт, что очень низкое(или высокое) значение признака может быть вызвано какими-то случайными факторами, т.е. иметь аномальный характер. В этих случаях размах вариации дает искаженную амплитуду колебания признака. Прежде всего поэтому необходимо очистить наблюдения от различных выбросов.

2) Среднее линейное отклонение.

Простая формула: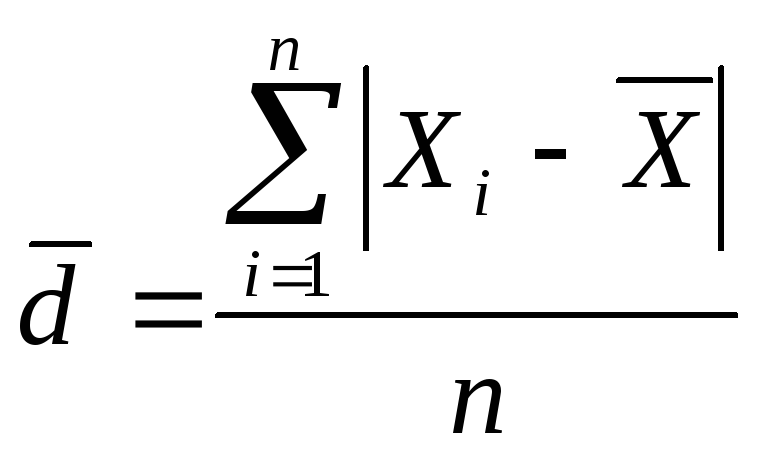

Взвешенная формула:

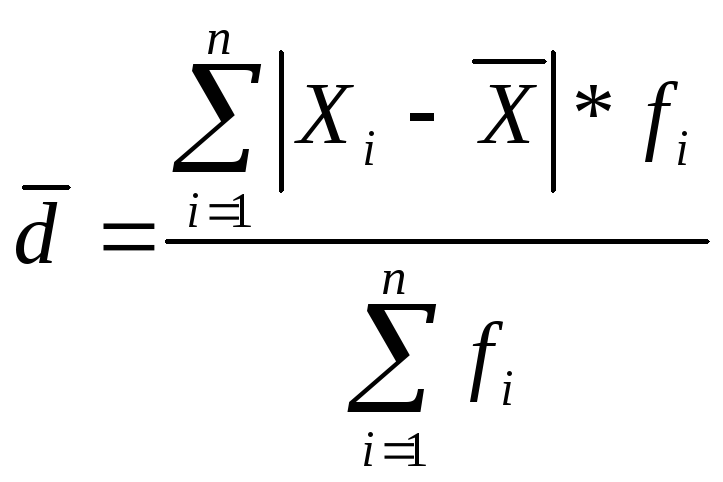
3) Дисперсия.

Простая формула: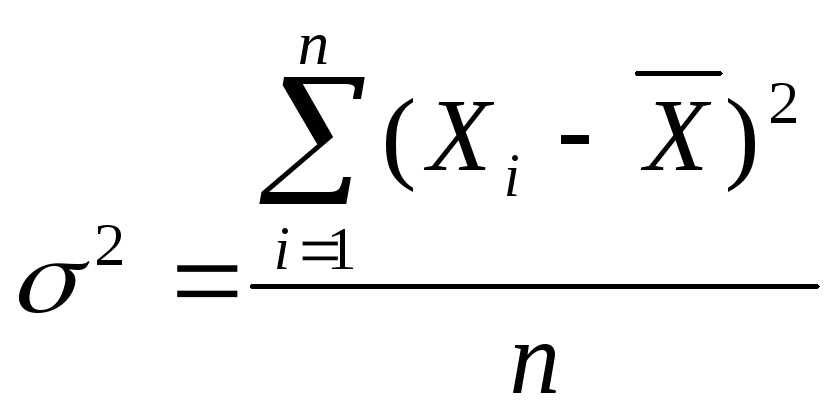

Взвешенная формула:

4) Коэффициент осцилляции.

Отношение размаха вариации к средней величине:

5) Линейный коэффициент вариации.

6) Коэффициент вариации.

Используется для оценки однородности совокупности близкой к нормальной, при этом совокупность считается однородной, если 33%.

5.2. Вариация альтернативного признака. Энтропия распределения.

В ряде случаев возникает необходимость в измерении дисперсии альтернативных признаков, т.е. тех признаков, которыми обладают одни единицы совокупности и не обладают другие.

Пример: Бракованная продукция; работа по получаемой специальности.

Значения альтернативного признака обычно задается 0, если объект этим признаком не обладает, и 1 ,если объект этим признаком обладает.

Пусть p=m/n– доля единиц совокупности, обладающих признаком, а

q- доля единиц совокупности, не обладающих этим признаком

p+q=1

Тогда среднее значение альтернативного признака:

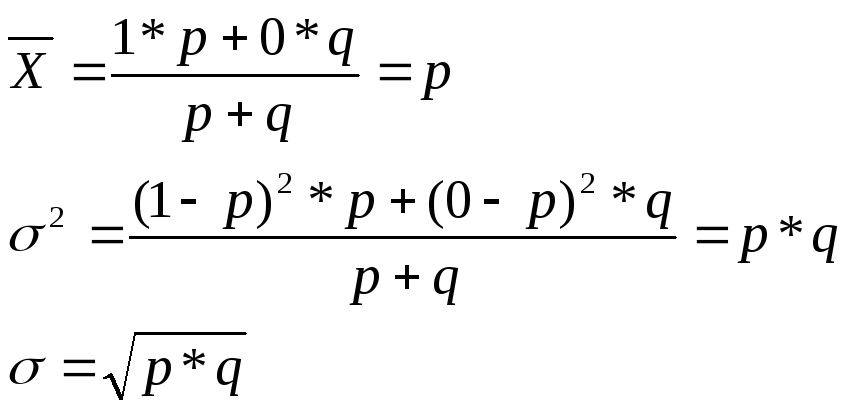
Максимальное значение дисперсии _max=0,25 при р=0,5.

Данные показатели могут быть использованы, например, для расчета среднего процента бракованной продукции при статистическом приемочном контроле.

Обобщенной характеристикой различий внутри ряда служит энтропия распределения.

ОПР:Энтропия- мера неопределенности данных наблюдений.

Она зависит от числа проявляющегося признака и от вероятности каждого из них.

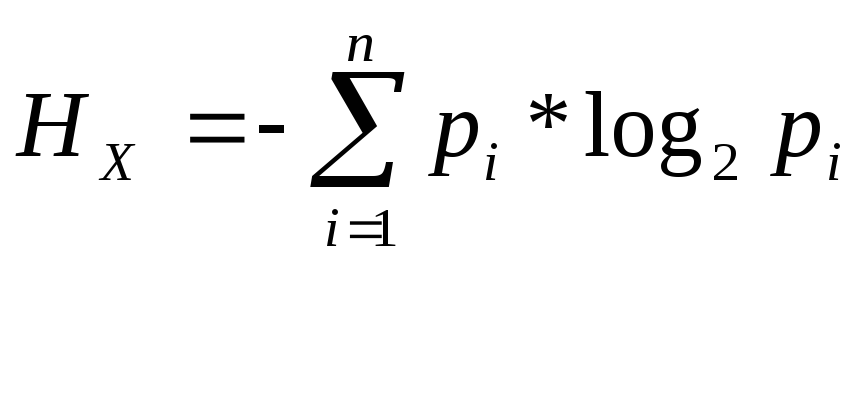
где р_i–вероятности различных значений случайных величин.

Если все варианты равновероятны, то энтропия максимальна. Например, при n=2 иp=0.5=1. Показатель энтропии позволяет также измерять количество информации. Чем больше вероятность случайного события, тем меньше информации несет его осуществление, т.е. в случаеp=1=0.