
- •§1. Статистика как наука.
- •1.1 Понятие статистики.
- •История статистики
- •1.2. Основные черты предмета статистической науки.
- •1.3. Метод статистической науки.
- •Первичная обработка, сводка и группировка результатов наблюдений
- •2.2. Основные организационные формы, виды и способы статистического наблюдения.
- •Отчетность предприятий, организаций и учреждений
- •Специально организованное статистическое наблюдение
- •Регистровая форма
- •2.3. Точность статистического наблюдения
- •§3. Статистическая сводка и группировка.
- •3.1. Задачи сводки и ее содержание.
- •3.2. Метод группировки.
- •3.3. Виды статистических группировок.
- •3.4. Принципы построения статистических группировок.
- •Ряды распределений
- •§4. Статистические показатели.
- •4.1. Виды статистических показателей.
- •4.2 Средние показатели.
- •Заработная плата работников предприятия
- •Распределение работников предприятия по возрасту.
- •Другие виды средних.
- •§5. Показатели вариации и анализ частотных распределений.
- •5.1. Показатели вариации и способы их расчета.
- •5.2. Вариация альтернативного признака. Энтропия распределения.
- •5.3.Виды дисперсий в совокупности, разделенной на группы. Правило сложения дисперсий.
- •§6. Выборочное наблюдение.
- •§7. Методы изучения связи социальных явлений.
- •7.1. Коэффициенты оценки связи качественных признаков, представленных двумя градациями.
- •7.2. Коэффициенты оценки связи качественных признаков, представленных несколькими градациями.
- •7.3. Бисериальный коэффициент корреляции
- •§8. Экономические индексы.
- •Индивидуальные и общие индексы.
- •Средние индексы.
- •§9. Выбор базы и весов индексов.
- •Индексы структурных сдвигов.
- •§10. Индексы Ласпейреса и Пааше.
4.2 Средние показатели.
В основном используются среднее арифметическое, среднее гармоническое, среднее геометрическое, среднее квадратическое.
Все перечисленные виды средних, кроме квадратических, можно в общем случае записать в следующей форме:
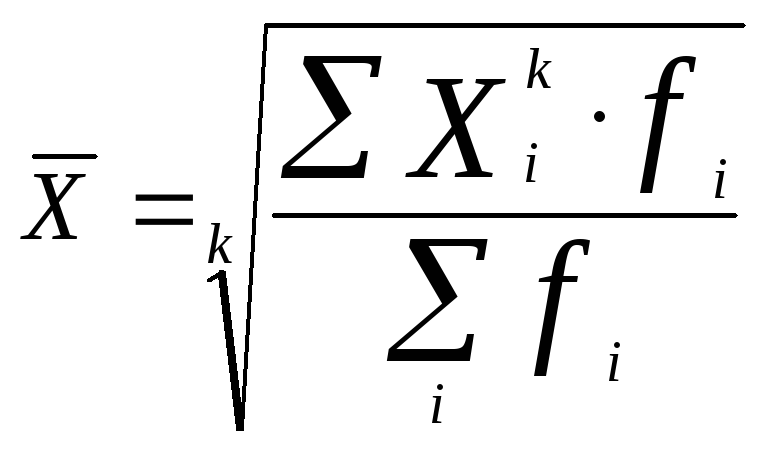
где
![]() - вариант признака, а
- вариант признака, а![]() - вес данного варианта.
- вес данного варианта.
1) Средняя арифметическая (простая)
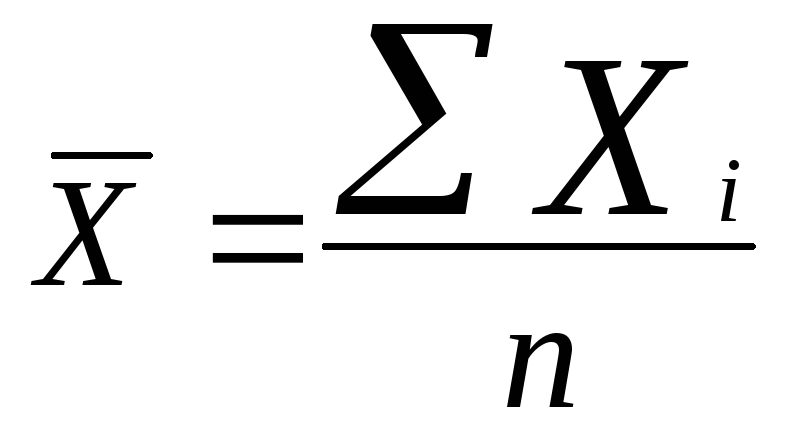
Эта формула используется в случаях, когда расчет происходит по не сгруппированным данным. Например: средний стаж работников в каком-либо предприятии.
2) Средняя арифметическая (взвешенная)
При расчете средних величин отдельные значения признака могут повторятся по нескольку раз. В этом случае расчет средних производится по сгруппированным данным. Пример:продажа акций.
|
Сделка |
Количество проданных акций |
Курс продажи акций |
|
1 |
500 |
1080 |
|
2 |
300 |
1050 |
|
3 |
1100 |
1145 |
Надо найти средний курс продаж (по таблице). Ищем по формуле средней арифметической взвешенной:
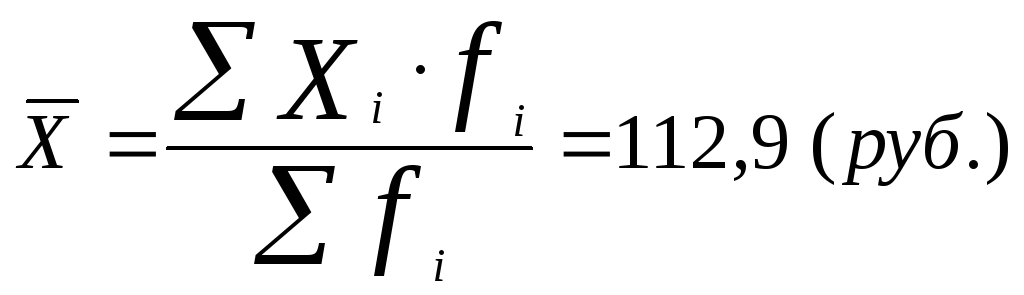
На практике часто допускаются ошибки при расчете средних величин, которые заключаются в игнорировании весов. Пример:
Заработная плата работников предприятия
|
Цех |
Средняя з/п в руб. |
|
1 |
4300 |
|
2 |
4100 |
Допустим, хотим посчитать среднюю з/п на всем предприятии.
![]() => эта формула
неверна, т.к. не учитывает количество
рабочих.
=> эта формула
неверна, т.к. не учитывает количество
рабочих.
Использовать среднее арифметическое простое можно только тогда, когда точно установлено отсутствие весов или их равенство.
Рассмотрим расчет среднего арифметического по интервальному вариационному ряду.
Распределение работников предприятия по возрасту.
|
Возраст |
Число работников |
|
до 25 |
7 |
|
25 – 30 |
13 |
|
30 – 40 |
38 |
|
40 – 50 |
42 |
|
50 – 60 |
16 |
|
60 и более |
5 |
|
Итого: |
121 |
Для определения среднего возраста найдем середины возрастных интервалов. При этом величины открытых интервалов условно приравниваются к величинам примыкающих к ним интервалов. Т.о. получаем:
22,5 27,5 35 45 55 65
Далее применяем формулу для средней арифметической взвешенной:
![]()
Другие виды средних.
Часто используется средняя гармоническая взвешенная.
Пример:валовой сбор и урожайность зерновых культур по областям. Нужно определить среднюю урожайность – это общий валовой сбор зерна на общую посевную площадь.
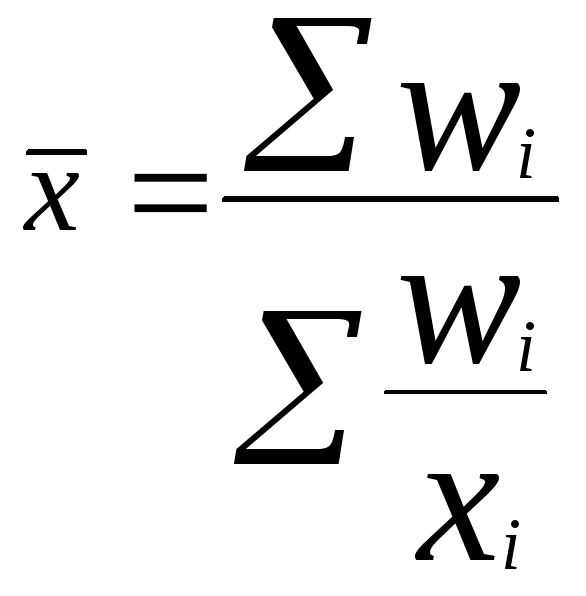
где
![]() - урожайность,
- урожайность,![]() - валовой сбор.
- валовой сбор.
§5. Показатели вариации и анализ частотных распределений.
Все показатели вариации можно разделить на три группы:
1) Показатели центра распределения: средняя арифметическая, мода, медиана.
2) Показатели степени вариации: вариационный размах, среднее линейное отклонение, дисперсия, коэффициент вариации.
3) Показатели типа распределения: структурные характеристики, показатели ассиметрии, кривые распределения.
Модой распределения(![]() )
называется такая величина изучаемого
признака, который в данной совокупности
встречается наиболее часто. Рассмотрим
определение моды по не сгруппированным
признакам.
)
называется такая величина изучаемого
признака, который в данной совокупности
встречается наиболее часто. Рассмотрим
определение моды по не сгруппированным
признакам.
Пример: рабочие бригады из 11 человек имеют следующие тарифные разряды:
5, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5.
=>
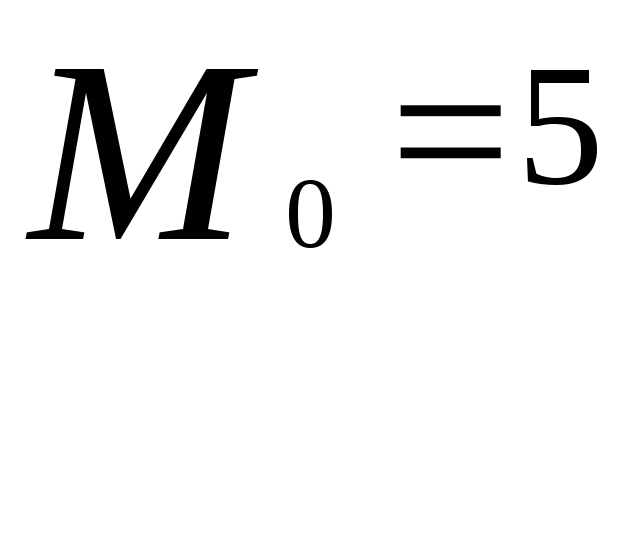
Модальный интервал, т.е. интервал содержащий моду, в случае интервального распределения с равными интервалами определяется по наибольшей частоте, с неравными интервалами – по наибольшей плотности. А мода определяется по формуле:
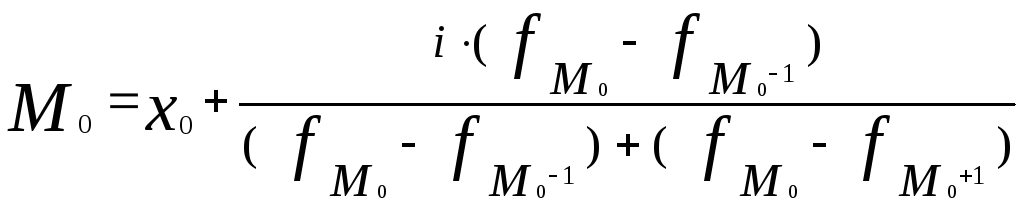
где
![]() - нижняя граница модального интервала;
i – величина модального интервала;
- нижняя граница модального интервала;
i – величина модального интервала;![]() - частота модального интервала;
- частота модального интервала;![]() - частота интервала предшествующего
модальному;
- частота интервала предшествующего
модальному;![]() - частота интервала следующего за
модальным.
- частота интервала следующего за
модальным.
В качестве характеристик вариационного
ряда используется медиана(![]() ).
).
Медиана – это величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от других величин:
![]()
Если в вариационном ряду 2m+1 случаев, то
![]() =
=![]()
Если в вариационном ряду 2m случаев, то
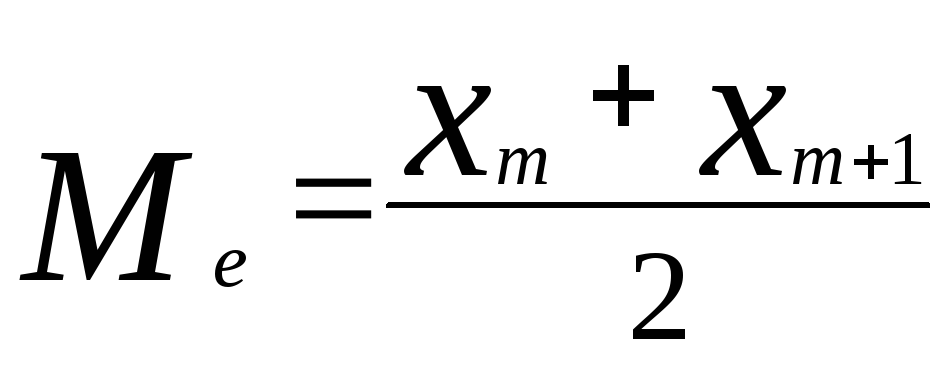
![]() практически играет роль средней величины
для неоднородной совокупности не
подчиняющейся нормальному закону.
практически играет роль средней величины
для неоднородной совокупности не
подчиняющейся нормальному закону.
Пример:пусть нам необходимо дать характеристику среднего дохода группы людей из 100 человек, 99 из которых имеют доход от 100 до 200$ в месяц, а 1 - 50000$ в месяц.
|
№ |
1 |
2 |
… |
99 |
100 |
|
Доход |
100 |
104 |
… |
200 |
50000 |
![]() =>объективно.
=>объективно.
![]() =>это неправильно.
=>это неправильно.
