1.4. Минимизация функций алгебры логики по методу Квайна - Мак-Класки

Недостаток метода Квайна - необходимость исчерпывающего попарного сравнения или сопоставления всех минтермов на этапе нахождения первичных импликант. С ростом числа минтермов увеличивается количество попарных сравнений.

Метод Квайна - Мак-Класки представляет собой формализованный на этапе нахождения простых импликант метод Квайна. Формализация выполняется следующим образом[2]:

1. Все минтермы из СДНФ булевой функции записываются их двоичными номерами.

2. Все номера разбиваются на непересекающиеся группы. Признак образования -й группы: наличиеединиц в каждом двоичном наборе минтерма.

3. Склеивание производится только между номерами соседних групп. Склеиваемые номера отмечаются каким-либо знаком.

4. Склеивания производят всевозможные, точно так, как и в методе Квайна.

Минтермы, подлежащие склеиванию, различаются только по одной переменной, а их коды - только в одном разряде. По этой причине сравнению подлежат только двоичные коды минтермов соседних групп. Группы кодов, различающиеся в двух или большем количестве разрядов, просто нет смысла сравнивать.

Нахождение минимальных ДНФ производится по импликантной таблице, как и в методе Квайна. Применение метода Квайна – Мак-Класки рассмотрим на следующем примере.

Пример 1.4. Пусть булева функция задана таблицей истинности (таблица 1.4). Нахождение минимальных ДНФ производится по этапам.

Таблица 1.4

Таблица истинности четырех переменных

	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
	0	1	0	1	0	1	0	1	0	0	0	0	0	0	1	1

1. В СДНФ функции заменим все минтермы их двоичными номерами:

2. Образуем группы двоичных номеров. Признаком образования -й группы является наличиеединиц в двоичном номере минтерма (см. табл. 1.5).

3. Склеиваем номера из соседних групп. Результаты склеивания запишем в табл. 1.6. Так из групп 1 и 2 табл. 5 образовалась группа 1 в табл. 1.6, а из групп 2 и 3 табл. 1.5 получили группу 2 табл. 1.6 и, наконец, из групп 3 и 4 табл. 1.5 получили группу 3 табл. 1.6.

Обычно склеиваемые номера зачеркивают. Продолжим операцию склеивания и склеим теперь номера групп в табл. 1.6. Склеиваться теперь могут только те номера, в которых звездочка расположена на одинаковой позиции.

Таблица 1.5 Таблица групп двоичных номеров

Таблица 1.6 Таблица склеенных групп двоичных номеров

Склеиваемые номера опять вычеркнем. Результат склеивания первых двух групп (табл. 1.6) позволил получить простую импликанту .

4. Итак, в результате выполнения операции склеивания получено три простые импликанты .

5. Строим импликантную матрицу (табл. 1.7).

Таблица 1.7

Импликантная матрица

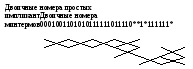
По таблице определяем совокупность простых импликант исоответствующих минимальной ДНФ. Для восстановления буквенного вида простой импликанты достаточно выписать произведения тех переменных, которые соответствуют сохранившимся двоичным цифрам:;.