4.6. Способы описания алгоритмов и микропрограмм

Наиболее наглядно изображать микропрограммы и алгоритмы в виде ориентированного графа, который называют граф-схемой алгоритма (ГСА). Кроме наглядности это дает возможность использовать для анализа и преобразования микропрограмм эффективные методы теории графов. При графическом описании отдельные функции алгоритмов (микрооперации) отображаются в виде условных графических изображений или вершин [3].

Граф микропрограммы состоит из совокупности перечисленных вершин и дуг, соединяющих выходы одних вершин с входами других. Соединение вершин и направление дуг графа определяют исходя из алгоритма операции, описываемого графом, и структуры операционного автомата. Сама микропрограмма и ее граф должны быть корректны, т.е. отвечать следующим условиям:

1. В графе должна быть только одна начальная и одна конечная вершина.

2. В любую вершину графа должен вести, по крайней мере, один путь из начальной вершины.

3. Из каждого выхода любой вершины графа должен существовать, по крайней мере, один путь в конечную вершину.

4. При всех возможных значениях логических условий и используемых слов должен существовать путь из начальной вершины в конечную вершину.

На основе данных микрокоманд и производится разработка графа микропрограммы. Граф микропрограммы представляет собой ориентированный граф, содержащий одну начальную, одну конечную и произвольное множество промежуточных вершин - операторных и условных. Операторная вершина соответствует одной микрокоманде, а условная - проверяемому логическому условию (флагу). При построении графа микропрограммы необходимо руководствоваться следующими правилами:

1. входы и выходы различных вершин соединяются дугами с указанием направления передачи информации;

2. каждый выход соединяется только с одним входом;

3. для любой вершины графа существует, по крайней мере, один путь из нее к конечной вершине.

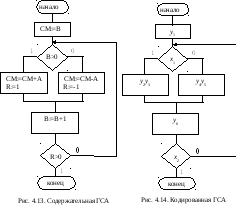
ГСА называется содержательной (рис. 4.13), если внутри вершин записаны в явном виде микрооперации и логические условия . Если же каждую микрооперацию обозначить символом , a логические условия через, то получится так называемая кодированная ГСА (рис. 4.14). Для правильного восприятия микропрограммы, заданной в виде кодированной ГСА, необходимо знать соответствия между ,и содержанием соответствующих микроопераций и логических условий.

Абстрактный синтез микропрограммного автомата по ГСА осуществляется в два этапа: a) получение отмеченной ГСА; b) построение графа автомата или таблиц переходов и выходов. Одну и ту же ГСА можно представлять как автоматом Мили, так и автоматом Мура.

4.8. Синтез автомата Мили

На этапе получения отмеченной ГСА входы вершин, следующих за операторными, отмечают символами a₁, a₂, … по следующим правилам:

1) символом отмечают вход вершины, следующей за начальной вершиной, а также вход конечной вершины;

2) входы всех вершин следующих за операторными вершинами, должны быть отмечены;

3) входы различных вершин, за исключением конечной вершины, отмечаются различными символами;

4) если вход вершины отмечается, то только одним символом.

Ясно, что для проведения отметок потребуется конечное число символов . Результатом первого этапа является отмеченная ГСА, которая служит основой для второго этапа - перехода к графу или таблицам переходов-выходов. Пример ГСА, отмеченной для автомата Мили, представлен на рис. 4.15.

На втором этапе используя отмеченную ГСА создают граф автомата или таблицы переходов-выходов. При этом полагают, что в автомате будет ровно столько состояний, сколько символов понадобилось при отметке ГСА.

Для каждого из состояний отмеченной ГСА определяем все пути, ведущие в другие состояния и проходящие только через одну операторную вершину. Например, из состояния имеется переход в состояниеи в состояние. Переходанет, так как этот путь не проходит ни через одну операторную вершину. Будем считать, что автомат осуществляет переход, например, извпри условии, и вырабатывает на этом переходе выходные сигналы(см. рис. 4.15). Это означает, что значения условий,,на этом переходе не оказывают влияния на автомат.

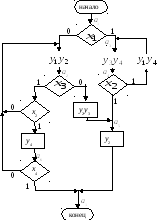
Рис. 4.15. Отмеченная ГСА автомата Мили

Исключение составляет только один путь, ведущий в конечную вершину, он может не содержать ни одной операторной вершины (например, переход из в), т.е. он не сопровождается выработкой выходных сигналов.

Отмечаем на графе все указанные пути для всех состояний в виде дуг, которым приписываем условия перехода и выходной сигнал, вырабатываемый на этом переходе. Получим граф автомата (рис. 4.16).

Рис. 4.16. Граф автомата Мили

На этом графе переходам типа ,приписывается условие перехода 1, т.к. эти переходы являются безусловными и выполняются всегда, когда автомат попадает в состояние(или).

Таблица 4.14 Прямая таблица переходов-выходов автомата Мили 1 1 -

Таблица 4.15 Обратная таблица переходов-выходов автомата Мили 1 - 1

На основании отмеченной ГСА или графа автомата можно построить таблицу переходов-выходов. Для микропрограммных автоматов таблица переходов-выходов строится в виде списка и различаются как прямая и обратная таблицы. Для данного автомата прямая таблица представлена табл. 4.14, а обратная - табл. 4.15.

В приведенных таблицах - исходное состояние,- состояние перехода,- условие (входной сигнал), обеспечивающий переход из состоянияв состояние,- выходной сигнал, вырабатываемый автоматом при переходе изв.