
Contents
1.1 |
........................................................................................................................................................................................... |
2 |
1.2 ........................................................................................................................................................................................... |
2 |
|
1.3 ........................................................................................................................................................................................... |
3 |
|
1.3.1 ........................................................................................................................................................................................ |
3 |
|
1.3.2 ........................................................................................................................................................................................ |
3 |
|
1.4 ........................................................................................................................................................................................... |
5 |
|
1.4.1 ........................................................................................................................................................................................ |
5 |
|
1.4.2 ........................................................................................................................................................................................ |
5 |
|
1.4.3 ........................................................................................................................................................................................ |
5 |
|
1.4.4 ........................................................................................................................................................................................ |
5 |
|
1.4.5 ........................................................................................................................................................................................ |
5 |
|
1.4.6 ........................................................................................................................................................................................ |
5 |
|
2.1 ........................................................................................................................................................................................... |
9 |
|
2.2 ......................................................................................................................................................................................... |
10 |
|
2.4. ........................................................................................................................................................................................ |
10 |
|
2.4.1 ...................................................................................................................................................................................... |
10 |
|
2.4.2 ...................................................................................................................................................................................... |
11 |
|
2.5 ......................................................................................................................................................................................... |
14 |
|
2.6 ......................................................................................................................................................................................... |
17 |
|
2.7 ......................................................................................................................................................................................... |
20 |
|
2.8 ......................................................................................................................................................................................... |
21 |
|
2.9 |
......................................................................................................................................................................................... |
23 |
2,10 ....................................................................................................................................................................................... |
26 |
|
2,11 ....................................................................................................................................................................................... |
27 |
|
2,12 ....................................................................................................................................................................................... |
31 |
|
2,13 ....................................................................................................................................................................................... |
33 |
|
2,14 ....................................................................................................................................................................................... |
37 |
|
2,15 ....................................................................................................................................................................................... |
40 |
|
Физика — это наука о природе в самом общем смысле. Она изучает различные субстации бытия (материю, вещество, поля) и наиболее простые формы её движения, а также фундаментальные взаимод. природы, управляющие движением материи.
Механика — область физики, изуч. движение материальных тел и взаимодействие между ними.
Кинематика — раздел механики, изучающий математическое описание движения тел без рассмотрения причин движения.
Динамика — раздел механики, в котором изучаются причины возникновения механического движения.
Основные абстрактные модели реальных тел
материальная точка – имеет массу, но не имеет размеров; абсолютно твёрдое тело – объём конечных размеров, сплошь заполненный веществом, причём расстояния между любыми двумя точками среды, заполняющей объём,
не изменяются во время движения
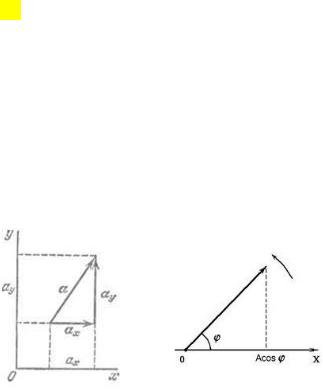
1.1 Скаляр - физческая величина , которая определяется только значением.
Вектор - физческая величина, которая определяется не только значением, но и направлением.
Изрброжение векторов
Геометрически вектор изображается как направленный отрезок прямой линии, длина которого в масштабе – модуль вектора.
Обозначение векторов
Векторная величина обозначается символом соответствующей физической величины со стрелкой над ней:  ,
, 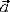 ,
,  . Модуль вектора обозначается символом без стрелки: |
. Модуль вектора обозначается символом без стрелки: |  | или V.
| или V.
1.2 составляющие вектора
Любой вектор можно представить как сумму нескольких векторов.
Замену одного вектора векторной суммой нескольких других называют разложением вектора на составляющие. Составляющие вектора, конечно, тоже векторы. Разложение вектора на составляющие можно произвести бесконечным числом способов, точно так же как любую скалярную величину можно разложить бесконечным числом способов на слагаемые.
Чаще всего производят разложение векторов по направлениям осей какой-либо определенной прямоугольной системы координат. Выбрав определенную систему координат, можно охарактеризовать вектор величиной и знаком его составляющих, уже не указывая их направления.
Проекция векторов
Величину составляющей, взятую со своим знаком, называют проекцией вектора на направление соответственной оси
Единичный вектор - это вектор, абсолютная величина которого равен единице.
Единичные векторы часто связывают с координатными осями системы координат (в частности, с осями декартовой системы координат). Направления этих векторов совпадают с направлениями соответствующих осей, а их начала часто совмещают с началом системы координат.

1.3 сложение вектров
Графическое сложение и вычитание. Правила треугольника и паралллеограмма. Вычитание векторов
Аналитической метод сложения и вычитания
1.3.1
1.3.2

.

Правило ломанной – замкнуть ломанную до многоугольника.
1.4 умножение векторов
1.4.1
1.4.2
1.4.3
1.4.4
1.4.5
1.4.6



4.Правило ломанной – замкнуть ломанную до многоугольника. |
10. Двойное векторное произведение |
||||||
|
|
|
|
|
|||
|
|
|
|
|
— векторное |
|
|
|
|
|
|
|
произведение вектора |
на векторное |
|
|
|
|
|
|
произведение векторов |
и |
|
5. Перевод задачи на координатный (аналитический) язык – и по |
|
|
|||||
координатам найти сумму и разность: |
|
|
|
|
|||
С=А+В, если Сх=Ах+Вх, Су=Ау+Ву… |
|
|
|
|
|||
|
|
|
|
|
11. Преобразование векторов при сдвиге: |
||
6. 1) |
; |
|
|
|
= + , X=ax+x’, y= ay+y’… |
|
|
|
|
|
при повороте: х=х’cosa – y’sina, |
||||
|
|
|
|
|
|||
|
|
|
|
|
y=x’sina+ y’ cosa |
|
|
2) |
, если |
и |
, если |
и |
при инверсии: х=-x’,y=-y’… |
||
псевдовекторы = аксиальные – координаты |
|||||||
|
|
|
|
|
|||
обозначается |
. |
|
|
|
изменяются на противоположные при |
||
|
|
|
инверсии систем координат |
||||
|
|
|
|
|
|||
|
|
|
|
|
истинный вектор = полярный – координаты |
||
|
|
|
|
|
не изменяются при инверсии систем |
||
|
|
|
|
|
координат |
|
|
|
|
|
|
|
|
||
7.Скалярным произведением двух векторов называется число, |
12. Производной функции f(x) в |
||||||
точке x0называется предел отношения |
|||||||
равное произведению модулей этих векторов на косинус угла |
|||||||
приращения функции f в этой точке к |
|||||||
|
|
|
|
|
|||
|
|
|
|
|
приращению аргумента |
х, |
|
между ними. |
|
. |
|
|
когда последнее стремится к нулю |
||
|
|
|
(бесконечно мало). Записывается так. |
||||
|
|
|
|
|
|||
Из физики известно, что работа силы F при перемещении S равна |
LimΔx→0 (Δf(x0)/Δx)=limΔx→0 ((f(x+Δx)- |
||||||
А=F•S•cosj т. е. А=(F•S). |
|
|
|
f(x0))/Δx)=f`(x0) |
|
||
Свойства: 1. |
|
|
|
|
Геометрический смысл |
|
|
|
|
|
|
производной. Производная в точке x 0 равна |
|||
|
|
|
|
|
|||
2. |
|
|
|
|
угловому коэффициенту касательной к |
||
|
|
|
|
графику функции y = f(x) в этой точке. |
|||
|
|
|
|
|
|||
3. |
|
|
|
|
|
|
|
4. |
|
|
|
|
13. Дифференцирование скаляров: |
||
14. Дифференцирование векторов:
8. Векторным произведением вектора на
вектор |
называется вектор |
который обладает следующими |
|
= |
|
|
I + |
|
j + |
|
k и т.д. |
|||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
свойствами: |
|
|
|
|
|
|
|
15. Интеграл - одно из важнейших понятий |
||||||||
Его длина равна |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
математики, возникшее в связи с |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
Вектор c перпендикулярен |
|
|
|
|
|
|
потребностью, с одной стороны, отыскивать |
|||||||||
|
к плоскости, в |
которой |
лежат |
функции по их производным (например, |
||||||||||||
вектора а и b |
|
|
|
|
|
|
|
находить функцию, выражающую путь, |
||||||||
|
|
|
|
|
|
|
|
|
пройденный движущейся точкой, по |
|||||||
Вектор |
направлен |
так, |
|
что |
поворот |
от вектора |
к |
скорости этой точки), а с другой - измерять |
||||||||
вектору |
осуществляется |
|
против |
часовой |
стрелки, |
если |
площади, объёмы, длины дуг, работу сил за |
|||||||||
|
определённый промежуток времени и т. п. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
смотреть из конца вектора (в этом случае, говорят, что тройка |
Интегрирование – процесс нахождения |
|||||||||||||||
интеграла. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
векторов |
и |
– правая). |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
16. Первообразная функция - функция, |
|||||||
|
|
|
|
|
|
|
|
|
производная от которой равна данной |
|||||||
Векторное произведение равно площади параллелограмма, |
|
|
функции на всей области определения. |
|||||||||||||
|
|
Неопределённый интеграл для функции - |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
построенного на векторах |
, |
|
|
|
|
|
это множество всех первообразных данной |
|||||||||
|
|
|
|
|
|
|
|
|
функции. |
|
|
|
|
|
||
9. Смешанным произведением трех векторов |
, |
|
|
Определенный интеграл от непрерывной |
||||||||||||
|
|
функции равен разности значений |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
, называется число, равное векторному произведению |
, |
|
неопределенного интеграла при верхнем |
|||||||||||||
|
и нижнем пределах. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
умноженному скалярно на вектор |
, то есть |
. |
|
|
Геометрический смысл определённого |
|||||||||||
|
|
интеграла. Если f(x) >0 на |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
отрезке [a,b], то интеграл равен площади |
|||||||
Смешанное произведение |
|
равно объему параллелепипеда, |
|
криволинейной трапеции ABCD, |
||||||||||||
|
|
ограниченной снизу отрезком [a,b], слева и |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
построенного на векторах |
, |
, |
|
|
|
|
справа - прямыми x = a и x = b, сверху – |
|||||||||
|
|
|
|
|
|
|
|
|
функцией y =f(x). |
|
|
|
||||

2.1 Понятие производной и дифферециала скалярной функции одной переменной.

2.2
2.4.
2.4.1

2.4.2


12. Производной функции f(x) в точке x0называется предел отношения приращения функции f в этой точке к приращению аргумента х, когда последнее стремится к нулю
(бесконечно мало). Записывается так.
LimΔx→0 (Δf(x0)/Δx)=limΔx→0 ((f(x+Δx)- f(x0))/Δx)=f`(x0)
Геометрический смысл
производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
13.Дифференцирование скаляров:
14.Дифференцирование векторов:
= |
|
I + |
|
j + |
|
k и т.д. |
|
|
|
15.Интеграл - одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой - измерять площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т. п. Интегрирование – процесс нахождения интеграла.
16.Первообразная функция - функция, производная от которой равна данной функции на всей области определения.
Неопределённый интеграл для функции - это множество всех первообразных данной функции.
Определенный интеграл от непрерывной функции равен разности значений
неопределенного интеграла при верхнем и нижнем пределах.
Геометрический смысл определённого интеграла. Если f(x) >0 на
отрезке [a,b], то интеграл равен площади криволинейной трапеции ABCD, ограниченной снизу отрезком [a,b], слева и справа - прямыми x = a и x = b, сверху – функцией y =f(x).
17.

2.5
Три способа задания движения.
Векторный способ.
Положение точки по отношению к системе отсчѐта (т.О)
задаѐтся радиусом-вектором, проведѐнным от начала отсчѐта до движущейся точки М.
Закон движения задаѐтся векторным уравнением:
Координатный способ.
При координатном способе положение точки задаѐтся какими-либо тремя координатами.
Если выбрана прямоугольная декартова система координат, то закон движения точки М задаѐтся тремя уравнениями:
x = f1(t)
y = f2(t)
z = f3(t)
Естественный способ.
- |
+ |
|
Этот способ применяется, обычно, если известна траектория |
|
О |
l |
М |
|
|
|
точки по отношению к выбранной системе отсчѐта. |
|||
|
|
|
Положение точки М определяется расстоянием |
от |
выбранного от траектории начала отсчѐта, измеренным вдоль траектории и взятым с соответствующим законом. Закон движения задаѐтся уравнением
 .
.
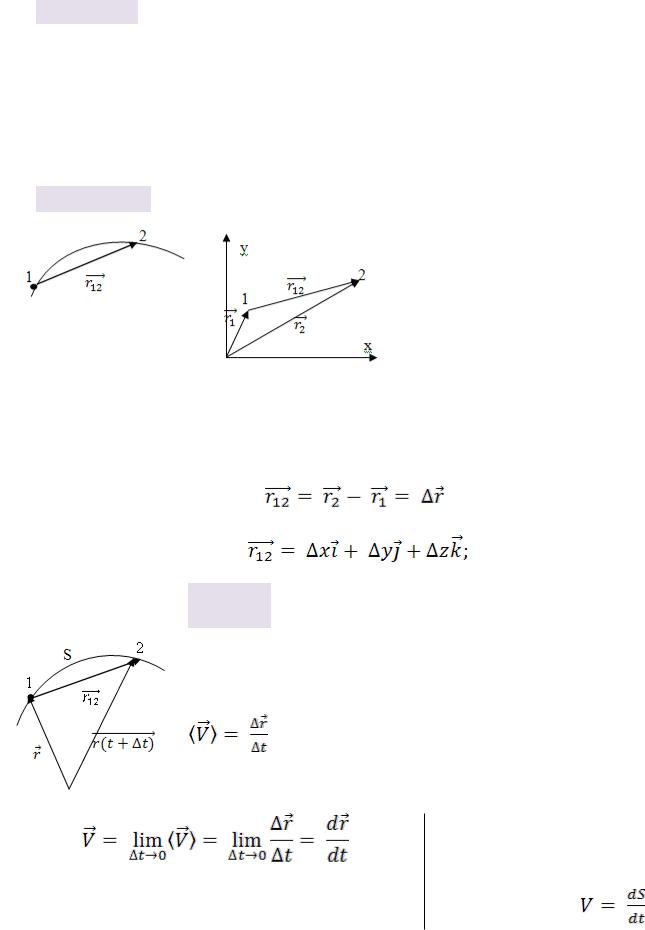
Траектория – непрерывная линия, которую описывает точка при своѐм движении. Уравнение траектории можно получить из кинематических уравнений движения, исключая из них время. Уравнение траектории связывает между собой координаты точек:
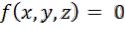 .
.
Перемещение – вектор, проведѐнный из начального положения точки в конечное.
Выражение вектора перемещения через приращения радиуса-вектора и координат
;
Скорость – 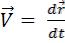 – производная радиуса-вектора
– производная радиуса-вектора
точки по времени.
Средняя скорость:
– отношение перемещения точки за время  k
k 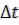 .
.
От средней скорости к скорости:
вектор скорости направлен по касательной к траектории;
модуль скорости
|
|
|
Проекции ускорения на нормаль ( |
) и тангенциаль |
|||
( |
|
|
) к траектории. |
|
|
|
|
|
|
|
Найдѐм проекции ускорения an и aτ. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(*) |
|
|
|
|
|
|
|
|
|
|
|
|
и |
– единичные векторы, |
направленные |
||
|
|
|
соответственно, к центру кривизны (т. О) и по |
||||
|
|
|
касательной к траектории. |
|
|
|
|
– проекция ускорения |
на касательную к траектории. |
|
|
|
|||
|
– касательное или тангенциальное ускорение. |
||||||
Первое слагаемое в |
(*) |
|
|||||
|
|
|
|
|
|
|
|
Полное ускорение: 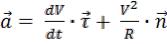
Модуль полного ускорения: 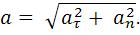
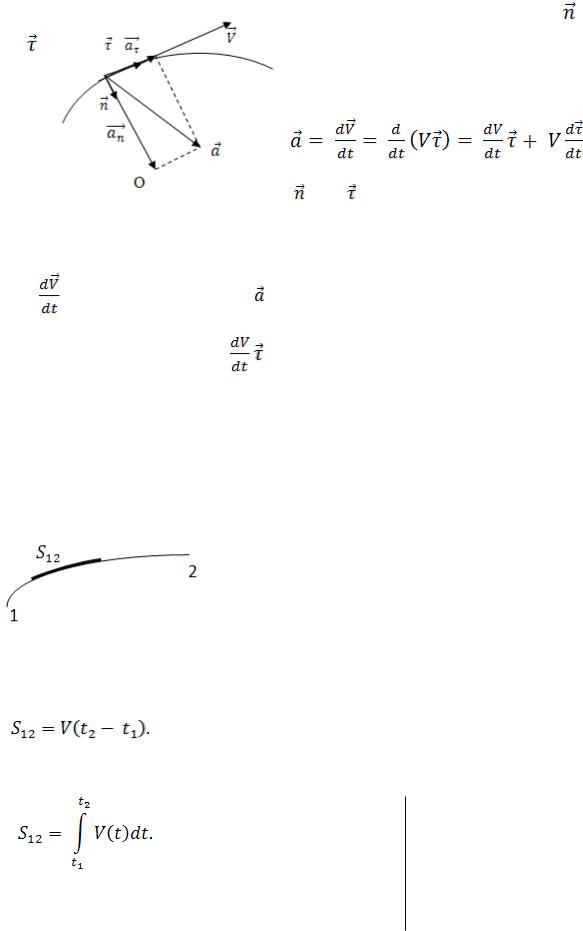
Путь – длина участка траектории, пройденного материальной точкой.
Вычисление пути.
При движении с постоянной по модулю скоростью путь, пройденный за время от 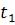 до
до 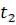
Если скорость не остаѐтся постоянной, то
Графическое пояснение
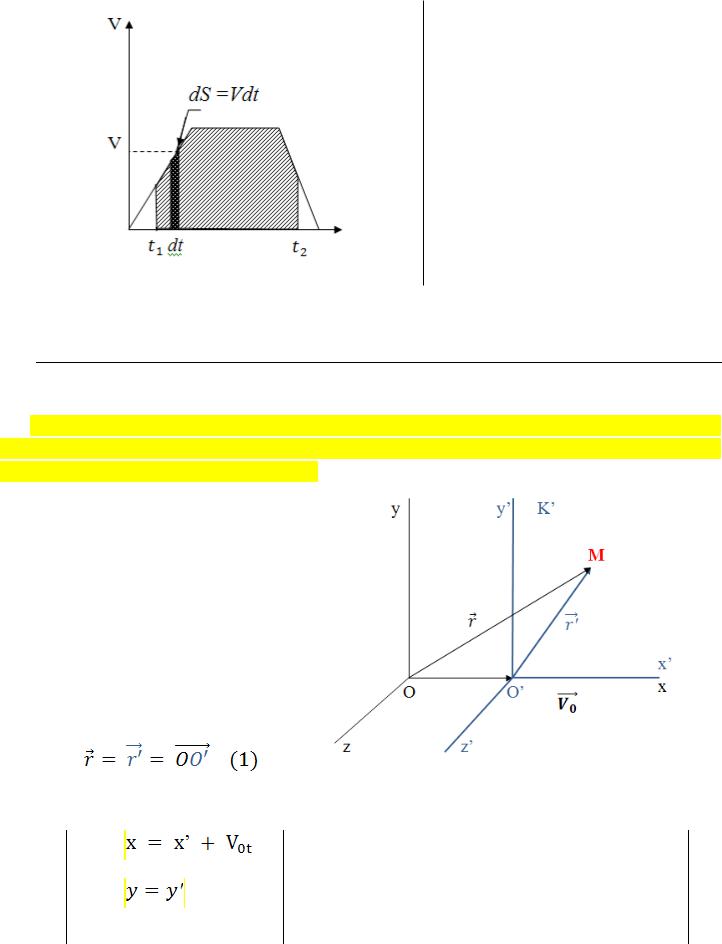
Замечание.
2.6 Переход в вращающую систему отсчета.
Преобразования Галилея: Это преобразования координат и времени при переходе от описания движения точки в одной инерциальной системе отсчѐта к описанию этого же движения в другой инерциальной системе.
Получим их.
K – условно неподвижная система.
K’ – движется относительно K с
постоянной скоростью  вдоль оси x.
вдоль оси x.
Отсчёт времени начался в момент, когда положения точек O и O’ совпадали.
Из рисунка видно:
В проекциях на оси координат:
Из этих преобразований следует, что расстояния между какими-либо
фиксированными точками 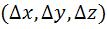 считаются одинаковыми во всех системах
считаются одинаковыми во всех системах
отсчёта, некоторые движутся относительно друг

друга с постоянной скоростью; интервалы времени между двумя событиями,
отсчитываемые в этих системах также одинаковы
Из соотношения (1), дифференцируя по времени радиусы-векторы точки M и вектор
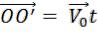 , получаем соотношения между скоростями и ускорениями точки М в обеих системах отсчёта:
, получаем соотношения между скоростями и ускорениями точки М в обеих системах отсчёта:
Преобразования (1) и (2) показывают, что координаты, скорость и, следовательно, другие кинематические характеристики точки (траектория, путь и пр.) зависят от выбора системы отсчёта, т.е. движения относительно.
Равенство (3) говорит о том, что законы механики во всех инерциальных системах одинаковы. Действительно, ускорение точки определяется основным уравнением динамики
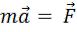 , а т.к. масса и силы не изменяются при переходе от одной системы отсчёта к другой,
, а т.к. масса и силы не изменяются при переходе от одной системы отсчёта к другой,
то равенство ускорений означает неизменность вида основного уравнения механики.
Преобразования Галилея являются математическим выражением принципа относительности Галилея(*).
(*): принципа относительности Галилея: Все инерциальные системы отсчёта в механике равноправны; это выражается в том, что законы механики во всех инерциальных системах отсчёта одинаковы. Отсюда следует, что никакими механическими опытами нельзя установить покоится, данная система или движется равномерно и прямолинейно.)
II.Угловая скорость
Угловая скорость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
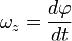 ,
,
а направлен по оси вращения согласно правилу правой руки, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду
(rad/s).
*При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах 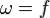 . В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так:
. В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так:  .
.
III.Связь Угловой и линейной скоростью точки
*Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью 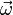 , определяется формулой:
, определяется формулой:
где 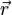 — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение.
— радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение.
Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе)  от оси вращения можно считать так:
от оси вращения можно считать так: 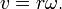 Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
IV.Переносная скорость
переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчѐта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчѐта, в данный момент времени совпадающей с материальной точкой.
V.Переносное, Центробежное и Кориолисово ускорение точки
1. Переносное ускорение
2. Центробежное ускорение
В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.
Центробежное ускорение можно вычислить по формуле: aц = V2/R

Чем больше линейная скорость тела и меньше радиус вращения, тем центробежное ускорение больше.
3. Кориолисово ускорение
При вращении диска, более далѐкие от центра точки движутся с большей касательной скоростью, чем менее далѐкие. Если мы хотим переместить некоторое тело вдоль радиуса, так, чтобы оно оставалось на радиусе, то нам придѐтся увеличить скорость тела, то есть, придать ему ускорение. Если система отсчѐта вращается вместе с диском, то мы ощутим, что тело не оставается на радиусе, а уйдет влево — это и есть сила Кориолиса.
Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной F = ma, где a — кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности. FK = − ma.
VI. зависимость ускорения свободного падения от широты местности
Чем дальше тело находится от центра Земли, тем меньше ускорение свободного падения. А она-то сплюснутая, поучается, что поверхность от центра до экватора дальше, чем аналогичное расстояние до полюса. Значит, на поюсах Земли ускорения самые большие....
2.7 ПОНЯТИЕ СИЛЫ
Сила – векторная физическая величина, в результате которой тело изменяет свою скорость или деформируется. Она характеризуется направлением, модулем и точкой приложения. Единицей измерения силы в Международной системе единиц (СИ) является ньютон (N, Н), в системе СГС — дина. Ньютон — производная единица. Она определяется как сила, изменяющая за 1с скорость тела массой 1 кг на 1 м/с в направлении действия силы. Таким образом, [1Н = 1 кг·м/с2]
СИЛЫ В ПРИРОДЕ
Всовременной физике различают четыре типа взаимодействий:
1.Гравитационное (или взаимодействие, обусловленное всемирным тяготением)
2.Электромагнитное (осуществляемое через электрические и магнитные поля)
3.Сильное или ядерное (обеспечивающее связь частиц в атомном ядре)
4.Слабое (ответственное за многие процессы распада элементарных частиц)
ФУНДАМЕНТАЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ
Фундаментальные силы - гравитационные и электромагнитные силы.
