4.3. Пример канонического метода структурного синтеза автомата

Выполним структурный синтез частичного автомата , заданного своими таблицами переходов и выходов (табл. 4.11а) и b).

Синтез будем выполнять в следующем порядке:

1. Выберем в качестве элементов памяти -триггер, функция входов которого представлена в табл. 4.5.

2. Закодируем входные, выходные сигналы и внутренние состояния автомата. Количество входных абстрактных сигналов , следовательно, количество входных структурных сигналов необходимо, т.е..

Таблица 4.11

Таблицы переходов и выходов частичного автомата

- - - -

- - - -

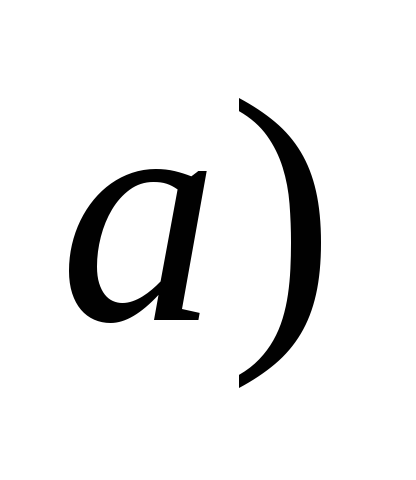
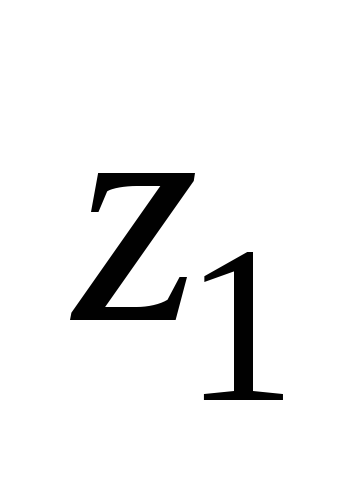
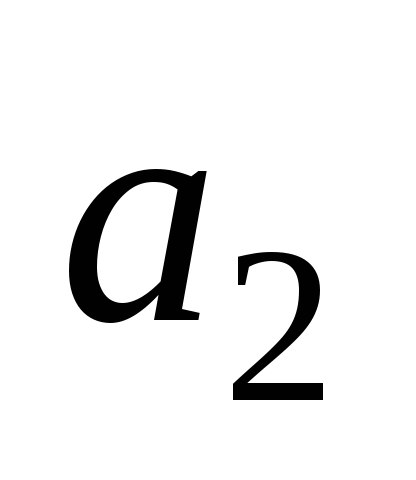
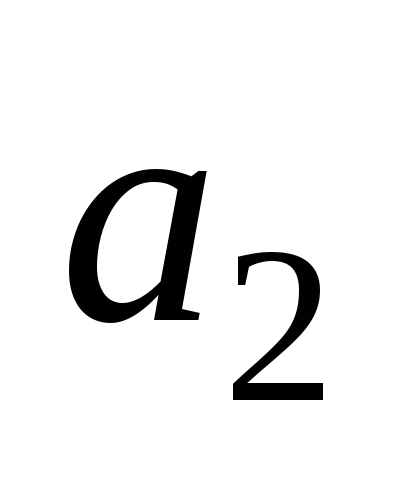
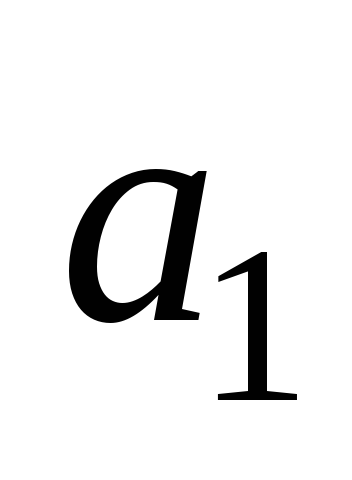
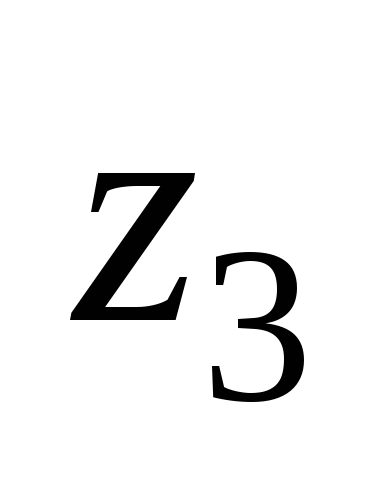
Количество выходных абстрактных сигналов , следовательно, необходимое количество выходных структурных сигналовилиу₁, у₂. Количество внутренних состояний абстрактного автомата , следовательно, необходимое количество двоичных элементов памяти (триггеров) должно быть.

Таким образом, структура ЦА с учетом того, что исходный автомат является автоматом Мили и в качестве элементов памяти используется -триггер, может быть представлена в виде (рис. 4.9):

Рис. 4.9. Структура синтезируемого ЦА

Выполним кодирование входных, выходных сигналов и внутренних состояний автомата и представим результаты кодирования в таблицах 4.12.

Таблица 4.12

Таблица кодированных входных, выходных сигналов и внутренних состояний автомата

Кодирование, в общем случае, осуществляется произвольно. Поэтому, например, каждому из сигналов можно поставить в соответствие любую двухразрядную комбинациюх₁, х₂. Необходимо только, чтобы разные выходные сигналы кодировались разными комбинациямих₁, х₂. Аналогично для и.

3. Получим кодированные таблицы переходов и выходов структурного автомата. Для этого в таблицах переходов и выходов исходного абстрактного автомата вместо сигналов ,,записываем соответствующие коды. Получим таблицы 4.13.

Таблица 4.13

Таблицы переходов и выходов структурного автомата

a)

		00	01	11	10
	00	00	10	10	-
	01		11	00	-
	11	01	-	01

b)

		00	01	11	10
	00	01	00	11	-
	01	-	11	00	-
	11	00	-	10

В кодированной таблице переходов заданы функции , а в кодированной таблице выходов приведены функции

4. При каноническом методе синтез сводится к получению функций: , а затем построение комбинационных схем, реализующих данную систему булевых функций.

Нетрудно заметить, что функции у₁ и у₂ могут быть непосредственно получены из таблицы выходов (табл. 4.13 b), например, в виде:

, .

Как обычно в теории цифровых автоматов выражения для функцийу₁ и у₂ следует упростить, и, более того, привести эти функции к минимальному виду. Для минимизации булевых функций у₁ и у₂, воспользуемся картами Карно. Тогда имеем рис. 4.10

Рис. 4.10. Минимизации булевых функций у₁ и у₂

С помощью минимизирующих карт находим

, .

(4.1)

Для получения выражений для инеобходимо получить таблицы функций возбуждения, для чего в общем случае необходимо воспользоваться таблицей переходов и функциями входов элементов памяти. Зная код исходного состояния автомата и код состояний перехода, на основании таблицы входов триггера получаем требуемое значение функции возбуждения, обеспечивающее заданный переход. ДляD-триггеров, как отмечалось ранее, таблица переходов совпадает с таблицей функции возбуждения, тогда либо непосредственно используют эту таблицу, либо в результате минимизации функций получаем требуемые значения . Обычно производится минимизация функций, как правило, с помощью карт Карно. Карты Карно приведены на рис. 4.11

	00	01	11	10
00	0	1	1	-
01	-	1	0	-
11	0	-	0	1
10	-	-	-	-

	00	01	11	10
00	0	0	0	-
01	-	1	0	-
11	1	-	1	1
10	-	-	-	-

Рис. 4.11. Минимизация функций возбуждения

В результате минимизации получили

, .

(4.2)

5. На основании полученных в результате синтеза булевых выражений (4.1), (4.2), можно создать функциональную схему автомата, но для этого уравнения (4.1), (4.2) перепишем так ,,,.