3.3. Графический способ задания автомата

Граф автомата - это ориентированный связный граф, вершины которого соответствуют состояниям, а ребра графа – переходам между ними. Две вершины графа автомата соединяются ребром, направление указывается стрелкой. Ребру графа приписывают соответствующие значения входных и выходных сигналов, если они определены. Если переход из состояния в состоянияпроисходит под воздействием нескольких входных сигналов, то соответствующему ребруприсваивают все значения входных и выходных сигналов.

Е

сли с помощью графа-схемы описывают автомат Мура, то выходной сигналзаписывается либо в вершине графа, либо около нее. На рис 3.2 изображены граф автомата Мили, а на рисунке 3.3 - граф автомата Мура, исходя из табл. 3.9 и 3.10

Таким образом, разметку ребер и состояний следует выполнять, руководствуясь следующими правилами. Ребро графа направленное из вершины в вершину, определяет переход автомата из состоянияв состояние.

Рис. 3.2. Граф-схема автомата Мили

Вначале этого ребра следует записать входной сигнал, вызывающий этот переход из состоянияв состояние.

Р

ис. 3.3 Граф-схема автомата Мура

Для автомата Мили, выходной сигнал , формируемый при переходе из состоянияв состояние, записывается в конце ребра графа, а для автомата Мура рядом с вершиной.

3.4. Матричный способ задания автомата

Абстрактный автомат также может быть задан с помощью матрицы соединений автомата – квадратной матрицей , строки которой соответствуют начальным внутренним состояниям, а столбцы состояниям в момент. Элемент, который находится на пересечении-ой строки и-го столбца, для автомата Мили соответствует входному сигналу, который обеспечивает переход автомата из состоянияв состояниеи выходному сигналу, который при этом формируется. Так, для автомата Мили, заданного табл. 3.9, матрица соединений имеет вид

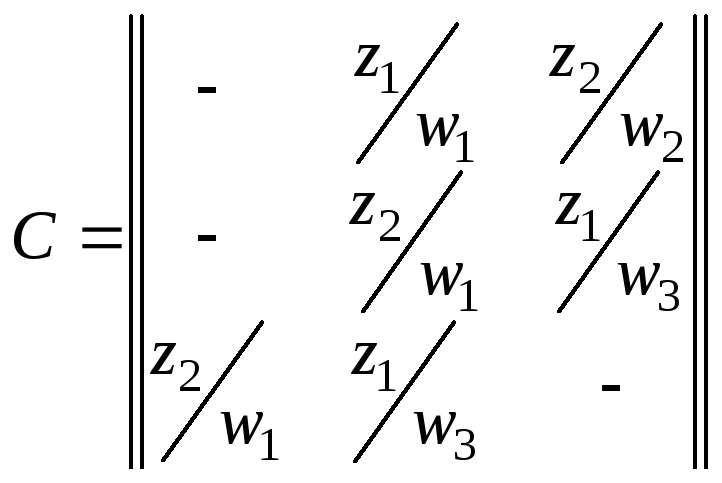
Если переход из состояния в состояниепроисходит вследствие действия нескольких сигналов, то элемент матрицыпредставляет собой множество пар вход/выход для этого перехода, который соединяется символом дизъюнкции.

При матричном задании автомата Мура элемент равен множеству входных сигналов на переходе, а выход записывается в виде соответствующей матрицы. Так, для автомата Мура заданного таблицей 3.10, имеем

_.

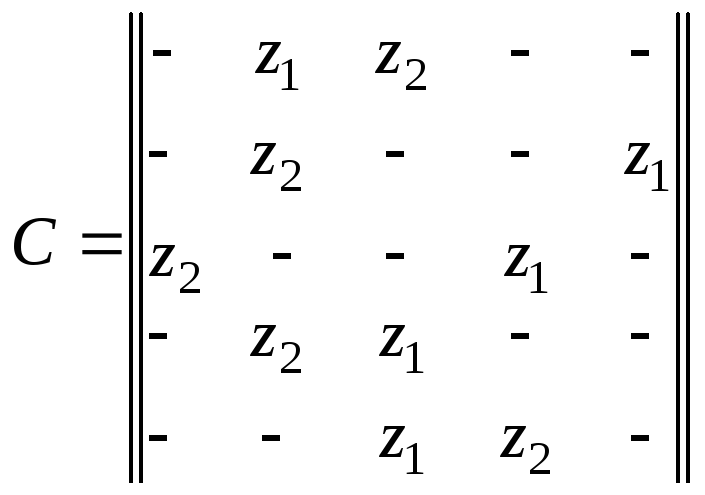
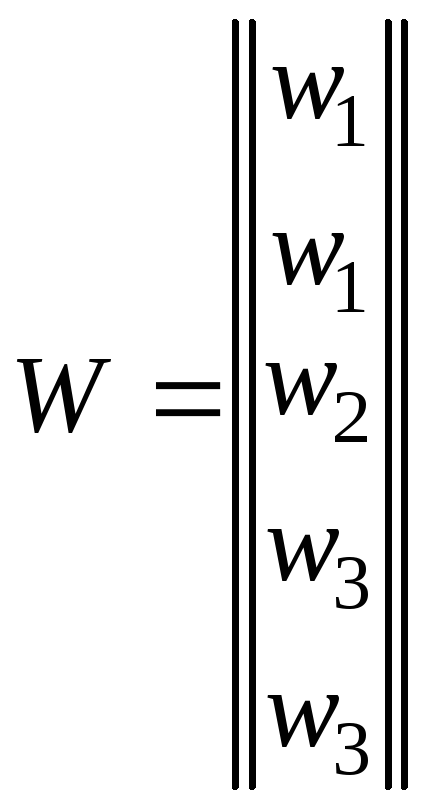3.5. Эквивалентность автоматов

Определение. Два автомата ис одинаковыми входными и выходными алфавитами называютсяэквивалентными, если после установки их в начальные состояния реакции этих автоматов на любое входное слово совпадают.

Другими словами, при подаче на вход эквивалентных автоматов, находящихся в одинаковом состоянии, одних и тех же слов, их выходные слова также должны быть одинаковыми. Оказывается, что для любого автомата Мили существует эквивалентный ему автомат Мура, и, обратно, для любого автомата Мура существует эквивалентный ему автомат Мили. Рассматривая алгоритм взаимной трансформации этих автоматов, будем пренебрегать выходным _{сигналом, который связан с начальным внутренним состоянием в обоих автоматах.}

_{Рассмотрим процедуру трансформации конечного автомата Мура в эквивалентный ему автомат Мили. Предположим, что начальный автомат Мура, задан множеством входных, выходных сигналов и множеством состояний, и функциями выхода и перехода} . Требуется построить эквивалентный автомату Мили автомат Мура. Для этого необходимо обеспечить выполнение следующих условий:

, ,и.

Эквивалентность функций выходов автоматов определяется так: если для автомата Мура имеем функции переходов и его функция выходов, то и в автомате Мили функция выходов должна формировать выходной сигнал.

Переход от автомата Мура , когда он задан таблично, к автомату Милив случае совпадения таблиц переходов, производится посредством замены состояния, находящегося на пересечении столбцаи строкив таблице переходов на обозначение выходного сигнала, а именно, для автомата Мили. Последовательно выполняя указанную процедуру замен, получаем совмещенную таблицу переходов и выходов автомата Мили. Из принципа построения автомата Милиочевидна его эквивалентность начальному автомату Мура.

Действительно, если входной сигнал поступит на вход автомата Мура, который находится в состоянии, то он перейдет в состояниес соответствующим выходным сигналом. Заметим, что эквивалентный ему автомат Мили из состояниятакже перейдет в состояние, вырабатывая при этом выходной сигнал.

Трансформация автомата Мили в эквивалентный автомат Мура производится по следующему правилу: реализация каждого состояния , переход в который сопровождается формированием различных выходных сигналов, производится с помощью совокупности состояний,,,, каждому из которых соответствует только выходной сигнал. В обозначенной таблице переходов и выходов автомата Мура фиксируются новые состояния. Очевидно, количество внутренних состояний автомата Мура будет большим, чем количество состояний эквивалентного ему автомата Мили.

Пример. Для автомата Мили, заданного таблицей 3.11, построить обозначенную таблицу переходов и выходов эквивалентного автомата Мура

В соответствии с приведенным правилом и используя таблицу 3.11, запишем множество пар «состояние-выход» для автомата Мура и пронумеруем те пары, которые порождены каждым состоянием автомата Мили: ;;.

С каждым состоянием автомата Мура связывают выходной сигнал , который является вторым элементом пары. Тогда

; ;.

Учитывая эти обозначения, получаем таблицу 3.12, получаем обозначенную таблицу переходов и выходов эквивалентного автомата Мура.

Таблица 3.12

Обозначенная таблица переходов и выходов эквивалентного автомата Мура

Таблица 3.11

Таблица переходов и выходов эквивалентного автомата Мили

Таким образом, в результате выполненных операций получена обозначенная таблица переходов и выходов эквивалентного автомата Мура. На этом примере видно, что количество состояний эквивалентного автомата Мура увеличилось в сравнении с количеством состояний автомата Мили. Переход от автомата Мили к эквивалентному автомату Мура не приводит к изменению количества состояний.