3.2. Табличное задание автоматов Мили и Мура

При табличном способе задания автомат Мили описывается с помощью двух таблиц: одна из них – таблица переходов, отражает действие функции , т.е.(см. табл. 3.1), а вторая таблица – таблица выходов автомата Мили соответствует функциии составляется по уравнению(табл. 3.2). К

Таблица 3.1

Таблица переходов автомата Мили

аждому столбцу из приведенных таблиц 3.1, 3.2 поставлен в соответствие один входной сигнал из множества состояний, а каждой строке – одно внутреннее состояние из множества состояний. На пересечении столбцаи строкив таблицы переходов записывается состояние, в которое должен перейти автомат из состоянияпод действием входного сигнала, где. Аналогично, в таблицу переходов на пересечении-го столбца и-ой строки таблицы выходов записывается выходной сигнал, выдаваемый автоматом в состояниипри поступлении на его вход сигнала, т.е..

Tаблица 3.2

Таблица выходов автомата Мили

Задание таблиц переходов и выходов полностью описывает работу конечного автомата, поскольку задаются не только сами функции переходов и выходов, но также и все три алфавита: входной, выходной и алфавит состояний.

Используя приведенные таблицы переходов и выходов, образующие автомат Мили ,иможно задать этот автомат одной совмещенной таблицей переходов и выходов (табл. 3.3), в которой каждый элемент таблицы записывается в виде. Составим совмещенную таблицу переходов и выходов автомата Мили исходя из таблиц 3.1, 3.2.

Автомат Мура задается одной отмеченной таблицей переходов (табл. 3.4), поскольку в этом автомате выходной сигнал однозначно определяется состоянием автомата. Поэтому каждому столбцу автомата Мура присвоены не только состояния , но еще и выходной сигналсоответствующий каждому состоянию, определяемый по формуле.

Таблица 3.3

Совмещенная таблица переходов и выходов автомата Мили

Таблица 3.4

Отмеченная таблица переходов автомата Мили

			…
			…
…	…	…	…	…
			…

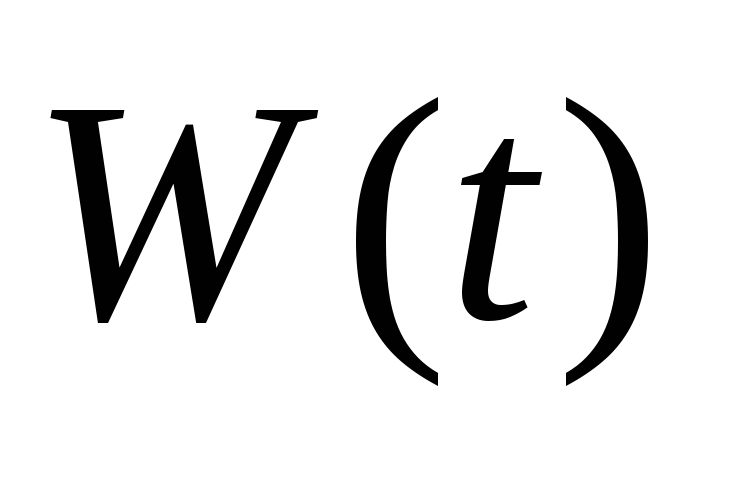
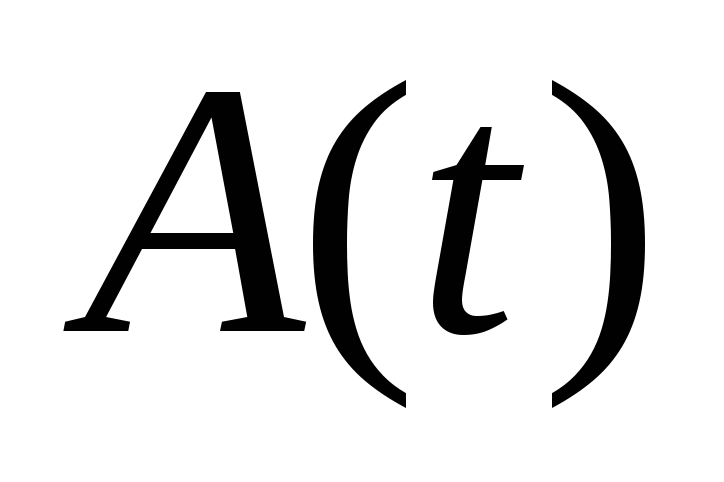
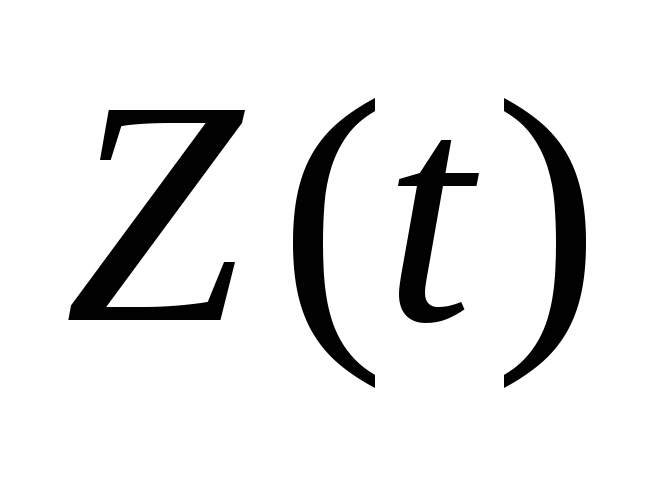
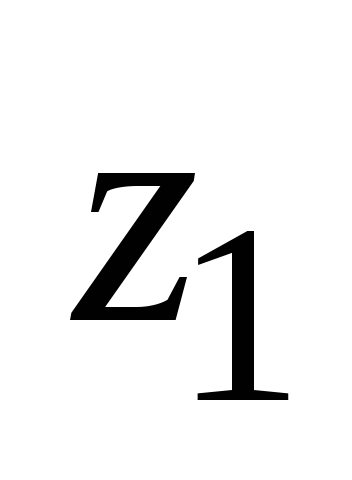
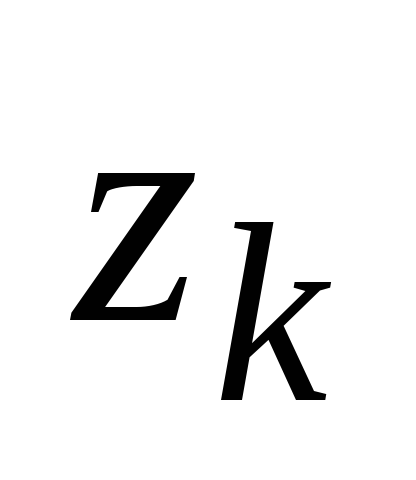
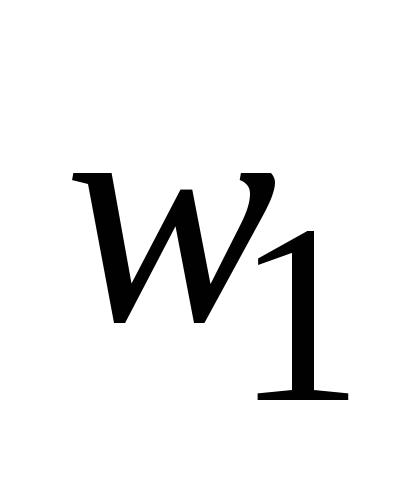
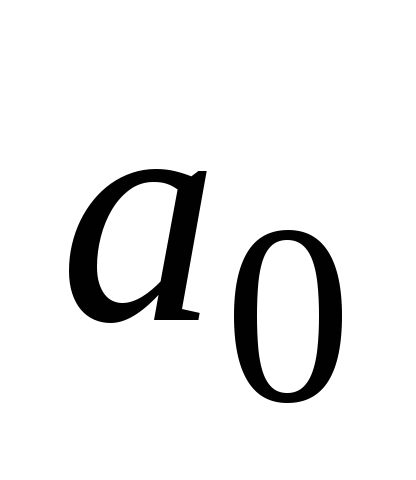
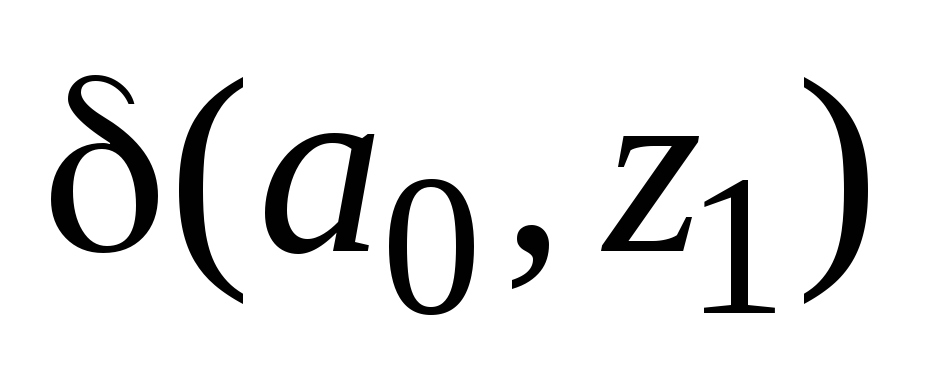
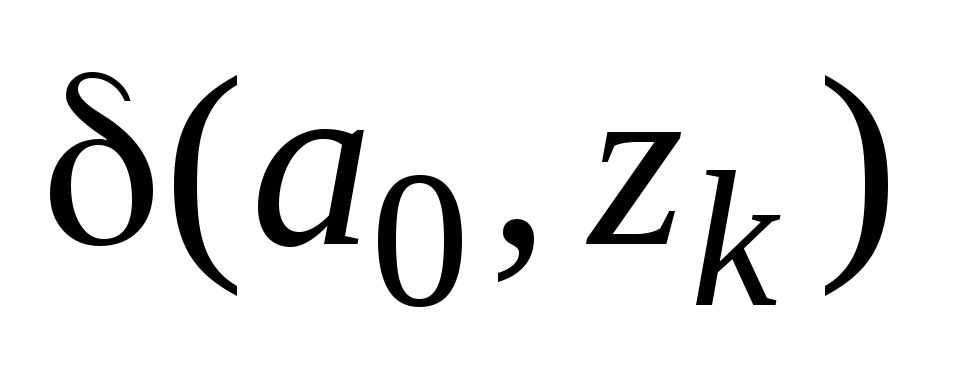
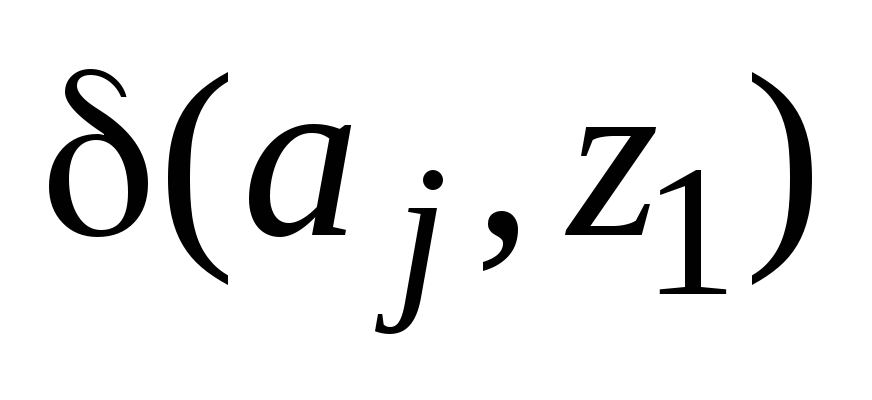
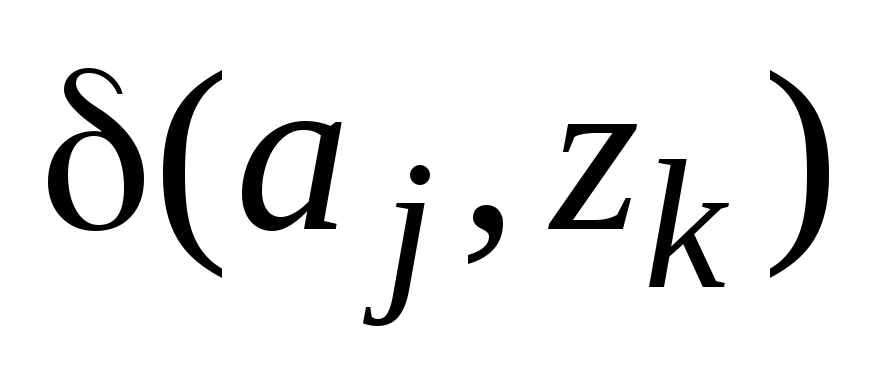
Таблицу переходов автомата Мура называют отмеченной, потому что каждое состояние отмечено еще и выходным сигналом.

В инженерной практике часто встречаются автоматы, на входы которых некоторые последовательности сигналов никогда не подаются. Такие последовательности называют запрещенными входными словами данного автомата, а сам автомат – частичным автоматом. У частичного автомата функции переходов и выходов определены не для всех пар ,. На месте неопределенных состояний и выходных сигналов ставится прочерк. При синтезе схем обычно выполняют доопределение частичного автомата до полного автомата, так чтобы его схемная реализация получилась как можно проще.

Кроме автоматов Мили и Мура иногда оказывается удобным пользоваться совмещенной моделью автомата, так называемым – автоматом. Под абстрактным– автоматом будем понимать математическую модель дискретного устройства, определяемую восьмикомпонентным вектором, у которого:– множество состояний;– входной алфавит;– выходной алфавит типа 1, а–-я буква выходного алфавита, определяется соотношением;– выходной алфавит типа 2, а–-я буква выходного алфавита, определяется соотношением;– функция переходов;– функция выходов типа 1;– функция выходов типа 2;начальное состояние автомата. Абстрактный– автомат можно представить как устройство с одним входом, на которое поступают сигналы из входного алфавита, и двумя выходами, на которых появляются сигналы из алфавитови. Отличие– автомата от моделей Мили и Мура состоит в том, что он одновременно реализует две функции выходов₁ и ₂, каждая из которых может быть реализована автоматом Мили и Мура в отдельности. Закон функционирования – автомата можно описать следующими уравнениями:

,

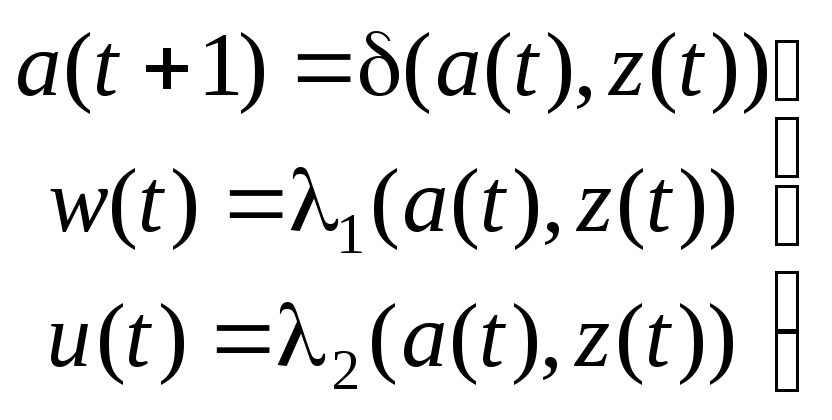где ..

Для задания – автоматов также используется табличный метод. В этом случае можно построить, так же как и для автомата Мили, таблицу переходов (табл. 3.5) и таблицу выходов (табл. 3.6). Таблица переходов аналогична таблице переходов автомата Мили, а в таблице выходов содержится дополнительные столбцы, соответствующие выходному алфавиту(см. табл. 3.6).

Пример табличного описания полностью определённого цифрового автомата Мили S₁ с тремя состояниями, двумя входными и двумя выходными сигналами приведён в таблицах 3.7 и 3.8 и совмещенная таблица переходов и выходов автомата Мили (табл. 3.9).

Таблица 3.5

Таблица переходов С - автомата

Пример табличного описания полностью определённого цифрового автомата Мили S₁ с тремя состояниями, двумя входными и двумя выходными сигналами приведён в таблицах 3.7 и 3.8 и совмещенная таблица переходов и выходов автомата Мили (табл. 3.9).

Таблица 3.6

Таблица выходов C – автомата

Таблица 3.7 Таблица переходов автомата Мили					Таблица 3.8 Таблица выходов автомата Мили

Поскольку в автомате Мура выходной сигнал формально является функцией внутреннего состояния, то он задается одной так называемой обозначенной таблицей переходов и выходов, у которой в каждой строке добавляется кроме состояния еще и выходной сигнал, соответствующий этому состоянию.

Таблица 3.10

Обозначенная таблица переходов и выходов автомата Мура

Таблица 3.9

Совмещенная таблица переходов и выходов автомата Мили

Как отмечалось выше, функционирование цифрового автомата можно представить графически. Рассмотрим ниже графический способ представления законов функционирования автоматов.