Лекция 8 сложное движение точки

Рассмотрим движение точки М относительно двух систем координат Oxyz и O₁x₁y₁z₁, движущихся друг относительно друга (рис. 8.1). В механике системы координат предполагаются жестко скрепленными с телами, по отношению к которым рассматривается движение точки. Тела на рисунках можно не показывать.

Рис. 8.1

Пусть задано движение системы координат Oxyz относительно системы координат O₁x₁y₁z₁. Движение точки М относительно системы координат O₁x₁y₁z₁ называют сложным, если задано ее движение относительно системы координат Oxyz. Систему координат O₁x₁y₁z₁ принимают при этом за неподвижную или основную, а систему координат Oxyz - за подвижную.

Относительное движение

Движение точки М относительно подвижной системы координат называют относительным. Соответственно, траектория (рис. 8.1), скорость и ускорение точки в ее движении относительно подвижной системы координат называются относительными. Относительная скорость и относительное ускорение точки обозначается индексом r: ,. Положение точкиМ по отношению к системе координат Oxyz определяет радиус-вектор .

Введем орты подвижной системы координат и разложим радиус-вектор по ортам

.

Уравнения

, ,(8.1)

являются уравнениями относительного движения точки в координатной форме. Движение самой координатной системы Oxyz не учитывается, считаем ее неподвижной.

Если в уравнениях (8.1) исключить время, то получим уравнения траектории относительного движения (рис. 8.1).

Если относительное движение задано, то для того, чтобы найти относительную скорость точки , необходимо продифференцировать вектор-функциюв предположении, что ортынеподвижны.

. (8.1а)

Знак ~ (тильда) в равенстве (8.1а) означает, что производная берется в предположении, что - постоянные векторы. Такая производная называется локальной или относительной производной.

Раскладывая вектор по ортам

и сравнивая две записи вектора , имеем

, ,.

Аналогично ускорение относительного движения точки равно:

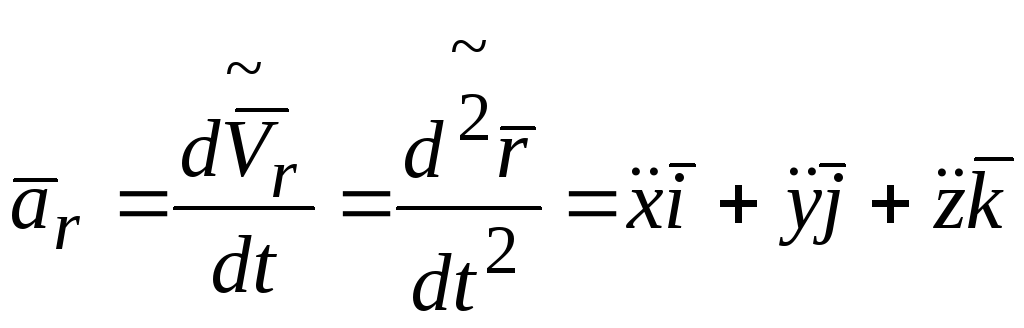. (8.2)

Раскладывая вектор по ортам

и сравнивая обе записи вектора , имеем

, ,.

Следовательно, для определения относительной скорости и относительного ускорения точки следует мысленно остановить движение подвижной системы координат и вычислить их по правилам кинематики точки.

Абсолютное движение точки

Движение точки М относительно неподвижной системы координат называют абсолютным. Соответственно, траекторию (рис. 8.1), скорость и ускорение относительно неподвижной системы координат называют абсолютными.

Абсолютная скорость и абсолютное ускорение точки обозначается индексом а:,. Положение точкиМ относительно неподвижной системы координат O₁x₁y₁z₁ определяется радиус-вектором . Введем орты неподвижной системы координати разложим по ним радиус-вектор:

.

Тогда уравнения абсолютного движения точки имеют вид

, ,. (8.3)

Исключив в уравнениях (8.3) время , получим уравнения траектории абсолютного движения точки (рис.8.1).

Чтобы найти скорость абсолютного движения точки, необходимо продифференцировать вектор-функцию :

.

Раскладывая вектор по ортам

и, сравнивая обе записи вектора , получим

, ,.

Аналогично, ускорение абсолютного движения точки равно:

.

Раскладывая вектор по ортам

и сравнивая обе записи вектора , получим

, ,.