FTF 1 semestr.MAVRODI / 64
.pdf
Определенным интегралом от a до b непрерывной функции y=f(x), определенной на интервале 
a;b
, называется приращение первообразной F(x) для этой функции,
то есть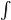 
baf(x)dx=F(b)−F(a)=F(x)
ba .
Числа a и b называются нижним и верхним пределами интегрирования.
Основные правила и свойства определенного интеграла
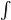baf(x)dx=
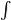baf(t)dt
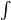aaf(x)dx=0
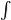baCf(x)dx=C
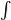baf(x)dx
baf(x)dx=−
abf(x)dx
baf(kx+l)dx=k1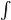
kb+lka+lf(t)dt
ba
f(x)
g(x)
dx=
baf(x)dx
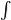bag(x)dx
baf(x)dx=
caf(x)dx+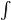
bcf(x)dx
Физический смысл определенного интеграла:
Путь S, пройденный телом при прямолинейном движении со скоростью v(t) за интервал времени от t1 до t2, вычисляется по формуле
S=
t2t1v(t)dt
Геометрический смысл определенного интеграла:
Площать S криволинейной трапеции (фируры, ограниченной графиком непрерывной положительной на интервале 
a;b
функции y=f(x), осью OX и прямыми x = a и x = b) вычисляется по формуле
S=
baf(x)dx
Необходимое условие существования определенного интеграла Если функция интегрируема (по Риману) на отрезке, то она ограничена на нем.
Доказательство. Пусть |
интегрируема на |
, т.е. существует |
. Покажем ограниченность |
||
функции |
на |
, т.е. |
|
|
|
.
Предположим, что 
не ограничена на 
. Тогда
.
При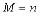 
, 
можно построить последовательность 
: 
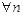
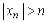и 
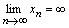. Поэтому можно указать такое
разбиение 
отрезка 
и провести выбор чисел 
так, что интегральная сумма примет значение больше любого наперед заданного числа, т.е. определение определенного интеграла не выполнится.
Итак, только для ограниченной на 
функции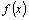 
существует интеграл .
Заметим, однако, что не для всякой ограниченной на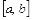 
функции 
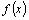существует интеграл, т.е. требование ограниченности функции является НЕОБХОДИМЫМ, но не является ДОСТАТОЧНЫМ условием интегрируемости функции.
Контрпример. Пусть |
|
|
|
|
|
|
Тогда для всякого разбиения на |
можно указать систему точек |
такую, что |
|
и |
||
поэтому |
, а также |
|
, т.е. |
. При |
не существует единого |
|
предела для интегральной суммы, не зависящего от |
|
|
|
|
||
и , т.е. функция |
, будучи ограниченной на |
, не является интегрируемой (по Риману) на |
. |
|||
Аналогичные соображения имеют место и для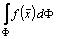 
в общем случае:
если интеграл |
, построенный соответственно рассмотренной выше процедуре (по Риману), существует, |
|||
то |
– |
|
|
|
ограниченная на |
функция, т.е. только для ограниченных на функций |
, |
, можно рассматривать |
|
указанный интеграл. |
|
|
|
|
Необходимые и достаточные условия существования интеграла Римана подробно изложены, например, в [1].
Сформулируем некоторые ДОСТАТОЧНЫЕ условия существования определенного интеграла, т.е. укажем классы функций 
, 
, интегрируемых по Риману: если
либо 1)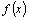 
– непрерывна на 
,
либо 2) 
– кусочно-непрерывна и ограничена на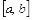 
;
либо 3) 
– монотонная или кусочно-монотонная и ограничена на 
, то определенный
интеграл |
существует (имеет конечное значение). |
Впредь будем предполагать, что все рассматриваемые функции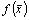 
и множества 
, 
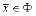, обладают ("хорошими")
свойствами, нужными для существования интеграла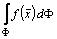 
.