FTF 1 semestr.MAVRODI / 61
.pdf
Рассмотрим случаи, когда заменой переменной можно свести интегрирование нерациональных функций к интегрированию рациональных функций (т. е., как говорят, рационализировать интеграл).
Пусть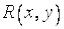 
- рациональная функция своих аргументов 
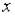и 
, т. е. над 
и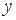 
совершаются только арифметические операции, чтобы получить 
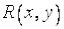. Например,
|
|
- рациональная функция, а |
|
|
|
|
- не является рациональной. |
|
|
I. В ы ч и с л и т ь |
|
, где |
- постоянные числа, -натуральное |
|
число, |
, |
- рациональная функция. |
|
|
Функцию вида |
|
называют дробно-линейной иррациональностью. |
|
|
Покажем, что замена |
рационализирует интеграл. В самом деле, |
, |
||
откуда |
- рациональная функция от |
. Далее, |
|
|
.
Поэтому
,
где 
- рациональная функция по 
, интегрировать которую мы умеем.
П р и м е р 1. Вычислить |
|
. Здесь |
. Полагая |
, |
|
получим |
, |
, |
. Таким образом, |
|
|
.
П р и м е р 2.
|
|
. |
|
II. Вычислить |
, где |
- постоянные числа. |
|
Функцию |
будем называть квадратичной иррациональностью. |
||
Если трехчлен |
имеет действительные корни , |
, |
|
то |
и |
|
|
и дело сводится к случаю 1.
Поэтому будем считать, что 
не имеет действительных корней и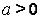 
. Тогда рационализация интеграла может быть достигнута с помощью подстановки Эйлера:
|
. |
|
Отсюда |
, т. е. |
- рациональная функция от . Но тогда |
- также рациональная функция от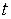 
. Поэтому
.
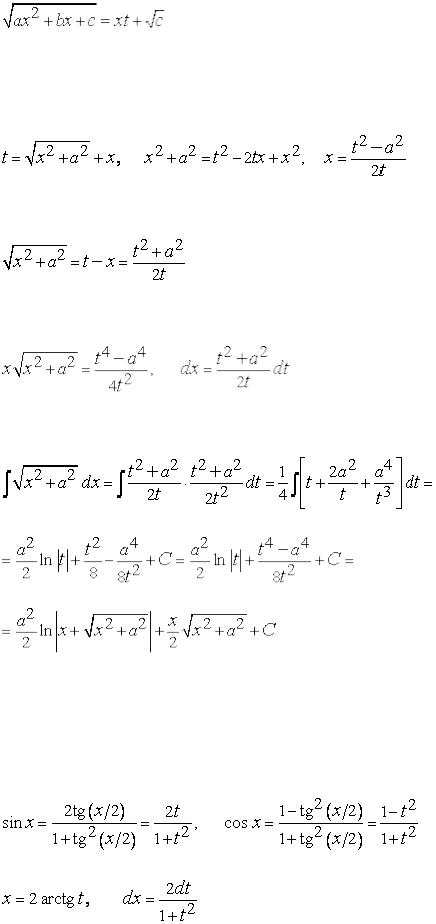
З а м е ч а н и е. Если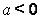 
, а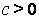 
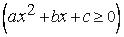, то можно сделать замену
.
П р и м е р 3. Вычислить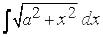 
. Бином 
не имеет действительных корней. Поэтому полагаем
и
.
Отсюда
.
В силу этого
.
III. И н т е г р и р о в а н и е в ы р а ж е н и й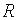 
.
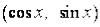Рационализация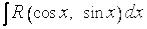 
достигается с помощью подстановки 
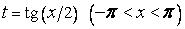, которая называется универсальной. В самом деле
,
,
поэтому
.
Если функция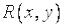 
обладает свойствами четности или нечетности по переменным 
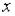или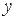 
, то могут употребляться и другие подстановки, также рационализирующие интеграл.
Пусть
,
где 
и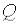 
- многочлены от 
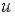и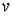 
.
1)Если один из многочленов 
, 
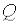четный по 
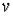, а другой – нечетный по 
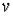, то подстановка 
рационализирует интеграл.
2)Если один из многочленов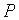 
, 
четный по 
, а другой – нечетный по 
, то подстановка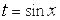 
рационализирует интеграл.
3)Есл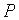и 
и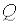 
: а) оба не изменяются при замене 
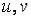соответственно на 
или б) оба меняют знак, то интеграл рационализируется подстановкой 
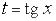(или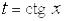 
).
П р и м е р ы:
. |
. |
. |
. |
В данном случае , т. е. числитель нечетный относительно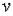 
, а знаменатель четный по 
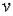, и мы имеем дело со случаем 
.
.
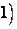Здесь числитель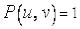 
, а знаменатель 
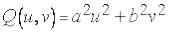. Оба не меняются при замене 
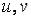соответственно на 
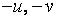, т. е. мы имеем дело со случаем 
.
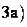Эйлера подстановки подстановки, служащие для приведения интегралов вида
где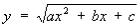 
R (x, y) — рациональная функция от х и у, к интегралам от рациональных. Предложены Л. Эйлером.
применима, если а>0;
применима, если с > 0;
где λ — один из корней трёхчлена ax2 + bx + c, применима, если корни этого трёхчлена действительны. На практике Э. п. требуют громоздких преобразований и потому вместо них обычно пользуются теми или иными искусств. приёмами, упрощающими вычисление.
Аналогичные подстановки делаются в теории чисел при решении неопределённых уравнений 2-й степени в рациональных числах.