FTF 1 semestr.MAVRODI / 57
.pdf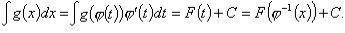
Замена переменных в неопределенном интеграле
1. 
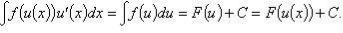
2. Если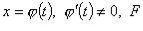 
- первообразная для 
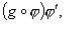то
Замена переменной в неопределённом интеграле (интегрирование подстановкой).
Пусть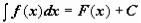 
. Тогда 
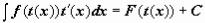. Здесь t(x) - дифференцируемая монотонная функция.
Док-во непосредственно следует из формулы для производной сложной функции. Перепишем первый интеграл, заменив переменную x на t: 
. Это означает, что 
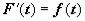. Заменим независимую переменную t на
функцию t = t(x):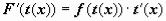 
. Следовательно, функция F(t(x)) является первообразной для произведения 
, или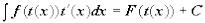 
.
При решении задач замену переменной можно выполнить двумя способами.
1. Если в подынтегральной функции удаётся сразу заметить оба сомножителя,
и f(t(x)), и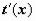 
, то замена переменной осуществляется подведением множителя 
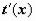под знак дифференциала: 
, и задача сводится к вычислению интеграла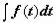 
.
Например,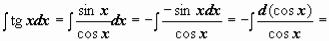 
(задача сведена к вычислению 
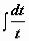, где t = cos x) 
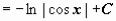(аналогично находится интеграл от 
); 
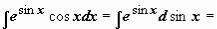(задача сведена к вычислению 
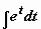, где t =
sin x)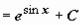 
. В более сложных задачах операция подведения под знак дифференциала
может выполняться несколько раз: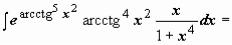 
(самое неприятное в подынтегральной функции - пятая степень арккотангенса под знаком экспоненты; если дальше не найдётся дифференциал этой функции, то интеграл, возможно, взять вообще не удастся; в то же время следующий множитель (arcctg4 x2) - производная (с точностью до постоянного множителя) степенной функции; затем следуют производные (опять с точностью до постоянных множителей) функций arcctg x2 и x2 по своим
аргументам)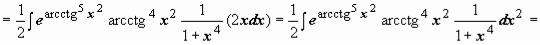 
.
2. Замену переменной можно осуществлять формальным сведением
подынтегрального выражения к новой переменной. Так, в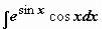 
имеет смысл перейти к переменной (сделать подстановку) t = sin x. Выражаем все множители подынтегрального выражения через
переменную t: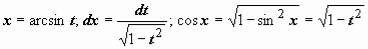 
; в
результате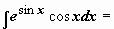 
(возвращаемся к исходной переменной) 
. Другие примеры:
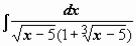. Подынтегральная функция содержит два множителя, ни один из которых не является производной другого, поэтому подводить их под знак дифференциала бесполезно. Попытаемся ввести новую переменную, такую, чтобы корни
извлеклись: |
= |
. 
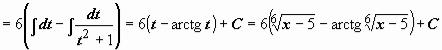Рассмотрим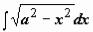 
(интеграл №19 из табл. 10.3.неопределённых интегралов).
Здесь подынтегральная функция состоит из единственного множителя; можно опять попытаться сделать такую замену переменной, чтобы корень извлёкся. Структура подкоренного выражения подсказывает эту замену: 
(или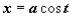 
, 
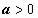
): . Интеграл свёлся к интегралу от квадрата косинуса. При интегрировании чётных степеней синуса и косинуса часто
применяются формулы, выражающие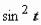 
и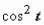 
через косинус двойного угла: 
. 
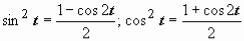Поэтому
.
Искусство интегрирования в основном заключается в умении видеть необходимые подстановки; оно, как и любое другое искусство, вырабатывается упражнениями. Для основных классов функций требуемые подстановки будут изучаться дальше, здесь мы покажем, с помощью каких преобразований были выведены формулы 17, 15, 20 Таблицы
10.3.неопределённых интегралов:
17.
.
15.
.
20.
. Второй интеграл элементарно сводится к
первому: |
. |