Курс лекций Оптическая физика

81

Преобразуем r к другому виду. Сначала умножим разные слагаемые числителя и знаменателя на разные части равен-

Френеля для амплитудных коэффициентов отражения и преломления для поляризации света перпендикулярной плоскости падения.

Угол Брюстера

света на границу раздела двух сред, — угол преломления.

этот результат с другим выражением для коэффициента отражения

r|| n2 cos 1 n1 cos 2 n2 cos 1 n1 cos 2

получаем n2 cos 1 n1 cos 2 0.

Окончательно получаем, что для угла падения такого,

что tg n2 , в отраженном свете нет поляризации парал- n1

82

лельной плоскости падения света || 0. Такой угол падения

света называется углом Брюстера, а уравнение tg n2 n1

удобно для вычисления угла Брюстера.

Прохождение света без потерь на отражение используется в лазерах с малым усилением активной среды. Так усиливающая свет лазерная среда в газовых лазерах обычно помещается в разрядную трубку с брюстеровскими окнами. Брюстеровские окна — прозрачные плоскопараллельные пластины, расположенные под углом Брюстера к оптической оси лазера.

Коэффициент отражения и пропускания по энергии.

Обычно под коэффициентами отражения и пропускания понимают не амплитудные коэффициенты

E , а энергетические коэффициенты.E

I r

R (8.11) — коэффициент отражения или отража-

I i

тельная способность.

T I cos 2 (8.12) — коэффициент пропускания или

I i cos 1

пропускательная способность.

R T 1 (8.13) — вся падающая на границу раздела сред энергия или отражается или проходит насквозь.

Обсудим, почему в определении энергетического коэффициента пропускания присутствует отношение косинусов угла преломления и угла падения света.

83

Рис. 8.3. Иллюстрация разницы ширины отраженного и преломленного лучей.

Оказывается, что при наклонном падении света на границу раздела сред I i I r I .

Рассмотрим пучок лучей конечной ширины.

Из рис. 8.3 видно, что ширина преломленного пучка BD отличается от ширины AC падающего пучка лучей.

Интенсивность света — это энергия, падающая в единицу времени на площадку единичной площади перпендикулярную лучу. Изменение площади сечения пучка и приводит к неравенству I i I r I .

Если же рассмотреть энергию, падающую на единицу площади границы раздела сред, то для этой энергии падающая энергия равна сумме отраженной и преломленной.

Площадь пучка на границе раздела сред отличается от площади поперечного сечения пучка в косинус раз

ницу времени через единицу площади границы раздела сред, имеет сомножитель в виде косинуса: I cos . Найдем связь амплитудных и энергетических коэффициентов отражения и пропускания. Интенсивность света I связана с вещественной E0 или комплексной E0 амплитудой света соотношением:

R r 2 — связь энергетического и амплитудного коэффициен-

тов отражения.

Исключая случай полного внутреннего отражения, который мы рассмотрим позднее, амплитудный коэффициент отра-

жения от прозрачной среды всегда вещественен. ТогдаR r2 . В случае полного внутреннего отражения света энерге-

тический коэффициент отражения равен единице R 1. Отраженная световая волна при этом сдвинута по фазе относительно падающей волны. По этой причине амплитудный коэффициент

85

Кроме косинусов связь энергетического и амплитудного коэффициентов пропускания содержит отношение показателей преломления двух сред. Это связано с различной фазовой скоростью света в двух средах.

очень удачным выбором положительного направления вектора

E отраженной волны для поляризации параллельной плоскости падения света. Для любой поляризации света в отраженной при

нормальном падении света волне вектор E направлен навстречу

вектору E падающей волны.

Пусть отраженная волна имеет отрицательную амплиту-

ду, но 1 ei , следовательно, можно сказать, что отраженная волна сдвинута по фазе на . Сдвиг фазы эквивалентен раз-

ности хода , поэтому и говорят, что при отражении от оптиче-

2

ски более плотной среды происходит потеря полуволны.

86

Лекция 9

Полное внутреннее отражение света Отражение света от поверхности металла

Оптические постоянные металлов и их определение

Условие возникновения полного внутреннего отра-

жения.

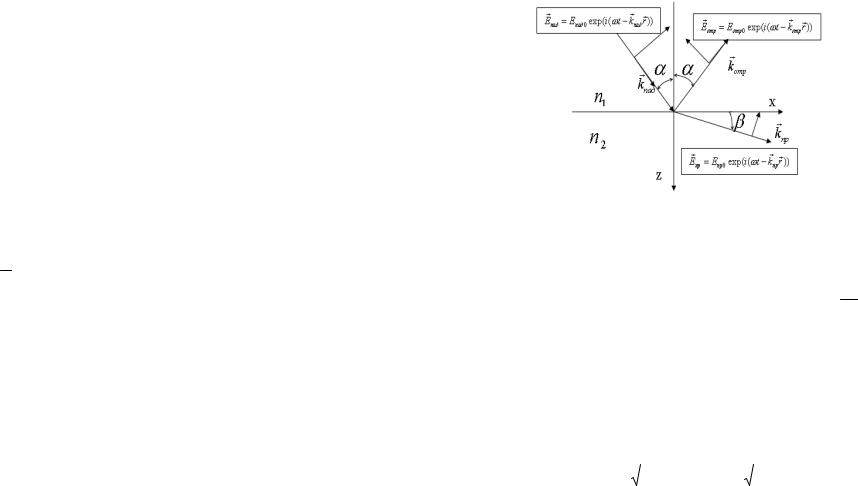
Рис. 9.1. Структура отраженной и преломленной волн. Пусть свет падает из среды с большим показателем пре-

ломления на границу среды с меньшим показателем преломления: n1 n2 . Закон преломления n1 sin n2 sin выполняется

до граничного значения угла падения 0 arcsin n2 . Это n1

предельный угол полного внутреннего отражения. Этот угол

87

При подкоренное выражение положительно. Волновой вектор прошедшей (преломленной) волны будет комплексным, и прошедшая волна примет вид:

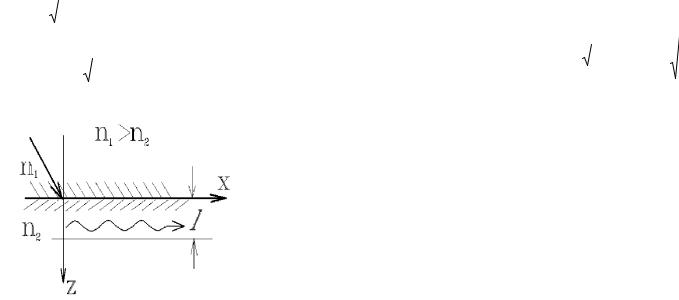
никновения света во вторую среду при полном внутреннем от-

ражении. Она очень мала: 10 6 м

Рис. 9.2. Перенос энергии при полном внутреннем отра-

жении.

на. Для нее плоскости постоянной фазы: x constперемещаются вдоль границы раздела плоскости постоянной амплитуды:

нос энергии в узком приповерхностном слое. Выясним теперь что происходит с отраженной волной при 0 . Для отра-

женного света коэффициент отражения

квадраты амплитуды надо вычислять как квадраты модулей комплексных чисел).

ствие неоднородной прошедшей волны, вся энергия падающего света отражается полностью.

Полученный результат - для установившегося режима, а в момент установления равновесия на границе, т.е. в первый момент падения волнового фронта малая часть энергии прони-

кает во вторую среду и переносится в узком слое толщины .

Явление полного внутреннего отражения используется для поворота луча на 90°, для переворачивания изображения, в рефрактометрах для определения показателя преломления жидкости, в счетоводах, волоконной оптике, ЭВМ.

Отражение света от поверхности металла. Оптические постоянные металлов и их определение

Так как уравнения Максвелла и граничные условия справедливы для любых сред, то на границе диэлектрик-металл (т.е. при падении света на плоскую поверхность металла) должны выполняться тс же формулы Френеля.

Но есть существенное отличие: в металле (проводнике)

существует огромное число свободных электронов

(n 1022 см 3) . Падающая волна заставляет их двигаться с ускорением

89

Рис. Взаимодействие электромагнитной волны с метал-

лом.

a eEпад в противофазе. m

Поэтому и вторичные волны, испущенные такими элек-

тронами, колеблются в противофазе с падающей:

easin Eвт 4 0с2r

Все это весьма нестрого, но позволяет качественно понять, почему в отраженной волне будет сдвиг фаз, а приходящая вглубь металла волна будет постепенно исчезать: вторичные волны, испущенные свободными электронами в направле нии падающей волны, постепенно компенсируют ее.

Любые среды, содержащие свободные электроны, по-

глощают прошедшую волну. Ее энергия переходит в джоулево тепло. Поэтому металлические зеркала нельзя использовать для мощных световых пучков (лазерных лучей). Они нагревают и испаряют металл (пример - лазерная резка металлов).

При чистом отражении коэффициент преломления среды будет мнимым. Если есть и отражение, и поглощение света, то

90

коэффициент преломления становится комплексным, его записывают в виде: n nR inZ (в идеальном диэлектрике nZ 0 до предельного отражения и nR 0 после). Постоянные

nZ , nR и коэффициент отражения света от металла R

Eотр 2

Eпад

называются оптическими постоянными металлов. По отра-

жению света можно определить величины nZ , nR которые связаны со структурой, концентрацией свободных электронов и т.п.

Это можно сделать: из формул Френеля

В отраженном свете Eпад и Eпад получают сдвиг по фа-

зе. Отраженный свет остается линейно поляризованным только в том случае, когда в падающем свете Eпад Eпад или Eпад Eпад . В остальных случаях .и r Eпад r Eпад

т.е. отраженный свет приобретает эллиптическую поляри-

зацию.

Построив эллипс можно по его полуосям и по эксцен-

лить nR и nZ . Это - метод Фурье.

Дополнительную информацию можно получить из коэффициента отраже ния света от металла. Рассмотрим случай нормального отражения. Тогда для обеих поляризаций и

91

получаем одинаковые формулы, и поляризацию можно не учитывать:

R - коэффициент отра жения для чистой поверхности. Приведем величины оптических постоянных некоторых

металлов:

Металлы с большим nZ можно использовать как зеркала (но не для очень большого светового потока). Заметьте, как блестят никелированные поверхности. Для разных длин волн λ коэффициент отражения металлов разный. При приближении к некоторой резонансной частоте 0 колебаний свободных элек-

тронов, падающая волна начинает очень сильно поглощаться. Выясним структуру прошедшей в металл (преломлен-

ной) волны. Для простоты – в случае нормальной волны без учета поляризации.

гера. Амплитуда убывает в e раз, а интенсивность прошедшего света в e2 раз (практически до нуля) уже при проникновении на глубину. Для большинства металлов nZ 2 5, т.е. свет в видимой области спектра проникает вглубь металла только на глу-

бину z 500нм 40нм(для серебра эта толщина уменьшает-

2 2

ся еще в 10 раз). Здесь надо учесть два явления - поглощение и отражение света. При сильном поглощении nZ велико и свет не проходит вглубь металла, но одновременно очень велика доля отраженного света, так что реально доля поглощенного света мала. При слабом поглощении nZ мало и свет проникает далеко вглубь металла (прозрачность электролитов), но отражение мало и практически весь свет поглощается средой.

93

Вопросы

1. Сформулируйте граничные условия для векторов поля волны, которые полностью определяют законы отражения и преломления света.

2.Можно ли определить длину световой волны, исследуя отражение или преломление света?

3.Известно, что частота света не меняется при переходе из одной среды в другую. Что можно сказать в этом случае о длине световой волны?

4.Почему экспериментальная проверка формул Френеля может быть выполнена наиболее эффективно при углах Брюстера?

5.Почему металлы хорошо отражают видимый свет?

6.Чем определяется коэффициент отражения

94

4 Основы кристаллооптики

Лекция 10

Двойное лучепреломление Дихроизм

Степень поляризации Поляризаторы

Поляризацией называется наличие у электромагнитной волны определенного закона, по которому в пространстве изменяются вектора электрического и магнитного поля.

Так плоско поляризованной волной называется такая волна, в которой вектора Е и Н колеблются в одной плоскости.

Круговая поляризация, когда вектора Е и Н вращаются в процессе распространения волны и т.д.

Для понимания данного явления необходимо знать:

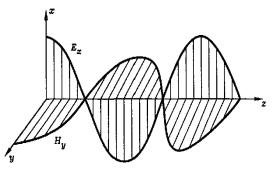
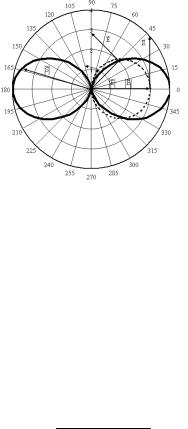
Рис.10.1. Структура бегущей электромагнитной волны. 1. Электромагнитная волна – поперечная волна, в кото-

рой вектора Е и Н колеблются в направлениях перпендикулярных к направлению распространения волны. Этот факт выража-

ется вектором Умова – Пойнтинга S= E H . Плоскость в ко-

торой колеблется вектор Е называется плоскостью колебаний, плоскость в которой колеблется вектор Н называется плоскостью поляризации. На рис. изображена структура бегущей электромагнитной волны.

95

2.Вектор E t iEx t jEy t kEz t (10.1).

3. При падении электромагнитной волны на вещество в нем возникают вторичные электромагнитные волны, вызванные вынужденными колебаниями зарядов в веществе под действием электрической составляющей падающей волны.

Результирующая напряженность поля в любой точке пространства складывается из первичной (падающей) волны и вторичных волн вызванных ускоренным вынужденным движением зарядов вещества под действием напряженности поля падающей волны.

E E0 Eiвв , (10.2)

i

Вторичное излучение может быть вызвано квазисвободным движением электронов и ионов в ионосфере и металлах, связанным движением электронов в молекулах (дипольное излучение) и т.д.

4. Колеблющийся диполь излучает электромагнитные волны по закону:

где: P- дипольный момент. Интенсивность излучения т.е. среднее значение потока энергии за период колебаний:

96

Рис. 10.2. Пространственная направленность излучения диполя.

Таким образом, практически все излучение зарядом происходит в направлении перпендикулярном к направлению колебания заряда.

5. Показатель преломления электромагнитной волны зависит от частоты падающей на вещество волны и собственной частоты колебаний диполей в веществе 0 и при нормаль-

ной дисперсии:

Перечисленных выше фактов достаточно для объяснения большинства поляризационных эффектов.

Получение плоской, круговой и эллиптической поляризации

Рассмотрим плоскую гармоническую волну распространяющуюся в направлении Z. Согласно выражения (10.1) представим:

97

Ex Ex0 cos t kz x

Ey Ey0 cos t kz y

t kz

Ex Ex0 cos cos x sin sin x Ey Ey0 cos cos y sin sin y

Отсюда

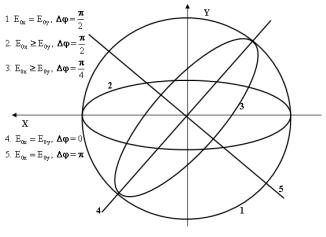
Рис. 10.3. Возможные результаты сложения взаимно перпендикулярных колебаний.

Возводя в квадрат, правые и левые части этих уравнений и складывая,получаем

sin2 , = y x

При распространении плоской гармонической волны конец вектора Е в плоскости Z=const описывает фигуры представленные на рис.

98

Двойное лучепреломление

В оптически анизотропных веществах наблюдается явление двойного лучепреломления.

Двойное лучепреломление это явление разделения луча на две составляющие при прохождении анизотропного вещества.

Оптически анизотропное вещество это вещество, в котором показатель преломления разный в разных направлениях. Ярким примером оптически анизотропного вещества являются кристаллы (за исключением кубических кристаллов).

Ионы или молекулы находящиеся в узлах кристаллической решетки кристаллов с точки зрения электрических свойств представляют собой электрические диполи образованные положительно заряженными ядрами атомов и электронным облаком вокруг. Произвольные колебания объемного электрического диполя могут быть представлены независимыми колебаниями вдоль осей кристалла с некоторыми собственными частотами.

Согласно выражений (10.4) и (10.5) показатель преломления в определенном направлении определяется соотношением частот падающей волны и собственной частоты диполей в

направлении перпендикулярном к рассматриваемому. На рис. 10.4 изображен анизотропный кристалл, в котором в двух направлениях Y и Z собственные частоты равны, в направлении же X собственная частота другая. Пусть плоская волна падает на кристалл в направлении X. Составляющие вектора напряженности электрического поля Ey и Ez вызовут колебания дипольных моментов кристалла в направлениях соответственно Y и Z и соответственно вторичное излучение в плоскостях перпендикулярных к этим направлениям. Поскольку собственные частоты дипольных моментов в направлениях Y и Z равны, то и показатели преломления в направлениях X,Y,Z будут равны для составляющих вторичной волны. Поэтому разделения волны на составляющие в кристалле для волны, падающей в направлении

X не происходит. Направление в котором не происходит

двойного лучепреломления называется оптической осью кристалла. По количеству оптических осей кристаллы разде-

ляют на одно, двух осевые. Плоскость образованная падаю-

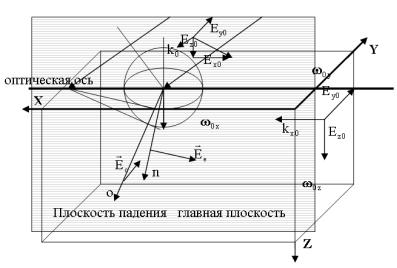
99

щим лучом и оптической осью называется главной плоскостью или главным сечением.

Рассмотрим случай падающего луча в плоскости Z0X, т.е. главная плоскость совпадает с плоскостью падения (в случае, когда плоскость падения не совпадает с главной плоскостью, необыкновенный луч преломляется в главной плоскости, а не в плоскости падения). В этом случае вторичное излучение диполей колеблющихся в направлении X с частотой ω0x будет иметь фазовую скорость в направлениях Y и Z меньше, чем фазовая скорость в направлении X, поскольку

Рис. 10.4. Прохождение лучом анизотропного кристалла.

0y 0z 0x , = const,

nox noz noy no

ney nez ne nex nox no Vox Voy Voz Vex Voy Voz

Таким образом, падающий луч раздваивается в кристалле на обыкновенный и необыкновенный лучи. Вектор E в обыкновенном луче перпендикулярен главной плоскости. Показатель преломления обыкновенного луча не зависит от направления в кристалле. Вектор E в необыкновенном луче лежит в главной плос-

100

кости. Показатель преломления необыкновенного луча зависит от направления в кристалле.

осью и направлением в кристалле.

Одноосные кристаллы разделяют на положительные и отрицательные кристаллы. Положительные, если ne no , отри-

цательные если ne no .

Для построения обыкновенного и необыкновенного лучей используются лучевые поверхности и принцип Гюйгенса. Лучевая поверхность (волновая поверхность), это поверхность

которую достигает луч за некоторое время r V t (см. рис. 10.4). В случае если падающий луч перпендикулярен оптической оси и поверхности кристалла, то обыкновенный и необыкновенный лучи двигаются в одном направлении, но с разными скоростями.

Дихроизм

Существуют кристаллы, в которых один из лучей (o или e) поглощается сильнее другого. Это явление и называют дихроизмом. Очень сильный дихроизм присущ кристаллу турмалина (минералу сложного состава). В нем обыкновенный луч практически полностью поглощается на длине около 1 мм.

Явление дихроизма используют для изготовления поляризаторов в виде светофильтров, их называют поляроидами (герапатитовые и др.). Они представляют собой тонкую (~0,1 мм) пленку, линейно поляризующую проходящий через нее свет.

Степень поляризации

Помимо плоскополяризованного и естественного света существует еще «промежуточный» случай — частичнополяризованный свет. Частично-поляризованный свет, как и естественный, можно представить в виде наложения двух некогерентных плоскополяризованных волн с взаимно перпендикулярными плоскостями поляризации, но разными по интенсивности. Его также можно рассматривать как смесь (сумму) естественного (ест) и плоско поляризованной (пол) составляющих.