
Курс лекций Оптическая физика
.pdf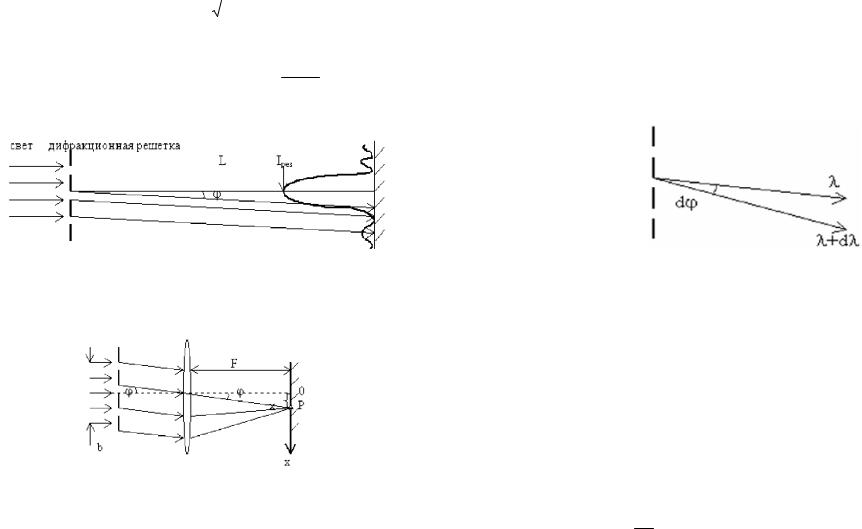
261
Так как угол <<1 но N может быть не мало, то имеем трансцендентное уравнение
|
|
|
2 |
Nd |
|
|
|
|
|
||||
N2 |
|
sin |
|
|
|
|
|
|
x |
|
|||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
или |
sinx. |
|||||
|
|
|
|
|
|
|
|||||||
2 |
|
|
d |
|
|
|
|
|
|||||
|
|
|
|
2 |
2 |
|
|||||||
( |
) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||
Корень этого уравнения х = 1,39, откуда получаем ши-
рину интерференционного максимума 2 2,78 .
Nd
Если экран, на котором наблюдают, спектры очень удален, то можно не использовать собирающую линзу.
Рис. 22.11. Дифракция от удаленного экрана.
Лучи, вышедшие под одним углом , соберутся практически в одну точку экрана. Но не совсем в одну. Поэтому такая схема не может использоваться для точного определения λ или разделения λ и λ+δλ.
Рис. 22.12. В спектрометрах экран находится
вфокальной плоскости собирающей линзы-объектива.
Вспектрометрах экран находится в фокальной плоскости собирающей линзы-объектива.
262
Если b - ширина падающего светового пучка, то N - чис-
ло освещенных щелей, и N=b/d.
Координаты максимумов (светлых полос) на экране xmax Ftg max ,гдеsin max m /d
Лучи света попадают в одну точку, и такой спектрометр используется для точного определения λ.
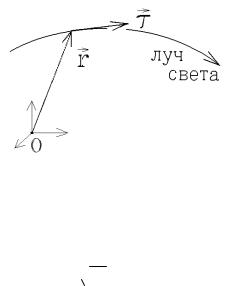
Кроме того, дифракционная решетка характеризуется
угловой дисперсией
D |
d |
|
m |
(22.10) |
|
dcos |
|||
|
d |
|
||
Рис. 22.13. Угловая дисперсия.
Чем больше угловая дисперсия, тем сильнее расходятся лучи в области интерференционного максимума (тем шире полоса спектра).
Свободной областью дисперсии решетки λ- это ми-
нимальная ширина спектрального интервала, при котором спектры соседних порядков еще не перекрываются:
(m+1) λ =m(λ + λ ), λ = λ /m
Спектры m= 0, 1 вообще не перекрываются.
Так для типичной решетки для исследования оптического диапазона (N=2400) видимый спектр начнет перекрываться при m = 2.
Линейная дисперсия Dl определяет линейное расстояние dl в фокальной плоскости линзы между линиями спектра и + d , т.е.
dl Dl d .
263
Для малых углов d можно dl определить как dl = F d , где F – фокусное расстояние линзы. Тогда
Dl = F D . |
(22.11) |
Вопросы:
1.В чем заключается физическое содержание принципа Гюйгенса?
2.Перечислите основные трудности метода зон
Френеля.
3.Как качественно зависит интенсивность пятна Пуассона от расстояния до непрозрачного экрана?
4.Каковы условия применимости приближения Френеля и приближения Фраунгофера?
5.Можно ли наблюдать дифракцию Фраунгофера на малых расстояниях?
6.Чем объясняется большая дисперсионная область дифракционной решетки?
7. При каком условии m-й главный |
максимум |
для дифракционной решетки с периодом d |
и шириной |
щели b обращается в нуль?
8. Для чего нужны большие фокусные расстояния в современных монохроматорах ?
264
10. Геометрическая оптика
Лекция 23
Геометрическая оптика Основные положения геометрической оптики
Уравнение эйконала и принцип Ферма
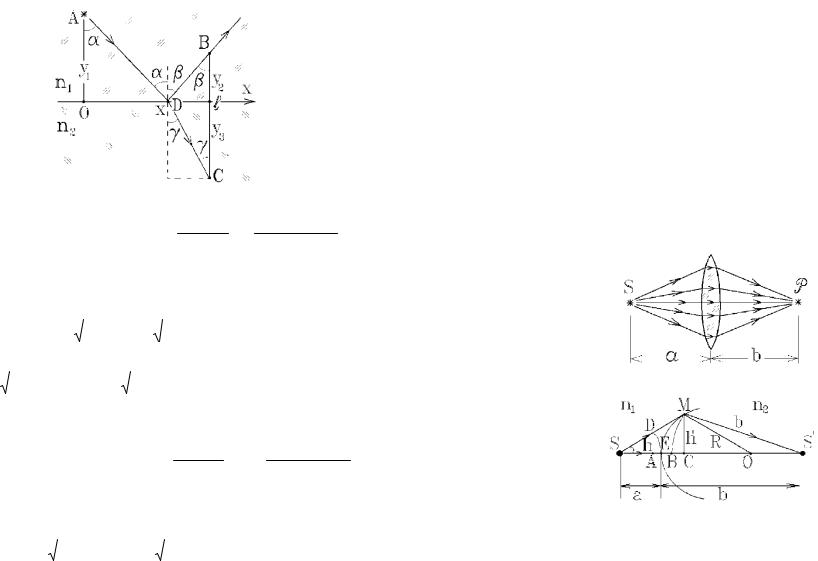
Если амплитуда светового вектора и направление его колебаний практически не изменяются на расстоянии ~λ и волновые поверхности имеют небольшую кривизну, то свет распространяется вдоль линий - лучей. Касательная к лучу перпендикулярна волновой поверхности и направлена вдоль скорости (вектора Пойнтинга света).
Это приближение λ 0 или геометрическая оптика.
Рис. 23.1. Геометрия светового луча.
Рассмотрим геометрию такого луча света с волновой функцией E E0 exp(i( t kr) соответствующей плоской
волне. Вводим единичный вектор k / k, направленный вдоль скорости волны, т.е. вдоль светового луча. В среде с пока-
зателем преломления n 
 скорость электромагнитной вол-
скорость электромагнитной вол-
ны V c/n и |
ее длина волны VT cT/n 0 /n в n раз |
|||
меньше, чем |
в |
вакууме. Тогда |
волновое |
число |
k 2 / 2 n/ 0 |
k0n будет в n раз больше, чем в вакуу- |
|||
ме. Подставляя |
|
|
exp(i( t k |
|
k k0n , находим E E0 |
0n r) |
|||

265
Рис. 23.2. К выводу эйконала.
В среде с n=const такая плоская волна (луч) будет распространяться по прямой линии. Но в среде с непостоянным показателем преломления n n(r)луч искривлен.
Решение для волновой функции в такой среде ищут в
виде где скалярную функцию
S S(r) называют эйконалом.
Если показатель преломления среды изменяется не очень быстро, то эйконал можно разложить в ряд вблизи некоторой точки с радиус-вектором r0 и ограничиться первыми двумя членами ряда (эйкональное приближение)
|
|
|
dS |
|
|
|
|
|
|
|
S(r) S(r0 ) |
dr |
r |
r |
(r r0 ) ... |
|
|
||||
|
|
|
|
|
0 |
|
|
|
|
|
Подставляя это разложение в искомое решение, получа- |
||||||||||
ем уравнение плоской волны |
|
|
|
|
||||||
|
E E0 exp(i( t k0n r). От- |
|||||||||
|
|
|
dS |
|
|
dS |
|
|||
сюда находим |
k0n r k0 |
dr |
r |
или n |
dr |
S (23.1) |
||||
Это основное уравнение геометрической оптики или уравнение эйконала. Проинтегрируем уравнение эйконала вдоль траектории луча, распространяющегося из точки 1 точку 2 (рис. 23.2):
2 |
|
2 |
dS |
|
2 |
n dr |
|
dr dS S2 S1 |
|||
1 |
|
1 |
dr |
|
1 |
266
Результат интегрирования не зависит от траектории. Но если двигаться вдоль истинной траектории луча, то лишь для этой траектории угол между векторами dr и равен 0° и с уче-
том |
|
dr |
|
d получаем |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
n dr n |
|
|
|
|
|
dr |
|
cos00 |
nd S2 |
S1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина nd называется оптической длиной пути лу- |
||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ча. |
|
|
Для |
|
любой |
|
|
другой |
произвольной |
траектории |
||||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
n dr |
/ |
|
nd / cos (S2 S1) nd / . |
Получили общий |
||||||||||||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
принцип, позволяющий определить истинное направление движения (светового) луча:
В любой среде луч движется по пути с наименьшей оптической длиной:
2
(S2 S1 ) nd min (23.2) {при этом оптическая
1
длина пути равна изменению эйконала).
Это принцип Ферма, определяющий ход лучей в оп-
тике. Подставляя сюда n=c/V, находим
2 |
2 |
d |
2 |
|
nd с |
c dt c t min (23.3). Отсюда вторая форму- |
|||
V |
||||
1 |
1 |
1 |
||
лировка принципа Ферма:
Луч (света) распространяется по такому пути, который преодолевается им за наименьшее возможное время.
Уравнение эйконала дает приближенное решение уравнений Максвелла в случае λ 0 или k . Поэтому из этого уравнения или из принципа Ферма можно получить некоторые законы, полученные в волновой оптике.
Закон преломления света. Пусть луч света из точки А с координатой х=0 падает на плоскую границу двух сред с показателями преломления n1 и n2 в точке Д с координатой х и отра-
267
жаясь или преломляясь, проходит через точки В или С с координатой x . По принципу
Рис. 23.3. К выводу закона Снеллиуса-Декарта. Ферма оптическая длина пути
B
Lотр nd n1(AD DB) n1 (
 y12 x2
y12 x2 
 y22 ( x)2 )
y22 ( x)2 )
A
должна быть минимальной на пути реального отраженного луча,
|
dLотр |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
( x) |
|
|
|
|
|||
т.е. |
|
0 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Отсюда |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
dx |
|
|
|
1 |
|
2 |
x |
2 |
2 |
( x) |
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
y1 |
|
|
|
|
|
|
|
y2 |
|
|
|
|
||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
( x) |
|
|
|
|
||||||
sin |
|
|
|
|
|
|
, |
sin |
|
|
|
|
|
|
|
|
|
|
,sin sin , |
(23.4) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
y12 x2 |
|
|
|
|
|
|
|
y22 ( x)2 |
|
|
|
|
||||||||||
т.е. угол падения равен углу отражения.
Аналогично, для преломленного луча должна быть минимальна величина
B
Lпр nd n1AD n2DC n1 
 y12 x2 n2
y12 x2 n2 
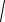 y32 ( x)2 )
y32 ( x)2 )
A
, т.е.
dLпр |
|
|
|
|
x |
|
|
|
( x) |
|
|
|
||||
|
0 n |
1 |
( |
|
|
|
) n |
2 |
( |
|
|
|
) n |
1 sin n |
2 |
sin |
dx |
|
|
|
|
|
|
||||||||||
|
|
|||||||||||||||
|
|
|
|
y12 x2 |
|
|
|
y32 ( x)2 |
|
|
|
|||||
, т.е.
n1 sin =n2 sinγ (23.5).
268
Получили закон преломления (закон СнеллиусаДекарта).
Подобным же образом из принципа Ферма можно вывести формулу линзы.
Формула линзы.
Испущенные из точки S лучи одновременно (согласно принципу Ферма через наименьшее возможное время) соберутся в точке Р, давая изображение источника S.
Действительно, источник света S находится в среде с показателем преломления n1 на расстоянии а от сферической поверхности радиуса R , отделяющей среду с показателем преломления n2.
Лучи света соберутся в точке S', давая изображение источника (на расстоянии b от поверхности раздела сред).
Cоберутся только те лучи, для которых выполняется
условие параксиальности, т.е. которые расходятся под очень малыми углами а к оптической оси.
Рис. 23.4. Ход лучей в тонкой линзе.
Т.е. все формулы линз, используемые в геометрической оптике, справедливы только для параксиальных лучей и с помощью фотоаппарата из таких линз нельзя снимать предметы вблизи (а вдали - теряются детали предмета).
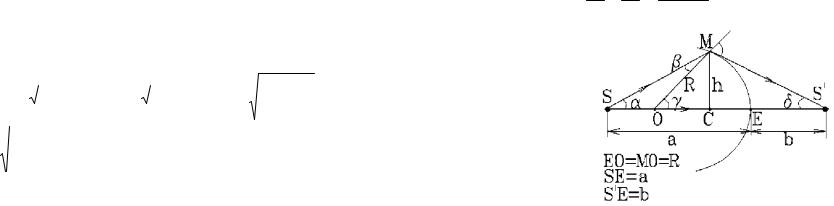
269
По принципу Ферма оптические длины всех лучей, собирающихся в точке S', одинаковы, т.е.
n1 SM n2 S/ M n1a n2bили, если провести окружность радиусом SD=SE=a и S/M=S/B=b, то DMn1=BEn2. Для параксиальных лучей 0 и h h/; DM AC=AE+EC
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Но |
|
|
|
SD |
|
|
h |
|
|
a |
|
|
|
a |
|
|
h |
|
|
a a 1 |
|
|
|
|
. Т.к. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|||
h |
|
|
|
h |
2 |
|
|
|
|
|
1 h |
|
2 |
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
1, 1- |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
, AE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Аналогично находим ВС и ЕС. Тогда |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
BE EC BC |
h2 |
|
|
h |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому |
||||||||||||||||||||||
|
|
|
|
|
2R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2b |
|
n1 |
|
|
|
n |
|
|
n2 |
n1 |
|
|
|
|
|||||||||
h2 |
|
h2 |
|
|
|
|
|
|
|
|
h2 |
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
n |
2 |
или |
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
2a |
|
2R |
|
|
|
|
|
2R |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
|
|
R |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Получили формулу сферической поверхности (аналогична формуле линзы).
Если источник S находится на бесконечном удалении: a= , то он создает пучок параллельных лучей, которые должны сойтись в фокусе: b=F т.е.
n1 |
|
n2 |
|
n2 n1 |
|
n2 |
D (23.6) |
|
|
R |
F |
||||
a b |
|
|
|
||||
Величина D называется оптической силой сферической поверхности.
Пусть теперь лучи от источника S падают на вогнутую поверхность раздела двух сред (см.рисунок).Тогда = - ; = -; γ= +δ и для параксиальных лучей (малые углы)
sin h/R; tg h/a; tg h/b, а из закона пре-
ломления. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n |
3 |
|
sin |
|
|
|
|
, n |
|
h |
|
h |
n |
|
h |
|
h |
||||
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
т.е. |
||||||||
|
n2 |
sin |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
R |
|
b |
|
R |
|
a |
|||||||||||
270
или n3 n2 n2 n3 b a R
Рис. 23.5. Вогнутая линза.
Оптическая сила вогнутой поверхности
D |
n3 |
|
n2 n3 |
, |
(b = F при a = ). |
|
|
F R
Отсюда следует, что лучи могут собраться в одной точке S/ только при n3<n2, фокусные расстояния для сферической поверхности одинаковы Fслева=Fсправа при n3=n2.
Как видим, сферическая граница раздела двух сред сама обладает свойствами тонкой линзы.
Оптические силы двух близко расположенных преломляющих поверхностей складываются, и мы получаем формулу для определения оптической силы тонкой линзы:
|
|
n |
л |
n |
с |
|
n |
л |
n |
с |
|
n |
с |
|
|
|
1 |
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
D |
линзы |
|
|
R |
|
|
|
R |
|
|
|
F |
|
(nл |
n |
|
|
|
R |
|
||||
|
|
|
|
|
|
|
с ) R |
|
|
|
||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
линзы |
|
|
|
|
1 |
|
|
2 |
|
|
Эти законы годятся не только для света, но и для любой другой электромагнитной волны. Чем меньше ее λ, тем заметнее лучевые свойства.
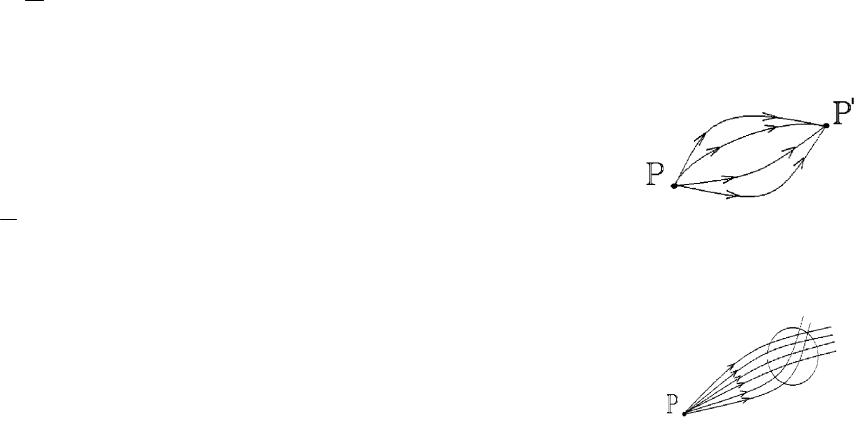
271
Распространение света в неоднородной среде
Снова рассмотрим истинную траекторию луча. Продифференцируем уравнение эйконала по в d , т.е. по длине, от-
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
dn |
|
d |
dS |
||||
считанной вдоль траектории луча. |
|
|
(n ) |
|
n |
|
|
|
|
||||||||||||
d |
d |
d |
d |
||||||||||||||||||
Подставляя |
|
в |
это |
|
|
|
|
|
|
|
уравнение |
||||||||||
|
dS |
dS dr |
|
|
|
|
dn |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
dr |
|
|
S n n, |
|
|
n |
|
находим |
|||||||||
|
d |
|
d |
|
d |
|
|||||||||||||||
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
|
|
( n) n |
(23.7). |
|
|
|
|
|
|
|
|
|
||||||||
d |
|
|
|
|
|
|
|
|
|
||||||||||||
Это уравнение описывает движение луча в среде с неоднородным показателем преломления n(r).
Введем теперь радиус кривизны траектории луча R. Здесь en - единичный вектор, задающий направление
нормали к траектории. Т.к.d Rd ,d |
|
|
|
d en , то |
d |
|
en |
|
|
|
|||||||
|
|
d |
R |
|||||
|
|
|
|
|
|
|||
, и уравнение траектории луча принимает |
вид |
|||||||
nen ( n) n. Умножая обе части этого уравнения ска-
R
2 |
|
|
n |
|
|
лярно на en , получаем, с учетом en |
1,en |
0 |
|
en |
n |
R |
Отсюда следует, что луч отклоняется в область с большим пока-
зателем преломления: R > О при n 0.
Это объясняет возникновение миражей, иллюзии водной глади над нагретым асфальтом, астрономической рефракции.
272
Лекция 24
Центрированные оптические системы и ход лучей в них
Условие синусов Аббе или теорема Лагранжа-Гельмгольца
Три основные матрицы преобразования луча Аберрации оптических систем
Гауссов пучок
Если пучок лучей, вышедших из точки Р после всех преломлений, отражений и искривлений сходится в одной точке P/,
то такой пучок называется гомоцентрическим. Точка P/
называется стигматическим (точечным) изображением точки Р.
Рис. 24.1. Гомоцентрический пучек.
Если поменять местами точки P и P/, то лучи, вышедшие из точки P/ сойдутся в точку Р. Это принцип обратимости, следующий из принципа Ферма: оптические пути всех лучей между точками Pи P/ (которые называются сопряженными) - одинаковы.
Рис. 24.2. Не стигматическое изображение.
К сожалению, стигматическое изображение получить трудно. Обычно лучи от точки Р пересекаются в некоторой области. Так в параболическом зеркале лучи пересекутся не в од-
273
ной точке, если источник расположен не на оси параболы. К тому же в одной точке будет наблюдаться дифракционное уширение (диск Эйри).
Стигматическое схождение гомоцентрического пучка удается получить в центрированных оптических системах, когда центры кривизны всех сферических отражающих и преломляющих плоскостей лежат на одной прямой, называемой главной оптической осью, а пучки лучей параксиальные, т.е. образуют малые углы с оптической осью.
Рис. 24.3. Центрированная оптическая система.
Это - Гауссова оптика ( теорию таких оптических систем разработал Гаусс в 1841 г.)
Изображение протяженного предмета будет резким (контрастным), если оптическая длина лучей между всеми сопряженными точками предмета и изображения одинакова.
Тогда, если лучи BB/ и AA/ выходят из противоположных точек А и В предмета параллельно под углом к оптической оси, то они пересекутся в точке D на фокальной плоскости, а затем дадут изображение A/B/. Их наклон к оптической оси будет практически одинаковым и равным /, если предмет мал.
Условие равенства оптических путей, пройденных этими
лучами: BC n=A/C/ n/ или
AB n sin =A/B/ n/ sin /
Последнее уравнение - это условие синусов Аббе или теорема Лагранжа-Гельмгольца.
Если гомоцентрический пучок выходит из точки предмета АВ, находящегося в среде с показателем преломления n рас-
274
ходясь под углом , а сходится в сопряженную точку изображения А'В' в среде с показателем преломления n/ под углом /, удовлетворяющим условию Аббе, то изображение будет резким и апланатическим.
Вместо того чтобы определять путь луча с помощью законов преломления и т.п. используют метод матриц.
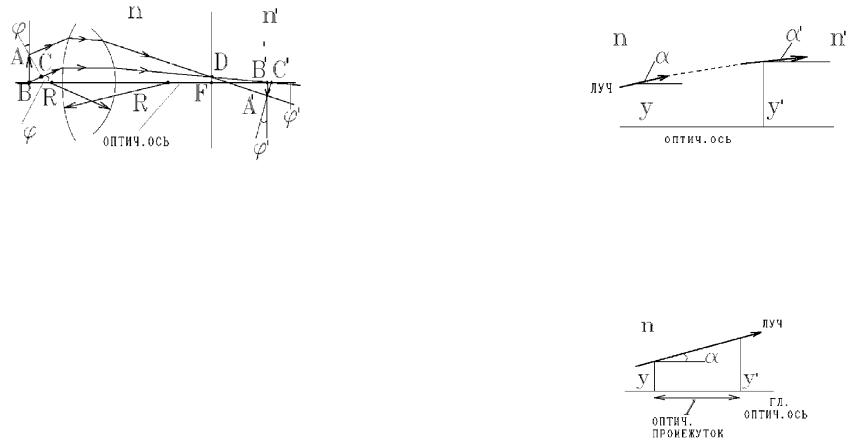
Положение и направление геометрического луча в каждой точке оптической системы задают отклонением у от главной оптической оси и малым углом наклона к этой оси, умноженным на показатель преломления среды данной точке n .
Рис. 24.4. Ход луча в неоднородной среде.
В другой точке этот луч имеет другие величины y/ и n/ /, которые связаны с исходными матрицей:
y/ |
|
A B y |
|
|
/ |
/ |
|
|
. |
n |
|
C D n |
||
Достаточно знать три основные матрицы преобразования луча:
1). В однородной среде с одинаковым nср луч идет по прямой
Рис. 24.5. Ход луча в однородной среде.
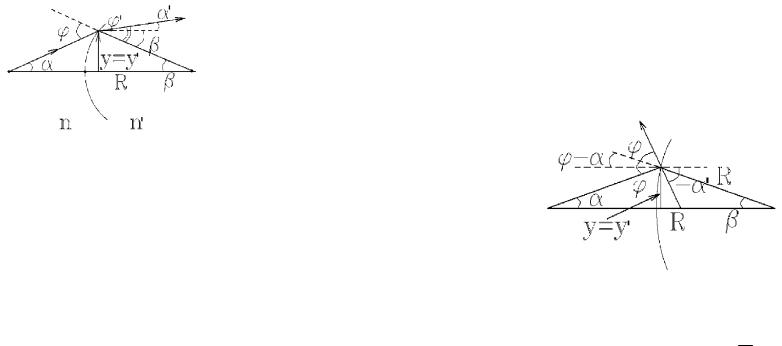
275
и, проходя расстояние вдоль оптической оси {оптический
промежуток), приобретает параметры
|
/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
y tg y . |
|
|
|
||||||||||
|
|
|
|
|
|
nСР |
|
|
|
|
|
|
|||
Очевидно |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
y/ |
|
|
|
|
y |
|
|
|
y |
|
, |
||||
|
|
|
|||||||||||||
|
|
|
|
|
|
n |
|
|
|
nСР |
|
||||
nСР |
|
|
|
СР |
|
|
0 1 |
nСР |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
где MОП |
|
|
|
|
|
- матрица оптического промежутка. |
|||||||||
|
|
|
|||||||||||||
|
|
|
|
nСР |
|||||||||||
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2). Луч идет, преломляясь на сферической поверхности радиуса R>0,
Рис. 24.6. Преломление луча на сферической поверхности.
если центр сферы справа от поверхности и R<0 если центр сферы слева от поверхности).
Слева и справа от поверхности y=y/ (см. рис. 24.6). Очевидно, что = + , /= /+ . По закону преломления,
на поверхности,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
276 |
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
nЛ |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
nЛ |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
тогда |
|
|
R |
|
|
и |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
sin / |
|
/ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
СР |
|
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
y |
|
|
n |
СР |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
/n |
|
n |
|
|
|
|
(n |
|
|
|
n |
|
), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Л |
СР |
|
|
СР |
Л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
y |
/ |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
y |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
СР |
Л |
|
|
|
|
|
|
|
|
|||||||||||
|
/ |
|
|
|
nСР |
|
|
|
|
|
nСР ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
n |
Л |
|
|
R |
(nЛ |
|
|
|
|
|
R |
|
|
|
|
|
|
1 |
nСР |
||||||||||||||||||||||||
|
|
|
|
т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
0 |
|
матрица |
|
преломляющей |
|||||||||||||||||||
|
|
|
|
MПРЕЛ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
DПРЕЛ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
сферической поверхности, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
DПРЕЛ |
|
nЛ nСР |
|
|
- |
оптическая |
|
сила |
|
|
сферической |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
поверхности. Плоская поверхность -частный случай сферической поверхности при R= .
3) Сферическая отражающая поверхность радиуса
R>0
Рис. 24.7. Сферическая отражающая поверхность.
если центр справа, R<0 если центр слева).
Легко видеть (рис. 24.7):
/ ( ), y ,
R

277
|
|
/ |
2 |
2y |
откуда |
|||||||||
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
0 |
|
R |
|
|
||
|
y/ |
|
|
|
|
|
y |
|||||||
|
|
|
|
|
2n |
СР |
|
|
|
|
и |
|||
|
|
/ |
|
|
|
|
|
1 |
|
|
|
|
||
|
|
R |
|
|
|
|||||||||
nСР |
|
|
|
|
nСР |
|||||||||
|
|
M |
|
|
|
|
|
1 |
|
0 |
- матрица отражающей сфери- |
|||
|
|
|
|
|
2nСР |
|
|
|||||||
|
|
|
|
ОТР |
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
R |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ческой поверхности.
Легко видеть, что эта матрица получается из матрицы преломляющей поверхности заменой nл = -nср.
Зная эти три матрицы MОП, Мотр и Мпрел легко рассчитать ход лучей в любой центрированной оптической системе:
|
y/ |
|
M |
|
M |
|
M |
|
M |
|
|
y |
|
|
/ |
|
|
ОП1 |
ПР1 |
ПР2 |
ОП2 |
|
|
||||
|
|
/ |
|
|
|
|
|
|
|||||
n |
|
|
|
|
|
|
|
|
|
n |
|||
Например, для тонкой линзы с радиусами R1 и R2, изображенной на рис. 24.8,
Рис. 24.8. Тонкая линза.
278
|
|
|
|
/ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
0 |
|
|
|
||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|||||
|
|
|
|
|
|
|
|
|
nЛ n |
СР |
|
|
|
|
|
nЛ |
nСР |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|||||||||||||||||||||||
|
|
/ |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
СР |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СР |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(n |
|
n |
|
|
|
)( |
|
|
|
|
|
|
) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Л |
СР |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
R1 |
|
|
|
|
|
n |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СР |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
MЛ |
|
|
|
|
|
|
|
|
- матрица тонкой линзы, |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
DЛ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
DЛ (nЛ n |
СР ) |
R1 |
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
оптическая сила тонкой линзы. Оптическая сила измеряется в диоптриях.
Параллельный пучок света, падающий на тонкую линзу слева, соберется в точке правого фокуса линзы:
y |
|
|
1 |
|
0 |
|
|
F |
|
|
0 |
|
|
|||
|
|
|
|
1 |
n |
|
|
|
|
|||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
DЛ |
1 |
|
|
nСР |
n |
СР |
/ |
|
|||||
0 |
|
|
0 |
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
/ |
|
|
|
|
|
|
|
|
|
|
|
|
nСР |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Fn |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
nСР |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Fn |
|
|
|
|
|
|
|
|
|
|
|
|
|
( DЛ |
|
1)( nСР / ) |
|
|
|
|
|||||||||
|
nСР |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 24.9. Фокус линзы.
279
Откуда nСР DЛ .
Fn
Определение правого фокусного расстояния тонкой линзы (оно равно левому фокусному расстоянию)
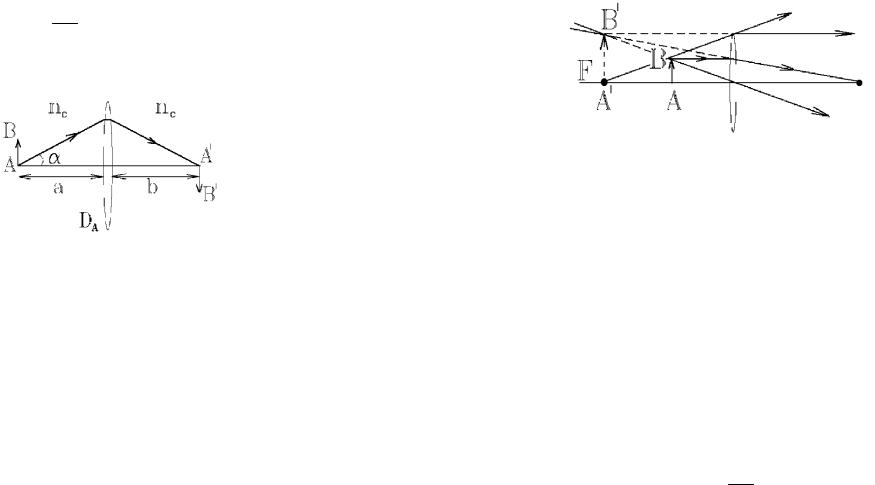
При построении апланатического изображения
Рис. 24.10. Построение апланатического изображения. луч, вышедший из точки предмета А на оптической оси, вернется на оптическую ось в точке A/ изображения, как изображено
|
|
|
|
|
|
|
|
|
n |
СР |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
на рис. 24.10: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
F |
|
DЛ |
|
(nЛ n |
СР ) |
R |
|
|
|
R |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
b |
|
|
0 |
|
||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nCP |
DЛ |
1 |
|
|
|
|
nCP |
|
/ |
|
|||||||||||||||||||||
|
|
nCP |
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
1 |
|
|
nCP |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
b |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
ab |
|
|
|
|
/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
Л |
|
|
|
|
|
|
n |
CP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
nCP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
nCP |
|
|
|
|
|
|
|
|
|
|
|
nCP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 DЛ |
|
|
|
|
|
|
|
nCP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nCP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
b |
|
|
|
|
a |
|
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
=0, т.е. получаем формулу тонкой |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Л |
|
|
|
2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
nCP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
nCP |
|
|
|
|
|
|
|
|
|
nCP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
линзы |
nСР |
|
nСР |
|
D |
Л |
|
|
nСР |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
280
Рис. 24.11. Изображение в тонкой линзе. Изображение в тонкой линзе образуется построением
трех лучей (рис. 24.11). При мнимом изображении точка лежит на продолжении лучей (расходящихся).
Параллельный пучок света пересекается в фокальной плоскости.
Коэффициент линейного увеличения: y//y=b/a.
Для системы двух тонких линз с оптическими силами D1D2на расстоянии друг от друга получаем матрицу
1 |
0 |
|
|
|
|
1 |
0 |
|
||
|
1 |
|
|
|
||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
1 |
|
|
nCP |
D2 |
1 |
|
|
|
|
|
0 |
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
1 D |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
nCP |
|
|
nCP |
|||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
D1 |
D2 D2D1 |
|
1 D1 |
|
|
|
||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
nCP |
nCP |
||||
откуда оптическая сила такой системы
DСИСТ D1 D2 D2D1 nCP
В общем случае толстой линзы или системы линз кроме фокусов и фокальных плоскостей вводят главные плоскости оптической системы (точки пересечения этих плоскостей с главной оптической осью и точки фокусов называются кардинальными точками оптической системы).
