Курс лекций Оптическая физика

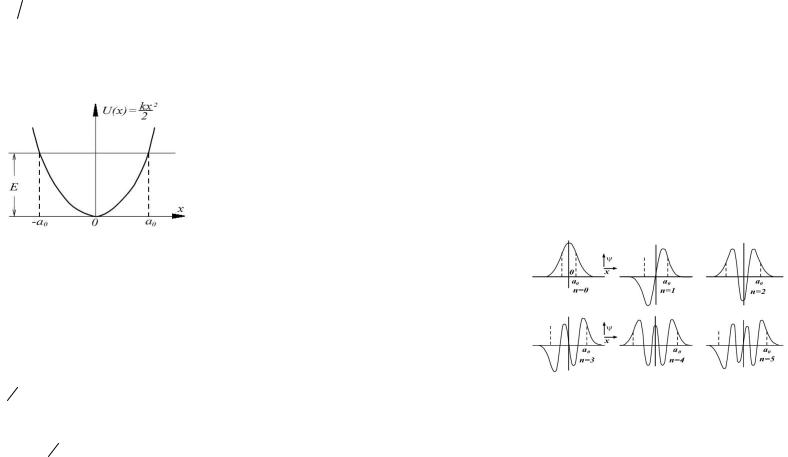
381

С классической точки зрения прохождение частицы сквозь потенциальный барьер при E U невозможно, так как, находясь в области барьера, она обладала бы отрицательной кинетической энергией. Т.е. туннельный эффект является специфическим квантовым эффектом, не имеющий аналога в классической механике.

Гармонический осциллятор. Пружинный, физический и математический маятники являются примерами классических осцилляторов. Потенциальная энергия гармонического осциллятора определяется выражением

где – собственная частота колебаний осциллятора, m – масса частицы. Амплитуда колебаний классического осциллятора xm определяется его полной энергией E. Классическая частица совершает движение в пределах ( xm , xm ).

Рис. 29.7. Параболическая потенциальная яма. Стационарные состояния квантового осциллятора опре-

деляются уравнением Шредингера

где E – полная энергия осциллятора. Уравнение (29.10) имеет конечные и непрерывные решения при собственных значениях энергии

En (n 12) (n 0,1,2,...) . (29.11)

Уровни энергии гармонического осциллятора являются равноотстоящими друг от друга. Наименьшее возможное значение энергии равно E0 12 . Это значение называется энерги-

382

ей нулевых колебаний. Существование минимальной энергии является типичной для квантовых систем и представляет прямое следствие соотношения неопределенностей.

Квантовая механика позволяет вычислить вероятности переходов из одного состояния в другое. Вычисления показывают, что для гармонического осциллятора возможны лишь переходы между соседними уровнями. При таких переходах квантовое число n изменяется на единицу

. (29.12)

Условие (29.12) на возможные переходы называется правилом отбора. Таким образом, энергия гармонического осциллятора может изменяться только порциями .

Графики волновых функций для значений квантового числа n от 0 до 5 представлены на рис. 29.8. Отрезок [-

a0,a0] определяет область, в которой совершал бы колебания классический осциллятор. Ширина этой области оказывается различной для разных значений квантового числа n, поскольку энергия осциллятора, а, следовательно, и амплитуда его колебаний также зависят от n .

Вне классической области [-a0,a0] волновые

ции Ψn отличны от нуля, что свидетельствует о том, что квантовый гармонический осциллятор с определенной вероятностью может находиться вне пределов параболической потенциальной ямы.

Рис. 29.8. Вид волновых функций при небольших значениях n.

При малых значениях квантового числа n плотность вероятности нахождения частицы, определяемая квадратом модуля волновой функции |Ψn(x)|2 , кардинальным образом отличает-

383

ся от плотности вероятности обнаружения классического осциллятора.

Рис. 29.9. При n=10 функция Ψn(x)|2 приближается к классической кривой распределения.

При значительной величине квантового числа n , например, при n=10 функция Ψn(x)|2 приближается к классической кривой распределения. Она достигает максимума вблизи точек поворота и резко спадает вне классической области движения (рис.). При n→∞ кривая вероятности Ψn(x)|2, как того и требует принцип соответствия, переходит в классическую функцию распределения плотности вероятности.

Отметим, что модель гармонического осциллятора и связанная с ним задача о движении частицы в параболической потенциальной яме является идеализацией, справедливой лишь при малых отклонениях колеблющейся частицы от положения равновесия. Во всех реальных ситуациях потенциальная энергия U(x) частицы, совершающей колебания около положения равновесия, имеет более сложный по сравнению вид. Поэтому при возрастании амплитуды колебаний, начиная с некоторых значений амплитуд, движение частицы будет все больше отличаться от гармонических колебаний. Такое движение называют ангармоническим движением, а соответствующий осциллятор - ангармоническим осциллятором. Однако в случае малых колебаний влияние энгармонизма ничтожно мало, что позволяет использовать модель гармонического осциллятора для описания колебательного движения квантово-механических систем.

Атом водорода. Рассмотрим систему, состоящую из неподвижного ядра с зарядом Ze и движущегося вокруг него электрона. При Z 1 система представляет собой атом водорода, при Z 1– водородоподобный ион.

384

Рис. 29.10. Потенциальная яма для водородоподобного атома.

Потенциальная энергия электрона равна

Следовательно, уравнение Шредингера имеет вид

Поле (29.13), в котором движется электрон, является центрально-симметричным, т. е. зависит только от r. Поэтому решение уравнения (29.14) наиболее целесообразно проводить в

сферической системе координат r,θ,φ, где оператор Лапласа 2 имеет следующий вид:

Не будем воспроизводить здесь этапы решения уравнения (29.14), поскольку оно слишком громоздко. Остановимся лишь на сути процесса решения и на анализе окончательных результатов. Решение уравнения (29.14) проводят методом разделения переменных с учетом естественных требований, налагаемых на ψ-функцию: она должна быть однозначной, конечной, непрерывной и гладкой. В теории дифференциальных уравнений доказывается, что решения уравнения (29.14) являются непрерывными, однозначными и конечными в следующих случаях:

385

-при любых положительных непрерывных значениях

энергии;

-при дискретных отрицательных значениях энергии. Первый случай соответствует свободному электрону

(заштрихованная область на рис. 29.10), второй — получаемым из уравнения Шредингера собственным значениям энергии.

Случай E 0 соответствует электрону, пролетающему вблизи ядра, т.е. свободному электрону. Случай E 0 соответствует электрону, движущемуся вблизи ядра, т.е. связанному электрону. Самый нижний уровень E1 , отвечающий минимально возможной энергии, называется основным, все остальные – возбужденными. Таким образом, квантование энергии атома является следствием теории, в отличие от теории Бора, в которой квантование вводилось как постулат.

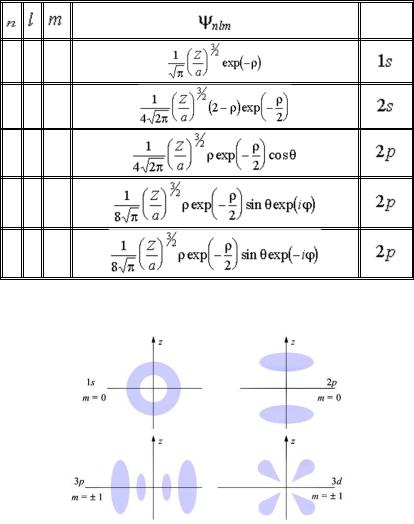
Собственные функции уравнения (29.14), представленные в сферической системе координат, содержат три целочисленных параметра: главное число n, орбитальное число l и магнитное число m

nlm (r, , ) .

Выпишем нормированные волновые функции

nlm (r, , ) для ряда квантовых состояний водородоподобных атомов (рис. 29.11).

На рис. 29.12. для некоторых квантовых состояний атома водорода, описываемых найденными волновыми функциями, показана радиальная электронная плотность вероятности в виде "облака", густота которого в разных точках пространства пропорциональна этой плотности вероятности. Именно так, в виде облака плотности вероятности может быть представлен образ атома в квантовой теории.

386

Состояние

1 0 0

2 0 0

2 1 0

2 1 + 1

2 1 - 1

Рис. 29.11. Нормированные волновые функции

nlm (r, , ) для ряда квантовых состояний водородоподобных атомов

Рис. 29.12. Радиальная электронная плотность вероятности в виде "облака", густота

которого в разных точках пространства пропорциональна этой плотности вероятности.

387

Квантовые числа и их физический смысл:

1.Главное квантовое число n определяет энергетиче-

ский уровень электрона в атоме в соответствии с формулой (29.19) и может принимать любые положительные целочисленные значения.

2.Орбитальное квантовое число l определяет орби-

тальный момент импульса электрона. Согласно законам квантовой механики момент импульса квантуется по правилу

При заданном n орбитальное число может принимать значения

Так как движущийся вокруг ядра электрон является заряженной частицей, то такое движение обуславливает протекание некоторого замкнутого тока в атоме, который можно оха-

рактеризовать орбитальным магнитным моментом pM .

В теории Бора, когда с позиции классической теории рассматривается круговое движение электрона по орбите радиуса r со скоростью v, величина орбитального механического момента равна L =m0vr . Если время полного оборота электрона T , то такому движению соответствует замкнутый ток

i e e T 2 r

где: e – заряд электрона, T – период обращения электрона, который можно охарактеризовать величиной магнитного момента

pM i r2 evr 2

Связь механического и магнитного моментов при этом определяется гиромагнитным отношением

Так как заряд электрона отрицателен, то для орбитального движения направление вектора магнитного момента

388

pM противоположно направлению вектора механического мо-

мента импульса L (рис. 29.13).

Точный квантовомеханический расчет гиромагнитного отношения также приводит к формуле (29.22).

служит единицей измерения магнитных моментов атомов и называется магнетоном Бора.

Правило отбора. Если атом переходит из одного квантового состояния в другое с испусканием (поглощением) фотона излучения, то возможны лишь такие переходы, для которых орбитальное квантовое число ℓ изменяется на единицу. Это правило, согласно которому для оптических переходов ∆ℓ = ±1 ,

называется правилом отбора. Наличие такого правила отбора

обусловлено тем, что электромагнитное излучение (фотон) уносит или вносит не только квант энергии, но и вполне определенный момент импульса, изменяющий орбитальное квантовое число для электрона всегда на единицу.

389

3. Магнитное квантовое число m определяет ориента-

цию орбитального момента в пространстве. Согласно законам квантовой механики величина проекции момента на некоторое направление z принимает дискретные значения

(29.25),

где m – магнитное квантовое число, которое при заданном l может принимать значения

m 0, 1, 2,..., l .

Таким образом, вектор момента импульса электрона в атоме может иметь в пространстве 2l 1 возможных ориентаций.

С точки зрения классического представления об элек-

тронной орбите, с учетом перпендикулярности вектора L к плоскости орбиты, соотношение (29.25) определяет возможные дискретные расположения электронных орбит в пространстве по отношению к направлению внешнего поля (рис. 29.14).

Рис. 29.14. Возможные дискретные расположения электронных орбит в пространстве по отношению к направлению внешнего поля.

Отмеченная выше связь механического и магнитного моментов атома позволяет с учетом (29.25)записать также возможные значения проекции магнитного момента атома на выделенное направление Z :

зависящие от значения магнитного квантового числа m.

Вырожденные состояния. Согласно (29.19) энергия электрона зависит только от главного квантового числа n. Каж-

390

дому собственному значению энергии En (кроме E1 ) соответ-

ствует несколько собственных функций nlm , отличающихся

значениями квантовых чисел l и m. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.

Состояния с одинаковой энергией называются вырожденными, а число различных состояний с каким-либо значением энергии называется кратностью вырождения соответствующего энергетического уровня.

Кратность вырождения энергетических уровней легко вычисляется путем подсчета возможных значений l и m. Каждому значению квантового числа l соответствует 2l 1 значений квантового числа m. Следовательно, число различных состояний, соответствующих данному n, равно

В атомной физике применяется условное обозначение состояний электрона с различными значениями момента импульса. Электрон, находящийся в состоянии с l 0 называется s-электроном (соответствующее состояние – s-состоянием), с l 1 – p-электроном, с l 2 – d-электроном, с l 3 – f- электроном и далее по алфавиту. Значение главного квантового числа указывается перед условным обозначением орбитального числа l. Поскольку l всегда меньше n, возможны следующие состояния электрона:

и т.д. Схему уровней энергии удобно изображать так, как показано на рис. 29.15.

Испускание и поглощение света происходит при переходах электрона с одного уровня на другой. В квантовой механике доказывается, что для орбитального квантового числа имеется правило отбора

Это означает, что возможны только такие переходы, при кото-

391

рых l меняется на единицу. Правило обусловлено тем, что фотон обладает собственным моментом импульса (спином s). Его величина вычисляется по общему правилу (29.20), где вместо l следует использовать s 1. Данное значение определяет максимальную величину проекции спина на избранное направление. Испускание или поглощение фотона, согласно закону сохранения момента импульса, приводит к изменению момента импульса атома, согласно с правилом (29.23).

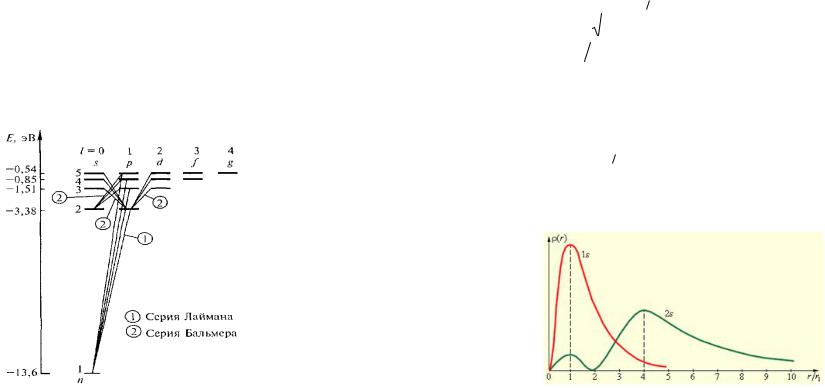
Рис. 29.15. Схема уровней энергии атома водорода. На рис. 29.15 показаны переходы, разрешенные прави-

лом (29.23). Серии Лаймана соответствует переходам np 1s (n 2,3,...);

серии Бальмера соответствуют переходы

и т.д.

Решение уравнения Шредингера для атома водорода дает, что волновая функция электрона в 1s состоянии является сферически-симметричной и имеет вид

нахождения электрона в шаровом слое радиуса r и толщиной dr равна

dP | |2 dV | |2 4 r2dr .

Подставив в формулу волновую функцию, получим

График радиальной плотности вероятности dP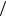dr для 1S и 2S состояний изображен на рис. 29.16.

Рис. 29.16. Радиальная плотность вероятности dPdr для 1S и 2S состояний

Ее максимум приходится на r rB . Таким образом, в основном состоянии атома водорода наиболее вероятное расстояние между ядром и электроном равно боровскому радиусу.

Спин электрона. Спиновое квантовое число. При классическом движении по орбите электрон обладает магнитным моментом. Причем классическое отношение магнитного момента к механическому имеет значение

l Ll e2me , (29.25)

где l и Ll – соответственно магнитный и механический момент. К аналогичному результату приводит и квантовая механика. Так как проекция орбитального момента на некоторое

393

направление может принимать только дискретные значения, то это же относится и к магнитному моменту. Поэтому, проекция магнитного момента на направление вектора B при заданном значении орбитального квантового числа l может принимать значения

Bm (m 0, 1,..., l) ,

где B e 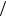2m – так называемый магнетон Бора.

Опыт Штерна и Герлаха. Оптические эксперименты дают вполне достаточные доказательства квантования энергии атомов. Другой вид квантования - пространственное квантование, утверждающее дискретность проекции магнитного момента атома на направление внешнего магнитного поля, демонстрируется экспериментом с атомными пучками, выполненным О.Штерном и В.Герлахом в 1922 г.

Для атома водорода пространственное квантование орбитального магнитного момента описывается форму-

лой Ll l(l 1) . Для более сложных многоэлектронных

атомов эта формула несколько видоизменяется, однако и для таких атомов остается в силе основной вывод квантовой теории: проекция магнитного момента атома на направление внешнего магнитного поля может иметь только дискретные квантовые значения.

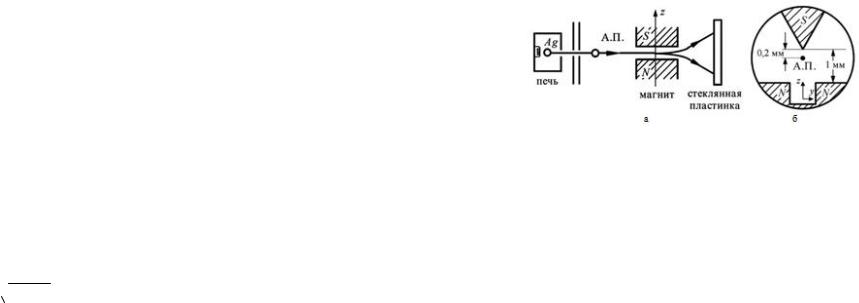
В опыте Штерна и Герлаха пространственное квантование для атомных систем демонстрируется следующим образом. Путем испарения в вакуумной печи атомов серебра или другого металла с помощью тонких щелей формируется узкий атомный пучок (А.П. на рис. 29.17а).

Этот пучок пропускается через неоднородное магнитное поле с существенным градиентом магнитной индукции. Индук-

ция магнитного поля B в опыте велика и направлена вдоль оси

Z .

Для создания такого магнитного поля используется магнит с ножевидным полюсным наконечником (рис. 29.17б), вблизи которого на достаточно малом расстоянии пропускается атомный пучок.

394

Рис. 29.17. Схема опыта Штерна и Герлаха.

На пролетающие в зазоре магнита атомы вдоль направления магнитного поля действует сила

обусловленная градиентом индукции неоднородного магнитного поля и зависящая от величины проекции магнитного момента атома на направление поля. Эта сила отклоняет движущийся атом в направлении оси Z , причем за время пролета магнита движущийся атом отклоняется тем больше, чем больше величина силы (29.26). При этом одни атомы отклоняются вверх, а другие вниз.

С позиций классической физики, магнитный момент атомов вследствие их хаотичного теплового движения, при влете в магнитное поле может иметь любое направление в пространстве. Это соответствует непрерывному распределению значений FZ для различных атомов и, соответственно, любым различным отклонениям атомов. В результате, пролетевшие через магнит атомы серебра должны были образовать сплошную широкую зеркальную полосу на стеклянной пластинке.

Если же, как предсказывает квантовая теория, имеет место пространственное квантование, и проекция магнитного мо-

мента pMZ атома принимает только определенные дискретные значения, то под действием силы (29.26) атомный пучок должен расщепиться на дискретное число пучков, которые, оседая на стеклянной пластинке, дают серию узких дискретных зеркальных полосок из напыленных атомов. Именно этот результат наблюдался в эксперименте.

395

Таким образом, опыт Штерна и Герлаха доказал правильность выводов квантовой теории о наличии пространственного квантования магнитных моментов атомов.

Однако Штерн и В. Герлах в своих опытах проводили прямые измерения магнитных моментов. Они обнаружили, что узкий пучок атомов водорода, заведомо находящихся в s- состоянии, в неоднородном магнитном поле расщепляется на два пучка. В этом состоянии момент импульса, а с ним и магнитный момент электрона равен нулю. Таким образом, магнитное поле не должно оказывать влияние на движение атомов водорода, т.е. расщепления быть не должно.

Для объяснения этого и других явлений Гаудсмит и Уленбек выдвинули предположение, что электрон обладает собственным моментом импульса Ls , не связанным с движением

электрона в пространстве. Этот собственный момент был назван спином.

Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Согласно этим представлениям для отношения магнитного и механического моментов должно выполняться соотношение (29.25). Экспериментально было установлено, что это отношение в действительности в два раза больше, чем для орбитальных моментов

s 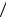Ls e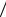me (29.27).

По этой причине, представление электрона как о вращающемся шарике оказывается несостоятельным. В квантовой механике спин электрона (и всех других микрочастиц) рассматривается как внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.

Величина собственного момента импульса микрочастицы определяется в квантовой механике с помощью спинового

мать квантованные значения, отличающиеся друг от друга на . Для электрона

396

Lsz ms (ms s 12) , (29.29)

где ms – магнитное спиновое квантовое число.

Для полного описания электрона в атоме, таким образом, необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.

Принцип тождественность частиц. В классической ме-

ханике одинаковые частицы (скажем, электроны), несмотря на тождественность их физических свойств, можно пометить, пронумеровав, и в этом смысле считать частицы различимыми. В квантовой механике ситуация кардинально меняется. Понятие траектории теряет смысл, и, следовательно, при движении частицы перепутываются. Это означает, что нельзя сказать, какой из первоначально помеченных электронов попал в ту или иную точку.

Таким образом, в квантовой механике одинаковые частицы полностью теряют свою индивидуальность и становятся неразличимыми. Это утверждение или, как говорят, принцип неразличимости одинаковых частиц имеет важные следствия.

Рассмотрим систему, состоящую из двух одинаковых частиц. В силу их тождественности состояния системы, получающиеся друг из друга перестановкой обеих частиц должны быть физически полностью эквивалентными. На языке квантовой механики это означает, что

(29.30)

где 1 , 2 – совокупности пространственных и спиновых координат первой и второй частицы. В итоге возможны два случая

(29.31).

Таким образом, волновая функция либо симметрична (не меняется при перестановки частиц), либо антисимметрична (т.е. при перестановке меняет знак). Оба этих случая встречаются в природе.

Релятивистская квантовая механика устанавливает, что симметрия или антисимметрия волновых функций определяется спином частиц. Частицы с полуцелым спином (электроны, протоны, нейтроны) описываются антисимметричными волновыми

397

функциями. Такие частицы называют фермионами, и говорят, что они подчиняются статистике Ферми-Дирака. Частицы с нулевым или целочисленным спином (например, фотоны) описываются симметричными волновыми функциями. Эти частицы называют бозонами, и говорят, что они подчиняются статистике Бозе-Эйнштейна. Сложные частицы (например, атомные ядра), состоящие из нечетного числа фермионов, являются фермионами (суммарный спин – полуцелый), а из четного – бозонами (суммарный спин целый).

Принцип Паули. Атомные оболочки. Если тожде-

ственные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Отсюда следует, что два фермиона, входящих в эту систему, не могут находиться в одинаковых состояниях, так как для фермионов волновая функция должна быть антисимметричной.

Из этого положения вытекает принцип запрета Паули: любые два фермиона не могут одновременно находиться в одном и том же состоянии.

Состояние электрона в атоме определяется набором четырех квантовых чисел:

Распределение электронов в атоме по состояниям подчиняется принципу Паули, поэтому два электрона, находящихся атоме, различаются значениями, по крайней мере, одного квантового числа.

Определенному значению n соответствует n2 различных состояний, отличающихся l и ml . Так как ms может при-

398

нимать лишь два значения ( 12 ), то максимальное число элек-

тронов, находящихся в состояниях с данным n, будет равно 2n2

. Совокупность электронов в многоэлектронном атоме, имеющих одно и то же квантовое число n, называют электронной оболочкой. В каждой электроны распределяются по подоболочкам, соответствующих данному l. Максимальное число электронов в подоболочке с данным l равно 2(2l 1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в таблице.

Периодическая система элементов Менделеева. С по-

мощью принципа Паули можно объяснить Периодическую систему элементов. Химические и некоторые физические свойства элементов определяются внешними валентными электронами.

Поэтому периодичность свойств химических элементов непосредственно связана с характером заполнения электронных оболочек в атоме.

Элементы таблице отличаются друг от друга зарядом ядра и количеством электронов. При переходе к соседнему элементу последние увеличиваются на единицу. Электроны заполняют уровни так, чтобы энергия атома была минимальной..

В многоэлектронном атоме каждый отдельный электрон движется в поле, которое отличается от кулоновского. Это приводит к тому, что вырождение по орбитальному моменту снимается E Enl . Причем c увеличением l энергия уровней с одинаковыми n возрастает. Когда число электронов невелико, отличие в энергии с различными l и одинаковыми n не так велико, как между состояниями с различными n. Поэтому, сначала электроны заполняют оболочки с меньшими n, начиная с s подоболочки, последовательно переходя к большим значениям l.

Единственный электрон атома водорода находится в состоянии 1s. Оба электрона атома He находятся в состоянии 1s с антипараллельными ориентациями спина. На атоме гелия заканчивается заполнение K-оболочки, что соответствует завершению I периода таблицы Менделеева.

Третий электрон атома Li (Z 3) занимает наинизшее свободное энергетическое состояние с n 2 (L-оболочка), т.е. 2sсостояние. Так как он слабее других электронов связан с ядром атома, то им определяются оптические и химические свойства атома. Процесс заполнения электронов во втором периоде не

400

нарушается. Заканчивается период неоном, у которого L- оболочка целиком заполнена.

В третьем периоде начинается заполнение M-оболочки. Одиннадцатый электрон первого элемента данного периода Na (Z 11) занимает наинизшее свободное состояние 3s. 3s-электрон является единственным валентным электроном. В связи с этим оптические и химические свойства натрия подобны свойствам лития. У следующих за натрием элементов нормально заполняются подоболочки 3s и 3p.

Впервые нарушение обычной последовательности заполнения уровней происходит у K (Z 19). Его девятнадцатый электрон должен был бы занять 3d-состояние в M-оболочке.

При данной общей конфигурации подоболочка 4s оказывается энергетически ниже подоболочки 3d. В связи с чем, при незавершенном в целом заполнении оболочки M начинается заполнение оболочки N. В оптическом и химическом отношении атом K подобен атомам Li и Na. Все эти элементы имеют валентный электрон в s-состоянии.

С аналогичными отступлениями от обычной последовательности, повторяющимися время от времени, осуществляется застройка электронных уровней всех атомов. При этом периодически повторяются сходные конфигурации внешних (валентных) электронов (например, 1s, 2s, 3s и т.д.), чем обуславливается повторяемость химических и оптических свойств атомов.