Курс лекций Оптическая физика

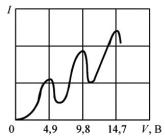
361

С и анод А. Термоэлектроны, вылетевшие из катода, ускорялись разностью потенциалов U, приложенной между катодом и сеткой. Между сеткой и анодом создавалось слабое электрическое поле (разность потенциалов порядка 0,5 В), тормозившее движение электронов к аноду. В опыте исследовалась зависимость силы тока I в цепи анода от напряжения U между катодом и сеткой. Характерная для таких опытов вольтамперная характеристика приведена на рис. 28.4.

Ход кривой можно объяснить следующим образом. При столкновении электрона с атомами ртути возможно взаимодей-

ствие двух типов: 1) упругое столкновение, в результате ко-

торого энергия электронов практически не изменяется, изменяется только направление движения; 2) неупругое столкновение электрона с атомом ртути. При этом энергия электронов уменьшается, за счет передачи ее атому ртути.

В соответствии с постулатами Бора атом ртути может поглотить энергию в виде порции E и перейти в возбужденное состояние на выше расположенный энергетический уровень. Первому возбужденному состоянию атома ртути соответствует энергия 4,9 эВ. При U < 4,9 В электроны испытывают только упругое взаимодействие с атомами ртути и, поэтому, с увеличением напряжения анодный ток возрастает.

Рис. 28.4. Зависимость силы тока I в цепи анода

от напряжения U между катодом и сеткой.

При достижении U 4,9 В энергия электронов сравнивается с энергией первого возбужденного уровня атома ртути. Происходят неупругие столкновения электронов с атомами ртути, которые получают порцию энергии E 4,9 эВ и переходят в возбужденное состояние. Электрон, потерявший энер-

362

гию, не может преодолеть задерживающий потенциал. Поэтому при U 4,9 В происходит уменьшение анодного тока. Аналогичное явление наблюдается при U 2÷4,9 В, U 3÷4,9 В и т.д., когда электроны могут испытывать два, три и т.д. неупругих столкновений с атомами ртути. Потеряв всю (или почти всю) энергию, электрон не сможет достичь анода, задерживающее поле отбросит его к сетке. В результате наблюдается падение тока при этих напряжениях и общий пилообразный ход вольтамперной характеристики.

Атомы паров ртути, получив энергию от электронов, переходят в возбужденное состояние, из которого спустя 10–8 с самопроизвольно возвращаются в основное состояние. При этом должен излучается фотон с длинной волны 255 нм. В опыте действительно обнаруживается одна ультрафиолетовая линия с такой длиной волны. Таким образом, опыты Франка и Герца экспериментально подтверждают постулаты Бора.

Теория водородоподобного атома по Бору. Постулаты Бора позволяют рассчитать спектр атома водорода и водородоподобных ионов, состоящих из ядра Ze и одного электрона, и теоретически вычислить постоянную Ридберга.

Рассмотрим движение электрона в поле атомного ядра. Уравнение движения электрона имеет вид

Исключив v из уравнений L=mvr=ħn (n=1,2…) и (28.5), получим выражение для радиусов допустимых орбит

Для атома водорода (Z 1) радиус первой орбиты называется боровским радиусом. Его значение равно

Полная энергия электрона в водородоподобном атоме складывается из его кинетической энергии и потенциальной энергии взаимодействия с ядром

363

(при ее получении использована формула (28.5)). Учитывая квантование радиусов (28.6), получим, что энергия электрона принимает дискретные значения

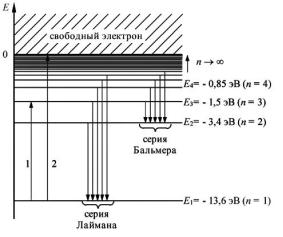
Согласно второму постулату Бора при переходе атома водорода из состояния n в состояние m излучается фотон (рис. 28.5)

Рис. 28.5. Схема энергетических уровней атома водорода.

откуда частота излучения

Таким образом, теория Бора приводит к обобщенной формуле Бальмера, причем для постоянной Ридберга получи-

лось значение R mee4 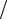(32 2 3 20 ). При подстановке в это

выражение значений универсальных постоянных получается величина, превосходно согласующаяся с экспериментальным значением постоянной Ридберга.

Теория Бора была крупным шагом в развитии теории атома. Она отчетливо показала, что процессы в микромире описываются не классическими, а иными, квантовыми законами.

Элементы квантовой механики.

Волновые свойства вещества. В результате развития представлений о природе света выяснился его двойственный характер (дуализм). Одни явления могут быть объяснены в предположении, согласно которому свет представляет собой поток частиц – фотонов (фотоэффект, эффект Комптона). Другие – в предположении, согласно которому свет является волной (интерференция, дифракция).

В 1924 г. Луи де Бройль, предполагая наличие в природе симметрии, выдвинул гипотезу, что дуализм не является особенностью одного света, что он свойственен всей материи (электронам и любым другим частицам). Согласно де Бройлю, с каждой микрочастицей связывается, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны – волновые характеристики – частота и волновой вектор k ( k 2 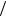). Количественные соотношения, связывающие корпускулярные и волновые характеристики, принимаются для частиц такими же, как для фотонов

E , p k . (28.11)

Гипотеза де Бройля вскоре была подтверждена экспериментально. Дэвиссон и Джермер исследовали в 1927 г. отражение электронов от монокристалла никеля, принадлежащего к кубической системе. Рассеяние электронов проявляет отчетливый дифракционный характер. Положение дифракционных максимумов соответствовало формуле Вульфа-Брегга.

365

В дальнейшем идея де Бройля была подтверждена опытами Г. Томсона и П.С. Тартаковского. В опытах пучок электронов, ускоренный электрическим полем, проходил через тонкую металлическую фольгу и попадал на фотопластинку. Получен ная таким образом картина сопоставлялась с полученной в аналогичных условиях рентгенограммой. В результате было установлено полное сходство двух картин.

Так как дифракционная картина исследовалась для потока электронов, необходимо было доказать, что волновые свойства связаны с электроном, а не являются коллективным эффектом. Это экспериментально установил В.А. Фабрикант. Он показал, что и в случае слабого электрического пучка, когда каждый электрон проходит прибор поодиночке, дифракционная картина при достаточной экспозиции ничем не отличается от картины, какая наблюдается при обычной интенсивности пучка.

Гипотеза де Бройля и ее экспериментальное подтверждение требует качественно нового взгляда на природу микро-

частиц – микрочастицу нельзя считать ни частицей, ни вол-

ной в классическом понимании. Необычные свойства микрочастиц можно понять, если предположить, что вакуум является особым состоянием материи, а микрочастицы ее относительно неустойчивыми локальными состояниями. Не-

устойчивым в том смысле, что микрочастица регулярно растворяется в вакууме и через мгновенье вновь возникает где-то рядом. Аналогией вакууму может служить насыщенный раствор какого-либо вещества, а микрочастице имеющиеся в растворе кристаллики этого вещества. В состоянии динамического равновесия кристаллики в растворе хаотично растворяются и возникают. На характер растворения-возникновения микрочастицы влияет ее окружение. Несмотря на сложность и элемент случайности всего происходящего, поведение микрочастицы, как выяснится позже, можно успешно описать с помощью так называемой волновой функции.

Принцип неопределенности. В классической механике состояние материальной точки определяется заданием значений координат, импульса, энергии и т.д. Перечисленные величины называются динамическими переменными. Так как микрочастица не является частицей в классическом понимании, то ей, стро-

366

го говоря, не могут быть приписаны указанные динамические переменные.

Данное обстоятельство проявляется в том, что не для всех переменных получаются при измерениях определенные значения. Так, например, электрон не может иметь одновременно точных значений координаты x и компоненты импульса px .

Неопределенности значений x и px удовлетворяют соотношению

x px . (28.12)

Соотношение, аналогичное (28.12), имеет место и для y и py ,

для z и pz , а также для ряда других пар величин (называемых канонически сопряженными). Соотношение (28.12) и подобные ему называются соотношением неопределенностей Гейзенберга. Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей

E t . (28.13)

Это соотношение означает, что если время перехода системы из одного состояния в другое характеризуется временем t, то неопределенность энергии системы равна E ~ 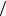t . Процесс измерения энергии сопровождается изменением состояния. Поэтому, неопределенность результата измерения E связана с длительностью измерения t (т.е. временем перехода системы из одного состояния в другое) соотношением (28.13).

Соотношение неопределенностей вытекает из волновых свойств микрочастиц (строгий формальный расчет лежит вне рамок данного курса). Поясним его на следующем примере.

Пусть поток электронов проходит через узкую щель шириной x, расположенную перпендикулярно к направлению их движения (рис. 28.6). При прохождении электронов за щелью наблюдается дифракционная картина, как в случае плоской световой волны. Основная доля электронов приходится на область центрального максимума.

367

Рис. 28.6. Иллюстрация принципа неопределенности. До прохождения электроны двигались вдоль оси y, по-

этому px 0, а координата являлась совершенно неопределенной. Прохождение щели сопровождается изменением состояния электрона. В новом состоянии неопределенность положения по оси x задается шириной щели. Вследствие дифракции частица будет обладать импульсом, распределенным с близкими вероятностями в пределах угла 2 , где – угол, соответствующий первому дифракционному минимуму. Таким образом, появляется неопределенность

px psin .

Первому минимуму при дифракции от щели соответствуют угол, для которого

x sin ,

где длина волны де Бройля. Отсюда с учетом (28.11) получается соотношение

x px ~ 2

согласующееся с (28.12).

Строгий вывод соотношения неопределенностей, сделанный в 1927 г. Гейзенбергом дает следующую формулу:

368

2

Основные понятия квантовой механики. Эксперимен-

тальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового дуализма стимулировали развитие квантовой теории, которое привело к созданию законченной теории.

Прежде всего, следует дать физическую интерпретацию волн де Бройля. С этой целью сравним дифракцию световых волн и микрочастиц. Дифракционная картина световых волн образуется в результате интерференции вторичных волн. В свете волновых представлений, интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны. По представлениям корпускулярной теории, интенсивность определяется числом фотонов, попадающих в данную точку дифракционной картины. Если принять, что число фотонов в данном месте (а для одного фотона вероятность обнаружения) пропорционально квадрату светового вектора, то два способа описания становятся согласованными и дополняющими друг друга.

Дифракционная картина для микрочастиц имеет сходный вид с дифракционной картиной световых волн. Наличие максимумов с точки зрения волновой теории соответствуют наибольшей интенсивности волн де Бройля. Интенсивность волн де Бройля коррелирует с числом частиц в данной точке пространства. Таким образом, напрашивается вероятностная, как для световых волн, трактовка волн де Бройля: вероятность обнаружения микрочастицы пропорциональна интенсивности волны де Бройля (квадрату модуля волновой функции).

369

Необходимость вероятностного подхода к описанию микрочастиц является принципиальным положением квантовой теории. Постулируется, что состояние квантовой системы может быть максимально полно описано с помощью волновой функции, в общем случае комплексной. В случае микрочастицы, не имеющей внутренних степеней свободы, эта функция имеет вид(t,x,y,z). Вероятность dP обнаружения микрочастицы в пределах объема dV

dP ~ | |2 dV * dV.

В квантовой механике принимается, что волновые функции, отличающиеся только множителем, описывают одно и то же состояние. Это обстоятельство позволяет ввести условие нормировки на пси-функцию

* dV 1. .

Для нормированной пси-функции квадрат ее модуля дает плотность вероятности нахождения частицы в соответствующем месте пространства

dP | |2 dV * dV .

По своему смыслу, волновая функция должна удовлетворять ряду так называемых стандартных условий. Она должна быть однозначной, непрерывной (вероятность не может изменяться скачком), конечной (требование условия нормировки). Подобные условия накладываются и на производные волновой функции.

Одним из основных положений квантовой механики является принцип суперпозиции состояний. Если система может находиться в состояниях, описываемых волновыми функциями1 , 2 , …, n , то она также может находиться в состоянии

где Cn – произвольные комплексные числа.

Волновая функция содержит в себе полную информацию о микрообъекте. Поэтому, зная , можно вычислить вероятности значений, которые получаются при измерении какойлибо физической величины (а значит и их средние) в этом со-

370

стоянии. Например, среднее значение координаты x вычисляется по формуле

В квантовой механике принимается, что измерение физической величины q даст некоторое значение qn . Совокуп-

ность или спектр возможных значений qn называются собственными значениями величины q. Обозначим волновую функцию системы в состоянии, в котором величина q всегда имеет определенное значение qn , через n . Волновые функции

n называются собственными функциями данной величины q. Каждая из этих функций предполагается нормированной

.

Если система находится в некотором произвольном состоянии с волновой функцией , то в соответствии с принципом суперпозиции, она должна представлять собой комбинацию собственных функций в виде (28.14). Утверждается, что квадраты модулей Cn дают вероятности того, что при измерении бу-

дет получено соответствующее значение величины qn . Последовательно рассуждая, можно установить, что собственные функции взаимно ортогональны

m* n dV mn .

Зная вероятности различных значений величины q, ее среднее значение в состоянии вычисляется по формуле

q |Cn |2 qn .

n

В квантовой механике вводится понятие оператора. Так называется математическая операция, с помощью которой одной функции ставится в соответствие другая

Q ,

где Q – символическое обозначение операции (оператора). Оператор физической величины определяется посредством соотношений

371

(для всех n),

где qn –собственное значение q. Свойство ортогональности собственных функций позволяет записать

.

Формула (28.15) является выражением такого типа. Можно до-

казать, что оператор Q является эрмитовым

*Q dV (Q )* dV .

Уравнение Шредингера. Состояние микрообъекта или какой-либо квантово-механической системы в результате внутренних и внешних взаимодействий с течением временем меняется. Это символически можно выразить с помощью оператора эволюции

(28.16)

При t 0 ничего не должно произойти, так как мы вправе ожидать плавных изменений. Таким образом U(t,t) 1. Кроме того, можно предположить, что при малых t U(t t,t) отличается от единичного оператора на величину, пропорциональную t, так что можно записать

Множитель i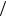 выделяется в (28.17) по историческим причи-

нам. Подставляя в (28.16) этот вид U(t t,t) приходим к операторному уравнению

i H .(28.18)

t

Оператор H носит название гамильтониана системы. В соответствии со своим смыслом, нормировка волновой функции не меняется со временем. Исходя из этого, можно показать, что гамильтониан является эрмитовым оператором. Возникает задача определения гамильтониана.

372

Для начала рассмотрим свободно движущуюся частицу,

имеющей импульс p и энергию E p2 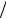2m . Согласно де Брой-

лю ей сопоставляется плоская волна Aei( t kx) . Если учесть, чтоE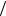 и k p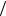 , то волновая функция частицы выглядит как

Ae (i )(Et px) . (28.19)

В квантовой механике показатель экспоненты берут со знаком минус. Поскольку физический смысл имеет только | |2, то это оказывается несущественным. Из данного вида волновой функции можно получить соотношения

Откуда, используя связь между энергией и импульсом частицы, получим уравнение

Если частица движется в силовом поле, обладающем по-

тенциальной энергией U, то полная энергия E p2 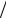2m U. Проводя аналогичные рассуждения, приходим к уравнению Шредингера

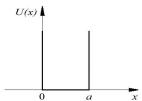
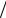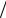где – оператор Лапласа ( 2 x2 2 y2 2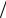 z2 ). Приведенные рассуждения не есть вывод уравнения Шредингера. Они поясняют, каким путем уравнение могло быть получено. Уравнение Шредингера, как основное уравнение нерелятивистской квантовой механики, постулируется.

Уравнение (28.20) является общим уравнением Шредингера. Если силовое поле, в котором движется частица, стационарно U U(x,y,z), то в этом случае решение уравнения Шредингера распадается на два множителя

(t,x,y,z) (x,y,z)e i(E )t ,

где E имеет смысл полной энергии частицы. Подставив это вы-

373

ражение в (28.20) и после несложных преобразований, придем к дифференциальному уравнению для

Уравнение (28.21) называется уравнением Шредингера для стационарных состояний (или просто уравнением Шредингера).

Уравнение Шредингера позволяет найти пси-функцию данного состояния и, следовательно, получить полную информацию о системе. В уравнение (28.21) в качестве параметра входит полная энергия E частицы. В теории дифференциальных уравнений доказывается, что уравнения вида (28.21) имеют решения, удовлетворяющие стандартным и граничным условиям, не при любых значениях параметра, а лишь для некоторых из них. Эти значения называются собственными значениями гамильтониана (энергии). Решения, соответствующие собственным значениям E, называются собственными функциями гамильтониана.

Таким образом, квантование энергии является следствием основных положений квантовой механики. Нахождение собственных значений и собственных функций, как правило, является нетривиальной математической задачей.

374

Лекция 29

Потенциальная яма с бесконечно высокими стенками Туннельный эффект Гармонический осциллятор Атом водорода

Квантовые числа и их физический смысл Правило отбора

Вырожденные состояния Спин электрона

Принцип тождественность частиц Принцип Паули. Атомные оболочки Таблица Менделеева

Потенциальная яма с бесконечно высокими стенка-

ми. Рассмотрим одномерный случай. Потенциальная энергия имеет вид

, x 0,

U(x) 0, 0 x a,

, x a,

где a– ширина ямы, а энергия отсчитывается от ее дна.

Рис. 29.1. Потенциальная яма с бесконечно высокими стенками.

Уравнение Шредингера для стационарных состояний запишется в виде

375

ния за пределами ямы равна нулю. Следовательно, на границах ямы волновая функция должна обращаться в ноль

(0) (a) 0 . (29.2)

В пределах ямы (0 x a ) уравнение Шредингера сводится к уравнению

Общее решение уравнения (29.3) имеет вид

(x) Asin(kx ) ,

где k2 2mE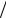 2 , A и – произвольные постоянные.

Граничные условия (29.2) будут выполнены при 0 и

ka n , где n – целое число. Отсюда следует, что энергия частицы принимает квантованные значения

Значения энергии En называются уровнями энергии, а число n, определяющее энергетические уровни частицы, называется главным квантовым числом.

Рис. 29.2. Возможные значения полной энергии частицы. Поскольку частица в потенциальной яме находится в

связанном состоянии то можно сделать вывод. В связанном со-

стоянии частица обладает дискретным спектром энергий.

Следует отметить, что минимальное значение энергии частицы, находящейся в основном состоянии, отлично от нуля. Этот результат согласуется с соотношением неопределенностей и является общим для всех задач квантовой механики. В классической механике минимальную энергию, равную нулю, имеет покоящаяся в яме частица. Такого состояния покоя у квантовой

376

частицы не существует. Обсудим подробнее вопрос о дискретности энергетического спектра. Разность энергий n -го и n+1-го энергетических уровней ∆En равна

молекулу газа массой m0 ≈ 10-27 кг в сосуде размером a ≈ 0,1 м.

При этом ∆En ≈ 6,8·10-20·n эВ.

Энергетическое расстояние между соседними уровнями оказывается столь малым по сравнению с энергией теплового хаотического движения молекулы kT (при комнатной температуре kT ≈ 2,6·10-2 эВ), что практически можно говорить о сплошном энергетическом спектре движущейся молекулы.

Собственные волновые функции частицы имеют вид

Рис. 29.3. Вид волновых функций соответствующих разным энергетическим уровням.

377

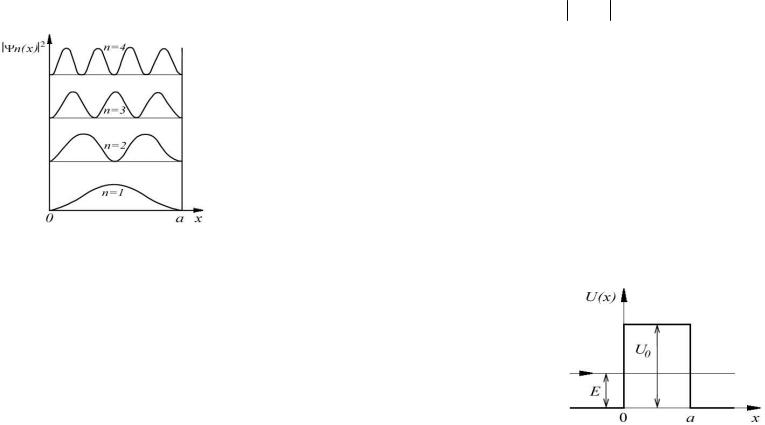
На рис. 29.4 представлены графики квадрата модуля волновой функции |Ψn(x)|2 , определяющего плотность вероятности нахождения частицы в яме.

Рис. 29.4. Графики квадрата модуля волновой функции |Ψn(x)|2 , определяющего плотность вероятности нахождения частицы в яме.

Плотность вероятности оказывается существенно различной для разных состояний частицы, т.е. для разных значений квантового числа n. Так, например, в основном состоянии, т.е.

при n = 1 , частица с наибольшей вероятностью находится в центре ямы, а в первом возбужденном состоянии, т.е. при n = 2 , вероятность обнаружить частицу в центре ямы равна нулю, хотя пребывание частицы в левой и правой половинах ямы равновероятно. Такое поведение кардинально отличается от поведения в яме классической частицы, для которой плотность вероятности нахождения частицы одинакова в любой точке ямы.

С увеличением же энергии (т. е. с ростом квантового числа п) максимумы распределения ψ2n(х) располагаются все ближе друг к другу. При очень больших значениях п картина распределения ψ2n(х) практически «сливается» и представляется равномерным — частица начинает вести себя совсем «как классическая».

Вероятность того, что частица в яме находится в области x1 ≤x ≤ x2 , определяется выражением

378

x2 2

P n (x) dx

x1

Отметим, что с математической точки зрения задача о движении частицы в одномерной потенциальной яме с непроницаемыми стенками аналогична задаче о колебании струны с закрепленными концами. И в том, и в другом случае из граничных условий следует, что на ширине ямы (на длине струны) должно укладываться целое число полуволн a = n·(λ/2) . В нашем случае λ - это дебройлевская длина волны частицы в яме .

Туннельный эффект. Рассмотрим потенциальный барьер прямоугольной формы для одномерного (по оси x) движения частицы

, x 0,

U(x) U, 0 x a,

, x a,

Рис. 29.5. Потенциальный барьер прямоугольной формы для одномерного (по оси x) движения частицы

Классическая частица, обладая энергией E, либо беспрепятственно пройдет над барьером (при E U ), либо отразится от него (при E U), т.е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при E U , имеется отличная от нуля вероятность отразиться от барьера. При E U имеется также отличная от нуля вероятность прохождения частицей барьера. Подобные выводы следуют из решения уравнения Шредингера.

379

Уравнение Шредингера для стационарных состояний для каждой из выделенной на рис. области имеет вид

В выражениях для областей 1 и 3 (k – действительное число) первый член представляет собой правую плоскую волну (соответствует частице, движущейся в положительном направлении x), а второй – левую волну (соответствует частице, движущейся в отрицательном направлении x). Коэффициент B3

следует положить равным нулю, поскольку из физического смысла в области 3 имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Интерес представляет случай, когда полная энергия частицы меньше высоты барьера, поскольку при E U законы классической физики не разрешают частице проникнуть через барьер. В этом случае

q i , где 2m(E U)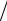 , является чисто мнимым чис-

лом.

Качественный характер функций ψ1(x), ψ2(x) и ψ3(x) иллюстрируется на рис. откуда следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. Следовательно, получили, что частица имеет отличную от нуля вероятность прохождения сквозь потенциальный барьер конечной ширины.

Туннельный эффект — специфически квантовое явление, не имеющее аналога в классической физике (где такого в принципе не может быть). Этим эффектом объясняются многие

380

физические явления; например, холодная эмиссия электронов из металлов, альфа-распад, спонтанное деление ядер и др.

Рис. 29.6. Поведение волновой функции вне и внутри потенциального барьера.

Для описания туннельного эффекта вводится понятие коэффициента прозрачности D потенциального барьера. Он равен отношению плотности потока прошедших частиц к плотности потока падающих

D | A3 |2 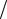| A1 |2 .

Условие непрерывности волновой функции и ее производных позволяют найти связь между коэффициентами в уравнениях (29.6а)-(29.6в) и определить коэффициент прозрачности. Для малых значений коэффициента получается зависимость

где D0 – постоянный множитель, близкий к единице.

Для потенциального барьера произвольной формы, в квазиклассическом приближении (достаточно плавный профиль потенциальной кривой), получается подобная (29.7) формула