Курс лекций Оптическая физика

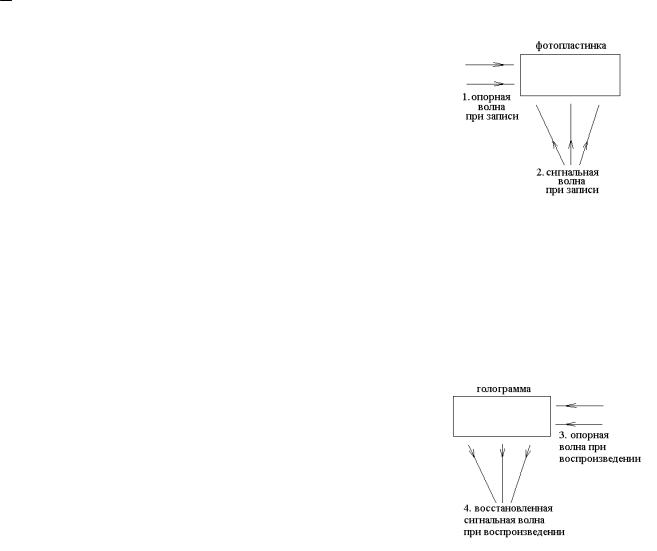
321

частоты на величину порядка v , где v - скорость звука, а с c

– скорость света, можно не принимать во внимание). эксперимент, осуществленный впервые С.А. Ахмановым и Р.В. Хохловым, можно по научной значимости сравнить с первым наблюдением голографических картин. По образному выражению Р.В. Хохлова, «кювету с рассеивающим веществом можно рассматривать как волшебное зеркало, изменяющее знак времени». Эффект обращения волнового фронта уточняет представления о необратимых и обратимых оптических явлениях. Информация о первоначальной структуре когерентного светового пучка не те-

ряется при прохождении через фазовую пластинку. Меха-

низм вынужденного рассеяния обращает искаженный волновой фронт с сохранением этой информации. При прохождении в обратном направлении через ту же пластинку все внесенные ею искажения волнового фронта полностью компенсируются, и пучок восстанавливает свою структуру, т.е. возвращается в ис-

ходное состояние, но обращенное во времени.

С помощью обращения волнового фронта в нелинейной среде можно получить предельно малую расходимость излучения мощных лазеров с оптически неоднородными активными средами. Случайные неоднородности активной среды искажают волновой фронт и ухудшают направленность выходного пучка. Воспользуемся описанным явлением для ликвидации этого ухудшения. Именно, пропустим пучок от задающего маломощного лазера через мощный оптический усилитель с такой слу- чайно-неоднородной средой. После обращения волнового фронта в нелинейной среде излучение вновь пропустим через тот же усилитель в противоположном направлении. При этом одновременно с дальнейшим увеличением интенсивности происходит компенсация искажений волнового фронта, и выходящее излучение имеет направленность, аналогичную направленности пучка от задающего лазера (а в силу маломощности этот пучок легко сделать минимально, т.е. дифракционно расходящимся). Таким методом были получены рекордные по фокусировке в предельно малом объеме результаты концентрации мощного излучения.

322

Динамическая голография или четырехволновое взаимодействие.

Рассмотрим запись толстослойной голограммы.

Рис. 26.5. Запись толстослойной голограммы. Обернем во времени картину распространения обеих

световых волн опорной и сигнальной. Интерференционная картина в среде фотопластинки при этом не изменится, так как в каждой точке среды сохранится модуль разности фаз интерферирующих волн. Следовательно, ту же голограмму можно было записать с обеими волнами в обратных направлениях.

При воспроизведении голограммы направим опорную волну во встречном направлении, тогда и восстановленная сигнальная волна изменит направление на противоположное.

Рис. 26.6. Воспроизведение толстослойной голограммы. Если при записи голограммы была расходящаяся сиг-

нальная волна, то при воспроизведении получится сходящаяся

323

волна. При воспроизведении произошло обращение волнового фронта волны.

В динамической голограмме одновременно присутствуют все четыре рассмотренные волны. По этой причине это явление называют еще четырехволновым взаимодействием. В этом случае запись и воспроизведение голограммы происходит одновременно.

Рис. 26.7. Схема динамической голографии.

Если в обычной голограмме запись происходит с помощью фотоматериала, то в динамической голограмме вместо фотоматериала используется нелинейная оптическая среда.

В любой прозрачной среде в сильном световом поле показатель преломления изменяется. Если среда изотропная, то показатель преломления не изменяется при изменении направ-

ления вещественного поля E на противоположное. В таком случае разложение показателя преломления в ряд Тейлора содержит только четные степени поля E. Обычно, рассматривая зависимость показателя преломления от светового поля, ограничиваются учетом только первой неисчезающей поправки:

nn0 n2 E2 .

Вдинамической голограмме 1-я опорная и 2-я сигнальная световые волны, взаимодействуя с нелинейной средой, изменяют ее показатель преломления в соответствии с объемной интерференционной картиной. В каждом плоском слое нелинейной среды интерференционные полосы изменения показателя преломления образуют фазовую дифракционную решетку.

324

Опорная волна 3 дифрагирует на этой решетке, образуя сигнальную волну 4.

Поскольку все четыре волны присутствуют одновременно, любая из двух сигнальных волн участвует в записи голограммы в паре с любой из двух опорных волн. Происходит взаимная перекачка энергии между волнами. Из термодинамических соображений следует, что интенсивности волн стремятся к выравниванию.

Вынужденное комбинационное рассеяние (ВКР).

Наряду с ВРМБ в начале 60-х годов было открыто явление вы-

нужденного комбинационного рассеяния (ВКР). Аналогично ВРМБ, классический случай комбинационного рассеяния представляет собой появление в спектре рассеянного света линий, сдвинутых относительно частоты падающего излучения ω на частоту собственных колебаний молекул среды Ω. Само по себе происхождение этих линий легко объяснить индуцированными падающим излучением осцилляциями дипольного момента молекул, в результате которых рассеянное излучение оказывается промодулированным по частоте:

где α - поляризуемость среды, меняющаяся по гармоническому закону с частотой Ω при отклонении атомов в молекуле от равновесного положения по тому же закону x(t) acos t, μ =

( x)0 — коэффициент, характеризующий изменение поля-

ризуемости при смещении атомов из равновесного положения, α0 — поляризуемость в равновесной конфигурации.

В квантовых представлениях, стоксова компонента с частотой (ω – Ω) возникает при уменьшении энергии фотона ħω на величину энергии кванта колебаний молекулы ħΩ, антистоксова (ω + Ω) - при передаче энергии кванта первоначально возбужденной молекулы излучению. В классике интенсивность антистоксовой компоненты, пропорциональная числу возбужденных молекул, много меньше интенсивности стоксовой, поскольку соотношение числа возбужденных и невозбужденных молекул в

325

равновесии подчиняется формуле Больцмана exp( kБT) «

1.

ВКР, в отличие от классики, также дает испускание стоксовой и антистоксовой спектральных компонент, но с веро-

ятностью процесса, зависящей от интенсивности падающего излучения. Как и ВРМБ, ВКР возникает только при интенсивности падающего излучения, превышающей некоторую пороговую величину. При этом доля рассеянного излучения достигает десятков процентов (при 10-7 … 10-8 от интенсивности падающего света в классическом случае). Как и полагается при нелинейных взаимодействиях, в рассеянном излучении наблюдаются не только частоты (ω ± Ω), но и (ω ± 2Ω) и т.д. Рассеяние имеет четко выраженный направленный характер. Это объясняется интерференцией вторичных волн, испускаемых диполями в различных точках рассеивающей среды, т.е. опять возникает условие фазового синхронизма.

Для стоксова излучения выполнение условия фазового синхронизма наилучшим образом обеспечивается при совпадении направлений падающего и рассеянного излучения, поскольку при параллельности пучков объем среды, где происходит их наложение, много больше, чем для внеосевого направления. Для антистоксовой компоненты в среде с нормальной дисперсией условие фазового синхронизма наилучшим образом выполняется в направлениях, составляющих небольшой угол с возбуждающим пучком (например, в нитробензоле для излучения рубинового лазера этот угол составлял 30), поэтому при наблюдении ВКР возможно пространственное разделение стоксовой и антистоксовой компонент при сравнимых между собой интенсивностях. Интересно, что исторически ВКР было обнаружено раньше, чем ВРМБ, поскольку оно обычно сопровождается другими нелинейными явлениями, благодаря которым порог наблюдения понижается.

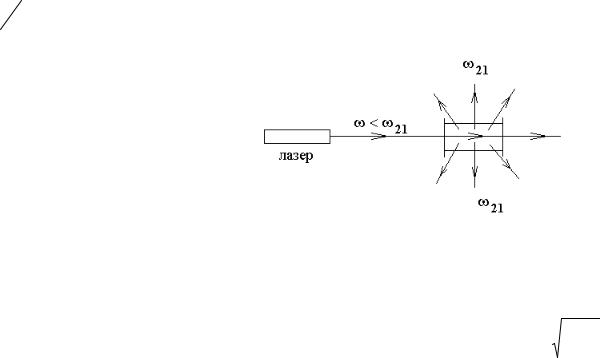
Лазерное охлаждение. Излучение лазера с частотой пропускают через кювету с газом, который имеет линию поглощения 21 . Свет частично поглощается средой, переводя атомы среды в возбужденное состояние. Некоторые атомы возвраща-

326

ются на нижний уровень энергии в результате спонтанного излучения, которое равновероятно происходит по всем направлениям.

Рис. 26.8. Оптическая схема опыта по лазерному охлаждению.

Пусть частота излучения лазера меньше частоты поглощающего перехода среды, но пусть разность частот не велика и имеет порядок доплеровской ширины kU спектральной линии

наиболее вероятная скорость атомов газа.

Если после поглощения кванта света атомом газа безизлучательный переход на другие уровни энергии атома маловероятен, то газ охлаждается.

Рассмотрим два эквивалентных объяснения этого явления: объяснение через рассмотрение импульса и объяснение через рассмотрение энергии.

Рассмотрение через импульс. Свет резонансно погло-

щается атомами, в системе отсчета которых частота света совпадает с частотой поглощающего перехода 21 . С учетом продольного эффекта Доплера частота света в системе отсчета ато-

ма / отличается от частоты света в лабораторной системе отсчета:

/ kVz ,

327

где k 2 — волновое число, Vz — проекция скорости атома

на направление лазерного луча.

Свет резонансно поглощается атомами, для которых

Vz 21 0 k

Проекция скорости атомов на луч отрицательная, так как21 по условию эксперимента. Отрицательная проекция

скорости означает, что поглощающие свет атомы летят навстречу лучу.

Поглощенный фотон имеет импульс

p , c

который переходит к поглощающему свет атому.

При поглощении импульса фотона проекция скорости Vz атома на луч уменьшается по модулю, так как атом летел навстречу поглощенному фотону. Уменьшается импульс атома.

При излучении атом тоже испытывает отдачу от излучаемого фотона, но спонтанное излучение изотропно, поэтому при излучении фотона импульс атома увеличивается и уменьшается равновероятно.

В среднем в результате каждого акта поглощения и спонтанного излучения импульс атома уменьшается. Кинетическая энергия связана с импульсом атома соотношением

E p2 , а энергия связана с температурой E 3 kT. Умень-

2m 2

шение импульса означает уменьшение энергии и охлаждение.

Объяснение лазерного охлаждения через рассмотрение энергии.

По условию эксперимента частота падающего света меньше частоты поглощающего перехода 21 , тогда

328

21 — получаемая атомом энергия падающего фотона меньше энергии, которую атом теряет при спонтанном излучении фотона.

Атом получает меньше энергии при поглощении, чем отдает при излучении. Следовательно, среда теряет энергию и охлаждается.

Рассмотрим этот процесс чуть подробнее.

В своей собственной системе отсчета атом поглощает и излучает свет одной и той же частоты 21 , но в лабораторной системе отсчета частоты оказываются разными.

Поглощают свет атомы, которые летят навстречу лучу. При переходе из лабораторной системы отсчета в систему отсчета атома частота поглощаемого света увеличивается от до21 . Спонтанное излучение света равновероятно по направлениям, поэтому доплеровский сдвиг излучаемого кванта при возвращении в лабораторную систему отсчета равновероятно увеличивает и уменьшает частоту света. В среднем при излучении сдвига частоты нет.

Предел охлаждения определяется тем, что атом при поглощении кванта света может остановиться, испытав отдачу от фотона. Тогда при излучении атом снова испытает отдачу и вернется к прежнему значению скорости. В таком случае охлаждения уже не будет.

Приравняем импульс фотона к импульсу атома

здесь T — предел лазерного охлаждения в Кельвинах, A — вес атома в атомных единицах.

рость при предельном охлаждении, выраженная в метрах в секунду; A — вес атома в атомных единицах.

Дальнейшее охлаждение возможно по принципу открытого стакана с водой. Открытый стакан с водой имеет температуру ниже комнатной температуры, так как только молекулы с наибольшими энергиями способны преодолеть притяжение других молекул воды и вылететь с поверхности воды. При этом для остающихся в стакане молекул средняя энергия уменьшается.

Роль стакана при лазерном охлаждении играет система потенциальных ям. Для создания системы потенциальных ям используются три пары лазеров, которые светят навстречу друг другу по трем осям координат. Каждая пара лазеров создает стоячую световую волну, в пучности которой втягиваются атомы. Излучение лазеров далеко отстоит по частоте от линий поглощения атомов.

Втягивание атомов в пучность светового поля определя-

поль F W E2 . Градиент направлен в сторону увеличения поля E, то есть наведенные диполи втягиваются в световое поле.

Три ортогональные стоячие волны образуют решетку из потенциальных ям. В этих ямах скапливаются охлажденные лазером атомы. В каждой потенциальной яме остается много атомов. Атомы случайным образом сталкиваются, и когда один из них случайно получает достаточно большую энергию, он вылетает из потенциальной ямы. Такие вылетевшие атомы откачиваются насосом. По мере испарения горячих атомов из потенциальных ям оставшиеся атомы становятся все холоднее. Таким образом удается практически остановить атомы в потенциальных ямах и довести их тепловые скорости до единиц миллиметров в секунду.

330

Вопросы:

1.Условие наблюдения нелинейных оптических эффектов?

2.Причина генерации оптических гармоник?

3.Самофокусировка луча причины возникновения?

4.Оптическое гетеродинирование и параметрическое усиление света?

5.Вынужденное рассеяние?

6.Обращение волнового фронта?

7.Динамическая голография или четырехволновое взаимодействие?

8.Вынужденное комбинационное рассеяние?

9.Лазерное охлаждение

331

12. Квантовая оптика

Лекция 27

Тепловое излучение Фотоэффект Фотоны. Давление света Эффект Комптона

Корпускулярно-волновой дуализм электромагнитного излучения Опыт Дэвиссона и Джермера

Квантовой оптикой называют раздел оптики, занимающийся изучением явлений, в которых проявляются квантовые свойства света. К таким явлениям относятся: тепловое излучение, фотоэффект, эффект Комптона, излучение атомов, молекул, твердых тел, вынужденное излучение и, соответственно, физика лазеров и др.

Тепловое излучение.

Первый закон Кирхгофа. Излучение электромагнитных волн (свечение тел) может осуществляться за счет различных видов энергии. Самым распространенным является тепловое излучение, т.е. испускание электромагнитных волн за счет внутренней энергии тел. Все остальные виды свечения, возбуждаемые за счет любого вида энергии, кроме внутренней (тепловой), объединяются под общим названием люминесценция.

Тепловое излучение имеет место при любой температуре, однако, при невысоких температурах излучаются практически лишь длинные (инфракрасные) электромагнитные волны.

Рассмотрим замкнутую полость, стенки которой имеют температуру T (в ней могут находиться другие тела).

Благодаря излучению стенок полость заполнена электромагнитным излучением со всевозможными направлениями распространения, поляризациями и частотами. В равновесном состоянии во всех точках полости устанавливается одинаковая и неизменная плотность энергии излучения u(T), зависящая от температуры T. Более того, стационарность равновесного состояния подразумевает, что в каждой точке полости устанавливает-

332

ся одинаковое распределение энергии по спектру и изотропная направленность излучения, в том числе каждой спектральной составляющей.

Рис. 27.1. Модель теплового равновесного излучения. Это позволяет ввести спектральную плотность энергии

u ( ,T), так что произведение u ( ,T)d дает долю плотно-

сти энергии, приходящейся на интервал частот d . Очевидно, между u(T) и u ( ,T) существует следующая связь

0

Внутренняя энергия излучения связана с объемной плотностью соотношением

U u(T)V . (27.2)

Легко установить, что спектральная (и объемная) плотность энергии не зависит от свойств стенок полости и представляет собой универсальную функцию частоты и температуры (объемная плотность – только температуры). Данное утверждение составляет содержание первого закона Кирхгофа.

Действительно, пусть две такие полости с разными материалами стенок, но одинаковой температурой имеют хотя бы для одной частоты разные спектральные плотности. Тогда соединяя их с помощью отверстия (возможно со встроенным светофильтром), мы получили бы сначала поток энергии от одной полости к другой при равенстве температур, а затем от полости с более низкой температурой к полости с более высокой температурой, что запрещено принципами термодинамики.

333

Второй закон Кирхгофа. Поток энергии, испускаемой единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2 ), называют энергетической светимостью тела R(T), которая зависит от температуры. Излуче-

ние состоит из волн различных частот . Обозначим через

r ( ,T) спектральную плотность энергетической светимости

(испускательная способность) тела, так что произведение

r ( ,T)d дает долю излучаемой энергии, приходящейся на интервал частот d . Очевидно, между R(T) и r ( ,T) суще-

ствует связь следующего вида

Пусть на элементарную площадку поверхности тела падает поток лучистой энергии d , приходящийся на интервал

частот d . Часть этого потока d будет поглощена телом.

Безразмерная величина

называется поглощательной способностью тела (a ( ,T) 1).

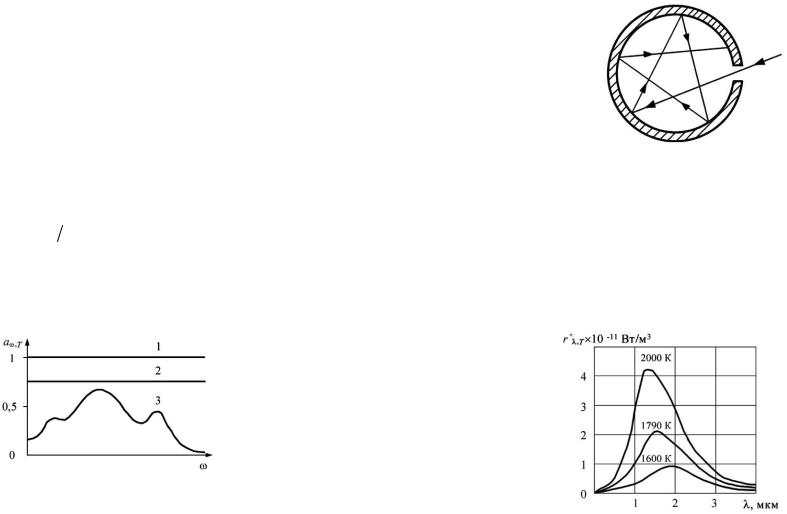
Тело, полностью поглощающее упавшее на него излучение всех частот (a ( ,T) 1) называется абсолютно черным. Тело, для которого a ( ,T) A(T) 1, называют серым.

Рис. 27.2. Поглощательные способности: 1 - абсолютно черное тело; 2 - серое тело; 3 - реальное тело

334

Абсолютно черных тел не существует. Сажа, например, имеет поглощательную способность a ( ,T), близкую к еди-

нице, лишь в очень ограниченном интервале частот; в далекой инфракрасной области ее поглощательная способность заметно меньше единице. Реализовать абсолютно черное тело можно в виде полости с небольшим отверстием (рис. 27.3).

Рис. 27.3. Модель абсолютно черного тела. Лучи попадающие через отверстие внутрь полости, в ре-

зультате многократных отражений на внутренних стенках полости практически полностью поглощаются и не выходят наружу. Это обстоятельство наглядно проявляется, например, при взгляде на открытые окна в доме, которые в светлый день кажутся темными. Высокие поглощающие свойства сажи отчасти объясняются ее пористостью, благодаря чему падающий свет испытывает перед последним отражением несколько промежуточных. Излучение, исходящее из отверстия, в свою очередь, может рассматриваться как излучение абсолютно черного тела.

Рис. 27.4. Зависимость испускательную способности

335

абсолютно черного тела от длины волны.

Обозначим через r* ( ,T) испускательную способность

абсолютно черного тела. Согласно второму закону Кирхгофа между испускательной и поглощательной способностью любого тела существует связь

r ( ,T) r* ( ,T) . (27.5)

Обосновать закон можно исходя из энергетического баланса на поверхности тела между падающим, отраженным и испущенным излучением. Этот баланс должен выполнятся не только в целом, но и в каждом спектральном интервале.

Вследствие изотропии излучения, из каждой точки полости исходит поток энергии, равномерно распределенный и равный в расчете на единицу телесного угла cu ( ,T)4 . На единицу площади поверхности полости за единицу времени под углом к нормали в телесном угле d 2 sin d падает по-

ток энергии (c4 )u ( ,T)cos d . Общее количество пада-

ющей энергии в единичном интервале частот равно.

2

12 cu ( ,T) sin cos d 14 cu ( ,T).

0

В результате отражения падающего излучения и собственного излучения в полость с единичной поверхности тела идет поток энергии

14 cu ( ,T) 1 a ( ,T) r ( ,T) .

Так как тепловое равновесие не должно нарушаться, то между энергией падающего и идущего от поверхности излучения должно выполняться равенство. На этом основании приходим ко второму закону Кирхгофа (27.5) с установлением связи

Закон Стефана-Больцмана. Электромагнитным излучением переносится импульс. Если объемная плотность энергии плоской волны равна u, то объемная плотность импульса

p uc. По этой причине равновесное излучение оказывает

336

давление на стенки полости. Нетрудно установить (подсчитав импульс падающего и уходящего от стенки излучения), что это давление не зависит от материала стенки и равно одной трети плотности энергии излучения

P 13 u(T) . (27.7)

Используя термодинамическое соотношение

и выражения (27.2) и (27.7), приходим к уравнению

4u(T) Tu (T) .

Интегрируя, получаем отсюда для объемной плотности энергии формулу

а для энергетической светимости абсолютно черного тела выражение

Соотношение (27.9) носит название закона Стефана-Больцмана, а константа =5,67·10-8 Вт/(м2К4) – постоянной СтефанаБольцмана.

Для реальных тел закон Стефана-Больцмана выполняется лишь качественно, то есть с ростом температуры энергетические светимости всех тел увеличиваются. Однако, для реальных тел зависимость энергетической светимости от температуры уже не описывается простым соотношением(27.9), а имеет вид

Коэффициент AT в (27.10), всегда меньший единицы, можно назвать интегральной поглощательной способно-

стью тела. Значения AT , в общем случае зависящие от температуры, известны для многих технически важных материалов. Так, в достаточно широком диапазоне температур для металлов AT = 0,1 – 0,4, а для угля и окислов металлов AT = 0,5 – 0,9 .

Закон смещения Вина. Вин теоретически обосновал второй закон черного излучения из общего характера функции

337

r* ( ,T). Он рассмотрел процесс адиабатического сжатия излу-

чения, заключенного внутри идеально зеркального сосуда. Принимая во внимание изменение частоты излучения при отражении от движущегося зеркала (эффект Доплера), Вин пришел к выводу, что испускательная способность черного тела имеет вид

r* ( ,T) 3f( 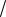T) . (27.10а)

Испускательная способностью r* ( ,T), выраженная в шкале длин волн, связана с r* ( ,T), выраженной в шкале ча-

стот, формулой

(ее легко установить из соотношений r*( ,T)d r* ( ,T)d и

2 c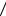 ). Используя формулу (27.10а), находим общий вид функции r* ( ,T)

. (27.10б)

Соотношение (27.10б) позволяет установить зависимость между длиной волны m , на которую приходится максимум

функции r* ( ,T), и температурой. Представим (27.10б) в виде r*( ,T) T5 ( T). Из него с очевидностью вытекают два за-

кона. Согласно первому – закону смещения Вина

mT b1 , (27.11)

где b1 – постоянная Вина.

Первый закон смещения Вина объясняет, почему при нагревании тел они светятся сначала красным светом, переходя затем к белому калению

Согласно второму закону Вина максимум испускательной способности абсолютно черного тела возрастает пропорционально пятой степени абсолютной температуры.

. (27.12)

338

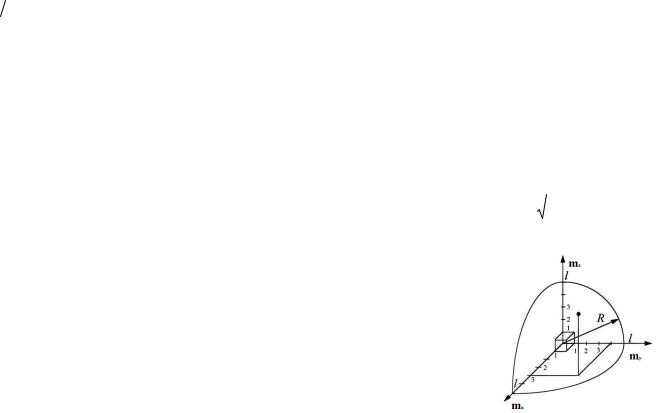
Формула Рэлея-Джинса. С точки зрения электромагнитной теории равновесное излучение в полости представляет собой систему стоячих волн с разными частотами , направлениями распространения и поляризациями. Найдем число различных стоячих волн в единице объема с частотами в интервале от до d . Допустим для простоты, что полость представляет собой куб с ребрами длины l, ориентированными вдоль координатных осей (результат, очевидно, не должен зависеть от формы полости).

Уравнение стоячей волны имеет вид

E A sin(kr ) , (27.13)

где E электрическое поле (аналогичное уравнение имеет место и для магнитного поля), k представляет собой волновой вектор, направление которого совпадает с направлением волны, а модуль равен k 2 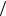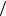c, – начальная фаза, и A – амплитуда

волны. Для поля должны выполняться периодические граничные условия. Физически это связано с тем, что в зависимости отражающих свойств стенок на них должны находиться либо узлы, либо пучности стоячих волн. Отсюда получаются условия

Введем пространство чисел mx , my , mz (рис. 27.5).

Рис. 27.5 Пространство чисел mx , my , mz

339

Каждой частоте соответствует в этом пространстве точка. На каждую точку приходится куб, с объемом равным единице. Число точек в сферическом слое с радиусом m и толщиной

dm равно с большой точностью объему этого слоя

Учитывая две независимые поляризации (на каждую точку приходится две волны), находим отсюда число стоячих волн

в интервале частот от до d

Согласно закону равнораспределения энергии по степеням свободы каждая колебательная степень свободы в состоянии равновесия имеет энергию kT. Половина из которой приходится на электрическую, другая на магнитную составляющую энергии волны. В результате получим

u ( ,T) kT 2 . (27.15)

2c3

Равенство (27.15) называется формулой Рэлея-Джинса. Она дает достаточно хорошее согласие с экспериментом при малых . При больших спектральная плотность значительно превосходит наблюдаемую. Полная объемная плотность излучения, согласно формулам (27.1) и (27.15), имеет бесконечно большое значение u(T) . Этот недопустимый результат (равновесная

величина u(T) имеет конечное значение) получил название

ультрафиолетовой катастрофы.

Формула Планка. С классической точки зрения вывод формулы Рэлея-Джинса является безупречным. В связи с этим возникла необходимость изменения некоторых положений классической теории.

В 1900 г. Планк предположил, что электромагнитное излучение испускается в виде отдельных порций, величина которых пропорциональна частоте излучения

Коэффициент пропорциональности получил впоследствии название постоянной Планка. Если излучение испускается порциями , то его энергия будет кратна этой величине

340

n n ,

где n – целое неотрицательное число.

В состоянии равновесия распределение энергии стоячей волны (моды колебаний) должно подчиняться распределению Больцмана. Вероятность того, что энергия моды колебаний имеет значение n , определяется выражением

Тогда средняя энергия данной моды найдется как

Pn n .

n

Проведя суммирование, получим

Заменив в (27.15) kT на полученное выражение , приходим к формуле Планка

Формула Планка точно согласуется с экспериментальными данными во всем интервале частот и дает исчерпывающее описание равновесного излучения. При условии kT 1 (малые частоты или большие длины волн) формула Планка переходит в формулу Рэлея-Джинса. С ее помощью можно также получить законы Стефана-Больцмана и Вина.

Оптическая пирометрия. Основываясь на законах теплового излучения, можно определять температуру раскаленных тел. Если испускающее тело является черным (или достаточно к нему приближается), то для определения его температуры можно воспользоваться законами черного излучения. По существу для сильно нагретых тел этот метод является единственным, другие методы не работают при таких температурах.

1. Радиационная температура. Это температура черно-

го тела Tp, при которой его энергетическая светимость равна