
Курс лекций Оптическая физика
.pdf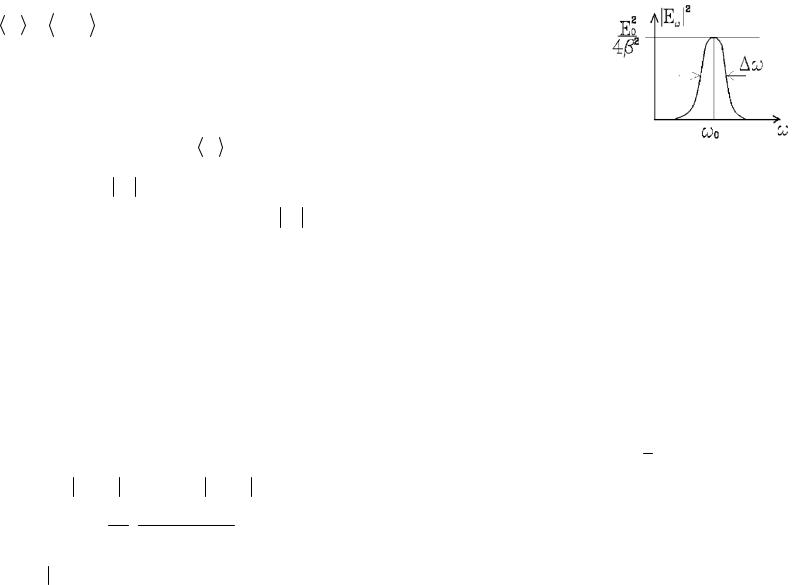
181
I |
t E2 (t) t |
E2 |
(t)dt E |
(E(t)exp( i t)dt) |
d |
; |
||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E(t)exp( i t)dt E . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Но так |
как |
функция |
|
|
E(t)вещественна, то |
||||||
|
|
|
|
|
|
|
|
2 |
d |
|
|
|
E* |
E* (t)e i tdt E , т.е. I |
|
|
E |
|
(15.7) |
||||||
|
|
|||||||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|||
Величина E 2 d - это доля энергии, уносимая волнами
с частотой от до d , т.е. величину E 2 можно назвать
спектральной плотностью энергии в немонохроматической волне (распределение энергии по частотам). Вычислим ее для
цуга волн
|
|
|
|
|
|
ei 0t |
|
e i 0t |
|
|
|
|
|
|||||
E E0e t ( |
|
|
)ei tdt |
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
E0 |
|
|
i( 0 ) |
|
|
i( 0 ) |
|
|
|||||||||
|
|
|
|
|
. |
|
||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|||||||||
2 |
|
|
( 0 ) |
|
|
2 |
( 0 ) |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
Так |
|
|
|
как |
|
|
|
|
|
|
затухание |
|
|
колебаний |
||||
1/ 108 с 1 света |
|
1015 с 1 , то функция |
E имеет два |
|||||||||||||||
острых пика вблизи 0 . Нас интересует положительная частота 0 в области
0 108 с 1 0 1015 с 1
т.е. E E20 2 i( 0 )2 .( 0 )
E |
|
|
2 |
|
E20 |
|
|
|
1 |
|
. (15.8) |
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
4 |
|
( 0 ) |
2 |
|||||
|
|
|
|
|
|
|
|
||||
182
Рис. 15.2. Лоренцев контур.
График этой функции называется лоренцевским конту-
ром спектральной линии.
Свет, испускаемый электронами, колеблющимися с частотой 0 , называется квазимонохроматическим - это набор
монохроматических волн с частотами очень близкими, а амплитудами, резко уменьшающимися по мере смещения частотыот частоты 0 .
Естественную частоту спектральной линии ха-
рактеризуют на уровне 50% от максимального значения графика
(полуширина резонансной кривой).
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
E2 |
|
|
|
E2 |
|
|
||||
( 0 )2 |
( |
|
)2 ; |
|
|
0 |
|
|
|
|
0 |
2 2 2 ( |
|
)2 |
|
|
|
2 |
|
|
2 |
|
2 4 2 |
2 |
|||||||
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
4( |
|
( |
|
) |
|
) |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и 2 1.
Полуширина спектральной линии обратно пропорциональна времени релаксации . Чем больше радиационное затухание (потеря энергии атомами) тем шире и ниже спектральная линия (удаление от монохроматичности света).
Но такой характер излучения был получен для одного атома. А что будет для суммарного излучения множества N атомов, которые начинают излучать случайным образом в раз-
N
ные моменты времени tk : Eрез (t) E(t tk ).
k 1

183
Подставляя разложение в интеграл Фурье, получим
|
i t d |
N |
|
|
i (t tk ) d |
||
Eрез (t) Eрез e |
|
|
E |
e |
|
|
|
|
2 |
|
2 |
||||
|
|
k 1 |
|
|
|
||
N |
|
|
|
|
|
|
|
Тогда Eрез E ei tk .
k 1
Результирующая спектральная плотность излучаемой энергии усредняется по всем моментам времени:
|
|
|
|
2 |
|
N |
|
|
|
|
|
|||
Eрез |
|
|
E ei tk )E* e i t j ) |
|
||||||||||
|
|
|
|
|
|
|
k,j 1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
N |
|
|
|
|
|
||
N |
|
E |
|
2 |
|
|
E |
|
2 2 |
cos (tk |
tj . |
|||
|
|
|
|
|||||||||||
k,j 1
Второе слагаемое равно нулю, так как моменты излучения отдельных атомов совершенно случайны.
Энергии или интенсивности, излучаемые каждым от-
дельным атомом, просто складываются: Eрез 2 NE 2 .
Рис. 15.3. Схема излучения атома.
Спектральная линия, т.е. распределение излучаемых ча-
стот для многих атомов, такая же, как для отдельного атома.
При этом неважно, накладываются отдельные цуги один на другой или испускаются один за другим, главное, чтобы N>>1.
Каждый отдельный атом испускает поляризованный свет. При произвольном угле наблюдается эллиптическая поляризация. При = 90° - линейная поляризация. При =0° - круговая поляризация. Эта поляризация сохраняется на время длительности цуга 10 8 с.
184
Если бы приборы измеряли свет мгновенно, то в каждый момент они показывали бы какую-то поляризацию. Но для них
время срабатывания 10 2 с (болометры).
В разных атомах электроны вращаются в разных плоскостях и последующие цуги, испускаемые другими атомами, имеют другую поляризацию. В сумме по лучается естественный (неполяризованный) свет.
Изменение спектральных характеристик света при учете взаимодействия атомов. Уширение спектральных линий
До сих пор рассматривали излучение невзаимодействующих покоящихся (или движущихся с одинаковой скоростью к наблюдателю) атомов.
Рассмотрим излучение газов (газонаполненные лампы, ртутные лампы и т.д.).
Если плотность газа большая (р ~ 1атм), то атомы сталкиваются друг с другом случайным образом. Среднее
|
|
19 |
|
|
|
|
1 |
|
время между соударениями атомов уд |
10 |
|
с |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
. |
||||
|
|
|
|
|
|
столкн |
||
Рис. 15.4. Гармоническое приближение цуга.
Но при соударениях излучение атомов прекращается, поэтому испущенный цуг имеет вид практически отрезка монохроматической волны:
|
|
E(t) E0 cos 0t |
при |
уд |
t |
уд |
,E(t) 0 при |
|
2 |
||||||
|
уд |
|
2 |
|
|
||
t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
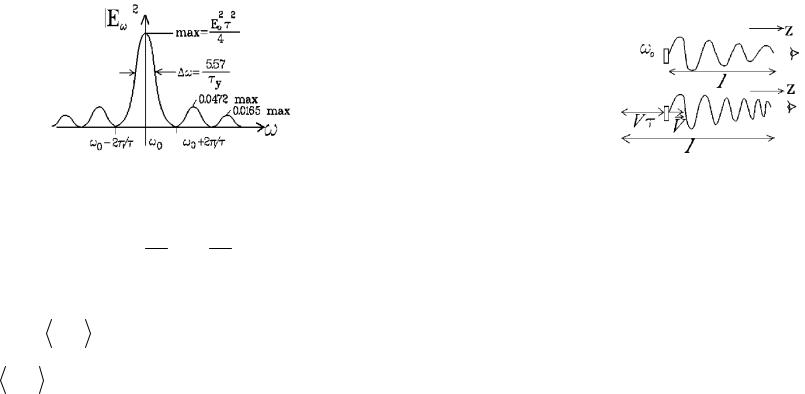
185
Для простоты выкладок время начала цуга смещено. Длина цуга c уд 30см.
|
|
|
|
|
|
|
|
|
|
/ 2 |
|
d |
|
|
Разлагая |
в |
интеграл ФурьеE |
E0e i t cos 0t |
, |
||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
/ 2 |
|
2 |
||
получим функцию, имеющую острый |
пик вблизи |
частоты |
||||||||||||
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
sin2 ( 0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
E |
|
2 |
E |
2 |
2 |
|
|
(15.9). |
|
|
|
||
|
|
|
|
|
||||||||||
|
|
|
0 |
( 0 )2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
Эта спектральная линия получалась бы, если бы все атомы излучали отрезки волн одинаковой длины.
Рис. 15.5. Спектр гармонического цуга.
На самом деле столкновения атомов - это случайные процессы. Некоторые столкнутся раньше, другие позже. Случайные события распре делены в соответствии с распределени-
ем Гаусса: P(t)dt 1 exp( t )dt- это вероятность того,
уд уд
что цуг имеет длительность от t до t + dt. Тогда средняя (результирующая) спектральная плотность энергии, испущенная одним
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 P(t)dt . |
Вводя уд 1/ уд , получаем |
|||
атомом |
|
E |
|
|
|
E |
|
||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
E |
|
|
2 |
|
|
|
|
E02 |
|
|
|
- такой же лоренцевский контур, но |
||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2( 0 )2 |
2уд |
|||||||||||||
|
|
|
|
|
|||||||||||||
|
186 |
значительно более широкий, т.к. уд |
109 с 1 , а не |
рад.зат. 10 8 с. Уширение линии при частых столкновениях атомов велико 1/ уд 109 с 1 . Оно на порядок больше
естественной ширины спектраль ной линии.
Другой причиной уширения линии (особенно в газоразрядной плазме низ кого давления, в лазерах, где столкно-
вения атомов друг с другом очень редки, уд 10 8 с) будет
эффект Доплера.
Если источник света неподвижен, находится первоначально на удалении от фотоприемника и испускает цуг из n максимумов за время , то конец цуга придет к фотоприемнику через время после начала и частота колебаний 0 2 n / .
Рис. 15.6. Иллюстрация эффекта Доплера.
Но если источник движется со скоростью V (к приемнику), то начало цуга придет через время /c, а конец - через вре-
мя |
( V )/c (источник сместится |
наV ), т.е. длитель- |
ность цуга для глаза будет (1 V/c) , |
а частота колебаний |
|
0 |
2 n / (1 V/c). Цуг как бы сжимается V>0 или растяги- |
|
вается V<0.
Но атомы газа движутся с разными скоростями вдоль выделенного направления Z. В соответствии с распределением Максвелла вероятность того, что скорости лежат в интервале от V до V+dV будет
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
187 |
|
|
|
|
|
|
|
|
|
|
|
mV2 |
|
|
|
|
|
||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|||||
f(V)dV |
|
|
|
exp( |
|
|
|
|
)dV. |
|
|
|
||||||||
2 kT |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
|
|
||||||
Делаем |
замену |
|
|
V |
( 0 )c |
и |
получаем |
|||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
||||
|
m |
|
|
c |
|
|
|
mc |
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
P( )d |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
exp |
|
|
|
0 |
|
|
d |
|
|||||||||||
|
2 kT 0 |
|
|
|
|
2kT |
|
|
|
|
|
|||||||||
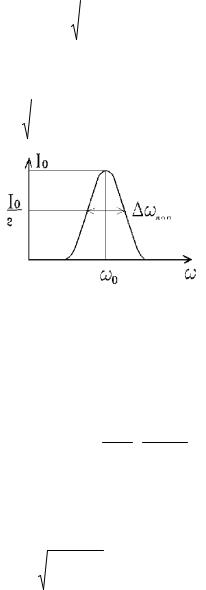
Рис. 15.7. Распределение по частотам.
Получили вероятность того, что частоты лежат в интервале от до d . Это частоты излучения самих атомов 0 и
каждая из них "уширяется" при излучении в естественную ширину спектральной линии. Интенсивность излучения пропорциональна числу излучающих атомов в каждом интервале, т.е. гауссова кривая интенсивности излучения движущихся атомов
I I0 exp mc2 0 2 .2kT 0
Полуширину доплеровской линии находим из условия
I0 |
|
|
|
mc |
2 |
|
|
доп |
2 |
|
|
I0 |
exp |
|
|
|
|
|
|
или |
|||
|
|
|
|
|
|||||||
2 |
|
|
|
2kT |
|
2 0 |
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
2 |
2kTln2 |
. |
|
|
|||
|
доп |
0 |
mc2 |
|
188
Так для зеленой линии натрия при температуре 300К по-
лучим доп 8,66 109 с 1 . Это на два порядка больше есте-
ственной ширины спектральной линии.
Ширина спектральной линии, излучаемой возбужденными атома ми, возрастает на два порядка из-за движения атомов, приводящего к доплеровскому смещению частот, и возрастает на порядок в "плотных" газах из-за частого столкновения атомов друг с другом.
Вопросы:
1.Основа Фурье анализа?
2.Как связаны колебания атомов и линии спектра?
3.Принцип неопределенности в спектральном анализе?
4.Чем определяется ширина спектральной линии?
5.Какие факторы влияют на ширину спектральной линии?
6.Какова ширина спектральной линии безкочечного гармонического колебания?
189
8. Интерференция световых волн
Лекция 16
Условия интерференции электромагнитных волн Когерентность волн и когерентные источники света
Как создать когерентные источники Когерентность лазерного излучения Интерференция поляризованного света Оптическая схема Юнга
Условия интерференции электромагнитных волн. Когерентность волн и когерентные источники света
Пусть свет от двух удаленных источников падает в некоторую точку Р экрана (точка
Рис. 16.1. Схема сложения волн.
наблюдения). На большом удалении (в волновой зоне) эти волны можно считать плоскими. Сложим их методом векторной
диаграммы:
Ep E1 cos( 1t k1r 1) E2 cos( 2t k2 r 2 )
1). Так можно складывать однонаправленные коле-
бания, т.е. считаем, что волны приходят к экрану под очень малым углом 1 (источники очень удалены) и практи-
чески E1 E1x , E2 E2x
190
Рис. 16.2. Графическое сложение амплитуд.
2). Частоты источников должны быть одинаковыми:1 2 , иначе результирующий вектор будет очень быстро изменяться со временем. Тогда
E2p E12 E22 2E1E2 cos( 2 1)
Усредняя по времени, находим результирующую интенсивность света (световой поток, освещенность экрана, и т.п., все
они пропорциональны 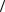 E2
E2 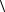 ):
):
Ip I1 I2 2
 I1I2 cos( 2 1),I const
I1I2 cos( 2 1),I const  E2
E2  .
.
Волны, у которых разность фаз зависит от времени, называются некогерентными, для них  cos( 2 1)
cos( 2 1) 0.
0.
При сложении некогерентных световых волн их интенсивности просто складываются и одинаковы во всех точках пространства.
Волны, у которых разность фаз не зависит от времени,
называются когерентными: |
2 1 |
f(r) const |
в каждой |
|
точке |
пространства. |
Для |
когерентных |
волн |
Ip I1 I2 2
 I1I2 cos( 2 1).
I1I2 cos( 2 1).
В тех точках пространства, где разность фаз двух складывающихся когерентных волн равна четному числу , получим усиление интенсивности:
Ipmax (
 I1
I1 
 I2 )2
I2 )2
а в тех точках, где она равна нечетному числу к, получим ослабление интенсивности:
191
Ipmin (
 I1
I1 
 I2 )2 (9.1)
I2 )2 (9.1)
Это явление называют интерференцией.
Интерференционная картина - это устойчивая во времени картина чередующихся максимумов и минимумов освещенности на экране. Получается она только при сложе-
нии когерентных волн. Если в данной точке экрана разность фаз волн 2 1 2 m, m 0, 1, 2,... - это условие интерференционного максимума,
Если 2 1 (2m 1) , m 0, 1, 2,... - целое - это условие интерференционного минимума.
Условие интерференционных максимумов можно переписать по-другому:
( t k1s1 1) ( t k2s2 2 )
2 |
. |
|
(n2s2 n1s1) ( 1 2 ) |
||
0 |
||
|
Сдесь: λ0-длина волны в вакууме, n-показатель преломления среды, s-путь пройденный в среде. Назовем ns-
оптическим путем, тогда n2s2-n1s1=Δ-оптическая разность хода лучей. Пусть для простоты когерентные источники колеблются с одной начальной фазой. Тогда получим
2m m - интерференционный максимум;
2
(2m 1) - интерференционный минимум.
2
Величина n(s2 s1 )называется оптической разностью хода лучей (это геометрическая разность пути, умноженная на показатель преломления среды).
Как создать когерентные источники
Если источник света протяженный, то разные участки его испускают цуги волн с совершенно случайными фазами2 1 f(t) (свет испускается случайно разными атомами).
Поэтому разные участки светящегося тела или разные светящиеся тела не могут быть когерентными. Исключение - излучение лазеров.
192
Для создания двух или более когерентных лучей надо использовать один источник и разделить его на два или более луча, т.е. надо создать изображения источников. Но покоящиеся атомы испускают короткие цуги с 3м и, если s2 s1
, то в точку наблюдения придут цуги, испущенные разными атомами, т.е. лучи перестанут быть когерентными. Это сильно ограничивает размер интерференционной картины.
Но значительно сильнее ограничивает этот размер немонохроматичность света и конечный размер источников света.
Рис. 16.3. Разбиение излучения атома на составляющие и их сложение.
Каждый атом S создаст изображения в S1 и S2, которые когерентны и создадут в точке Р интерференционную картину. Но такие же картины создадут и все остальные атомы.
Из рис. 16.3 видно, что n(s2 s1 ) n(s2 s1 ) т.е. в точке Р накладываются интерференционные максимумы, созданные одними участками светящегося тела с минимумами от других участков. В сумме получается равномерно освещенная поверхность (без интерференционных полос).
Но даже если источники очень малы - их атомы испус-
кают естественную спектральную линию 108 1010 с-1- смесь монохроматических волн с разными длинами. Следовательно, максимумы для одних длин волн накладываются на минимумы для других, и интерференционная картина исчезает.
Вывод: создать интерференционную картину для обычных источников света очень сложно.
Когерентность лазерного излучения
Чтобы заставить атомы излучать электромагнитную волну их надо возбудить, т.е. перевести электроны на более уда-
193
ленную боровскую орбиту. Возвращаясь в основное состояние в течение 10 8 с электрон испускает цуг длительностью
10 8 с. Это - естественное (спонтанное) излучение.
Но оно нарушает термодинамическое равновесие: возбуждать атомы можно практически мгновенно ("обстреливая " их, например, потоком фотонов), а возвращаются они в основное состояние через ~ 10-8 с, т.е. атомы будут накапливать энергию, а температура газа - расти.
Эйнштейн показал, что такого нарушения термодинамического равновесия не происходит из-за появления вынужденного излучения.
Если на возбужденный атом попадает фотон с энергией, равной разности энергий электрона в основном и возбужденном состоянии, то этот электрон практически мгновенно переходит в основное состояние, а испущенный им фотон имеет ту же частоту, ту же начальную фазу и то же направление движения, что и налетающий фотон.
Такие фотоны вынужденного излучения образуют плоскую волну — луч вынужденного излучения, выходящий из лазера очень слабо расширяется в пространстве, в отличие от естественного (спонтанного) излучения.
Рис. 16.4. Получение интерференции с помощью лазера.
За время с 10 9 10 8 свсе возбужденные атомы
возвращаются в основное состояние, и из выходного отверстия вылетает практически монохроматическая (бесконечная) плоская волна. Все ее участки когерентны и при наложении дают интерференционную картину произвольного размера и на произвольном удалении.
Интерференция поляризованного света.
194
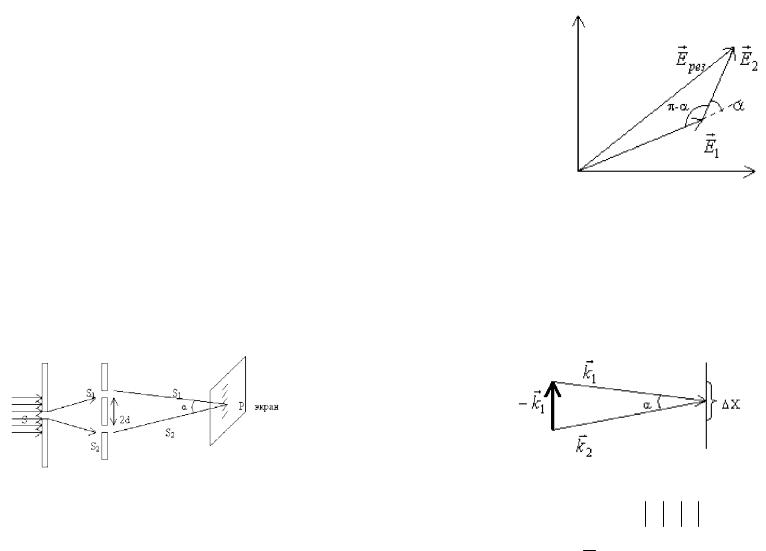
Интерференционную картину создают только те когерентные волны, в которых колебания векторов Е однонаправленны. Так, если в точку Р плоскополяризованные в плоскости падения лучи от когерентных источников S1 и S2 придут под большим углом, то интерферировать будут только составляющие Е1x и Е2x.
Рис. 16.5. Сложение различных составляющих. Перпендикулярные к экрану составляющие E1z и E2z со-
здают равномерное освещение, как и некогерентные волны. Такой свет частично когерентен. Освещенность в точке Р будет равна
Ip I1x I2x 2
 I1xI2x cos( 2 1) I2z I1z I2y I1y
I1xI2x cos( 2 1) I2z I1z I2y I1y
Эти полосы интерференции видны хуже. Они наблюдаются на фоне равномерно освещенного экрана. Для описания подобной интерференционной картины вводят функцию видности:
V |
Imax Imin |
|
(16.2) |
|
|
|
|
|
||||||
Imax Imin |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||
Для рассматриваемого на рисунке случая |
||||||||||||||
( |
|
|
|
|
)2 ( |
|
|
|
)2 |
|
||||
I1x |
I |
2x |
I1x |
I2x |
||||||||||
V |
|
|
|
|
|
|
|
- когда эта вели- |
||||||
2(I1x I2x |
|
|
|
|
|
|
||||||||
|
I1y I2y I1z I2z ) |
|||||||||||||
чина видности < 50 %, то полосы трудно увидеть.
Обычно наблюдают интерференцию в естественном свете, где параллельные и перпендикулярные составляющие дают
195
две независимые интерференционные картины. Но, так как скорости || и лучей одинакова, то и проходимые ими оптические пути одинаковы. Поэтому картины совпадают друг с другом (их максимумы и минимумы подчиняются одному условию).
В опытах Френеля и Араго на пути лучей ставились поляризаторы. Когда угол между плоскостями пропускания поляризаторов был равен 90°, они пропускали взаимно перпендикулярно поляризованный свет, и интерференционная картина на экране исчезала.
Если на пути одного из лучей поставить оптически активное вещество, которое вращает плоскость поляризации на 90°, то интерференционная картина также исчезнет, так как теперь складываются однонаправленные колебания
E1|| иE1 ,E1 и E1|| , а они испущены разными атомами и некогерентны.
Оптическая схема Юнга
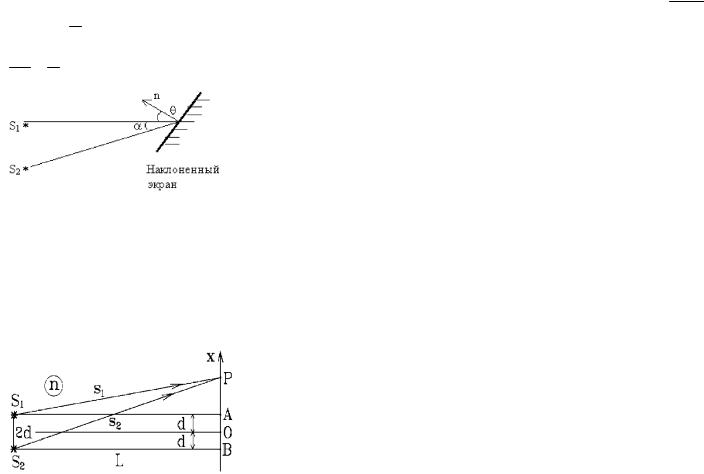
Оптическая схема Юнга - это случай интерференции, когда расстояние 2d между когерентными источниками много меньше расстояния L до экрана.
Томас Юнг в 1802 г. впервые наблюдал интерференционную картину. В узкие отверстия S1 и S2 попадает свет от одного источника S , т.е. S1 и S2 будут когерентными источниками.
Рис. 16.6 Схема Юнга.
Крохотный размер S, S1, S2 обеспечивает видимость интерференционной картины, но резко уменьшает освещенность экрана.
Для усиления освещенности используют узкие прорезищели. Световые волны от разных точек щели складываются на
196
экране, и образуется интерференционная картина из параллельных полос.
Рис. 16.7. Сложение напряженностей от двух щелей. Определим ширину полос, полученных при сложении
двух плоских когерентных волн, сходящихся на экране под малым углом . Так как
E |
рез |
E |
1 |
cos( t k |
1 |
r |
) E |
cos( t k |
2 |
r |
2 |
), |
|
|
|
|
1 |
|
2 |
|
|
|
|||||
Eрез2 |
E12 |
E22 2E1E2 cos((k2 |
k |
1)r ( 2 |
1)) |
|
|||||||
то линией с одинаковой освещенностью на экране будет линия
(k2 k1)r const.
Рис. 16.8. Условие одинаковой освещенности.
Пусть экран перпендикулярен падающему свету или
(k2 k1)x const,(k2 k1 k)
или 2ksin x const 2
197
Расстояние между соседними интерференционными максимумами (или минимумами), т.е. ширина интерференционной полосы из условия
2sin x 2 , при 1рад, имеет величи-
2
ну x 2 .k
Рис. 16.9. Учет наклона экрана.
Чем меньше угол схождения плоских волн, тем большеx . Если экран наклонить под углом θ, то ширина интерферен-
ционных полос на нем увеличится: x |
|
|
|
(16.3). |
|
|
||
cos
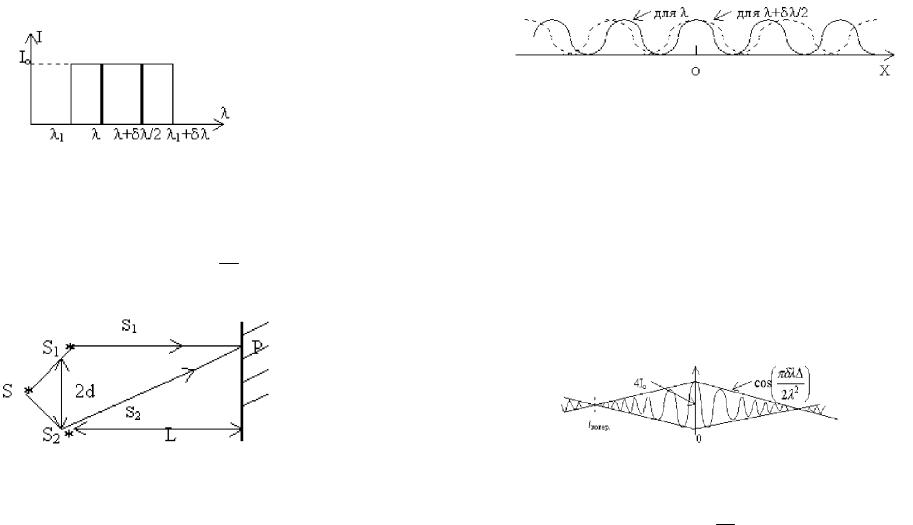
Получим далее выражение для освещенности интерференционной картины в опыте Юнга более детально.
Из S2BP и S1AP получим
Рис. 16.10. Расчет освещенности интерференционной картины в опыте Юнга.
S22 L2 (x d)2 ,
S12 L2 (x d)2
198
S22 S12 (S2 S1)(S2 S1) 4xd,
n(S2 S1) 2xdn L
Если оптическая разность хода равна четному числу полуволн, то на экране видны светлые полосы с максимумами в
точках с |
координатами xmax |
|
L |
m m - |
|
целое. Минимумы |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2nd |
|
|
|
|
|
|
|
|
|
|
|
|
|
освещенности наблюдаются между ними в точках с координа- |
|
|
|
|
|||||||||||||||||||||
тами xmin |
|
L (2m 1) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
4nd |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Расстояние между соседними полосами, или ширина ин- |
|
|
|
|
|||||||||||||||||||||
терференционной |
|
|
|
полосы |
на |
экране, |
|
|
|
|
|||||||||||||||
x xm 1 |
xm |
L |
|
(тт.к |
2d |
tg ,тт x |
|
). |
|
|
|
|
|
|
|
||||||||||
2nd |
L |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||
Квадрат результирующей амплитуды светового вектора |
|
|
|
|
|||||||||||||||||||||
на экране |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2xd |
|
|
|
|
|
|
E2 |
|
E2 |
E2 |
2E E |
2 |
cos(k ) 2E |
0 |
(1 cos( |
n |
)),E |
1 |
E |
2 |
|
|||||||||||
|
|
|
|||||||||||||||||||||||
рез |
1 |
2 |
1 |
|
|
|
|
|
|
|
|
L |
|
|
|||||||||||
, или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 nxd |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Iрез |
4I0 cos2( |
) |
|
(16.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда
199
Лекция 17
Условия временной когерентности Видность интерференционных полос Длина когерентности излучения
Условия временной когерентности.
Рис. 17.1. Спектр складываемых колебаний.
Выясним как влияет на интерференционную картину немонохроматичность источника, испускающего волны с длиной от 1 до 1 . Пусть для простоты интенсивность этих волн одинакова и равна I0. Разобьем сплошной спектр из луче-
ния на попарные компоненты и . Обе проходят до
2
точки наблюдения Р на экране одинаковые пути S2 и S1. Первая дает освещенность экрана
Рис. 17.2. Схема сложения колебаний.
|
/ |
|
|
2 |
|
|
I |
|
2I |
0 1 cos |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
для второй
200
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
I |
// |
|
|
|
|
|||
|
|
|
|
|
||||
|
2I0 1 cos |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 17.3. Сложение колебаний с разной длиной волны. Из-за того, что λ разное ( одинаково) для них не совпа-
дают координаты интерференционных максимумов Максимумы одной длины волны накладываются на ми-
нимумы другой, и интерференционная картина вдали от центра экрана исчезает
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
Iрез 2I0 |
2 cos |
|
|
|
|
|
|
|
|
|||||
|
cos |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(17.1) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4I |
0 1 cos |
|
cos |
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
т.е. картина, видимая на экране имеет вид:
Рис. 17.4. Вид интерференционной картины при сложении немонохроматических колебаний.
Тот же самый результат получится для любой другой
пары компонент, сдвинутых на .
2
