Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный индустриальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

basic mathematics for college students.pdf

Скачиваний:

147

Добавлен:

10.06.2015

Размер:

15.55 Mб

Скачать

☆

<<< < Предыдущая 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 5960 / 6760 61 62 63 64 65 66 67 > Следующая >>>

S E C T I O N 9.4

The Pythagorean Theorem

A theorem is a mathematical statement that can be proven. In this section, we will discuss one of the most widely used theorems of geometry—the Pythagorean theorem. It is named after Pythagoras, a Greek mathematician who lived about 2,500 years ago. He is thought to have been the ﬁrst to develop a proof of it. The Pythagorean theorem expresses the relationship between the lengths of the sides of any right triangle.

9.4 The Pythagorean Theorem

747

Objectives

1Use the Pythagorean theorem to ﬁnd the exact length of a side of a right triangle.

2Use the Pythagorean theorem to approximate the length of a side of a right triangle.

3Use the converse of the Pythagorean theorem.

1Use the Pythagorean theorem to ﬁnd the exact length of a side of a right triangle.

Recall that a right triangle is a triangle that has a		Hypotenuse
right angle (an angle with measure 90°). In a right	Leg
triangle, the longest side is called the hypotenuse. It		c
triangle, the longest side is called the hypotenuse. It	a
is the side opposite the right angle. The other two
sides are called legs. It is common practice to let the		b
variable c represent the length of the hypotenuse		Leg
and the variables a and b represent the lengths of the

legs, as shown on the right.
If we know the lengths of any two sides of a right triangle, we can ﬁnd the length
of the third side using the Pythagorean theorem.	Pythagoras

Pythagorean Theorem

If a and b are the lengths of two legs of a right triangle and c is the length of the hypotenuse, then

a2 b2 c2

In words, the Pythagorean theorem is expressed as follows:

In a right triangle, the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse.

Caution! When using the Pythagorean equation a2 b2 c2, we can let a represent the length of either leg of the right triangle. We then let b represent the length of the other leg. The variable c must always represent the length of the hypotenuse.

	EXAMPLE 1	Find the length of the hypotenuse of

the right triangle shown here.			3 in.
Strategy We will use the Pythagorean theorem to ﬁnd the			4 in.
length of the hypotenuse.

WHY If we know the lengths of any two sides of a right triangle, we can ﬁnd the length of the third side using the Pythagorean theorem.

Self Check 1

Find the length of the hypotenuse of the right triangle shown below.

5 ft

12 ft

EXAMPLE 2

748	Chapter 9 An Introduction to Geometry

Now Try Problem 15

Self Check 2

In Example 2, can the crews communicate by radio if the distance from point B to point C remains the same but the distance from point A to point C increases to 2,520 yards?

Now Try Problems 19 and 43

Solution We will let a 3 and b 4,and substitute into the Pythagorean equation to ﬁnd c.

a2 b2				c2		This is the Pythagorean equation.	a = 3 in.	c
3	2	4	2	c	2	Substitute 3 for a and 4 for b.

9 16				c2		Evaluate each exponential expression.		b = 4 in.
		25		c2		Do the addition.

		c2		25		Reverse the sides of the equation so that c2 is on the left.

To ﬁnd c, we must ﬁnd a number that, when squared, is 25. There are two such numbers, one positive and one negative; they are the square roots of 25. Since c


represents the length of a side of a triangle, c cannot be negative. For this reason,
we need only ﬁnd the positive square root of 25 to get c.
c 1		The symbol 2			is used to indicate the positive square root of a number.
	25
c 5		1		5 because 52 25.
			25

The length of the hypotenuse is 5 in.

Success Tip The Pythagorean theorem is used to ﬁnd1 the lengths of sides of right triangles. A calculator with a square root key is often helpful in the ﬁnal step of the solution process when we must ﬁnd the positive square root of a number.

Fireﬁghting To ﬁght a forest ﬁre, the forestry department plans to clear a rectangular ﬁre break around the ﬁre, as shown in the following ﬁgure. Crews are equipped with mobile communications that have a 3,000-yard range. Can crews at points A and B remain in radio contact?

Strategy We will use the Pythagorean theorem to ﬁnd the distance between points A and B.

WHY If the distance is less than 3,000 yards, the crews can communicate by radio. If it is greater than 3,000 yards, they cannot.

Solution The line segments connecting		A

points A, B, and C form a right triangle.		1,000 yd	c
To ﬁnd the distance c from point A to

point B, we can use the Pythagorean
equation, substituting 2,400 for	a and	C	2,400 yd	B
1,000 for b and solving for c.


a2 b2 c2	This is the Pythagorean equation.
2,4002 1,0002 c2	Substitute for a and b.
5,760,000 1,000,000 c2	Evaluate each exponential expression.
6,760,000 c2	Do the addition.
c2 6,760,000		Reverse the sides of the equation so that
c 16,760,000		c2 is on the left.
		If c2 6,760,000, then c must be a
		square root of 6,760,000. Because c
		represents a length, it must be the positive
		square root of 6,760,000.
c 2,600		Use a calculator to ﬁnd the square root.

The two crews are 2,600 yards apart. Because this distance is less than the 3,000yard range of the radios, they can communicate by radio.

EXAMPLE 3

The lengths of two sides of a right triangle are given in the ﬁgure. Find the missing side length.

Strategy We will use the Pythagorean theorem to ﬁnd the missing side length.

WHY If we know the lengths of any two sides of a right triangle, we can ﬁnd the length of the third side using the Pythagorean theorem.

Solution We may substitute 11 for either a or b, but 61 must be substituted for the length c of the hypotenuse. If we choose to substitute 11 for b, we can ﬁnd the unknown side length a as follows.

61ft

11 ft

c = 61 ft

a2 b2	c2
a2 112	612
a2 121	3,721
a2 121 121	3,721 121
a2	3,600
a	1
		3,600

This is the Pythagorean equation.

Substitute 11 for b and 61 for c.	b = 11 ft
Substitute 11 for b and 61 for c.
Evaluate each exponential expression.
To isolate a2 on the left side, subtract		3,721
To isolate a2 on the left side, subtract		3,721
121 from both sides.		121
Do the subtraction.		3,600
Do the subtraction.

If a2 3,600, then a must be a square root of 3,600.

Because a represents a length, it must be the positive square root of 3,600.

a 60	Use a calculator, if necessary, to ﬁnd the square root.

The missing side length is 60 ft.

9.4 The Pythagorean Theorem

749

Self Check 3

The lengths of two sides of a right triangle are given. Find the missing side length.

65 in.

33 in.

Now Try Problem 23

2Use the Pythagorean theorem to approximate the length of a side of a right triangle.

When we use the Pythagorean theorem to ﬁnd the length of a side of a right triangle, the solution is sometimes the square root of a number that is not a perfect square. In that case, we can use a calculator to approximate the square root.

	EXAMPLE 4	Refer to the right triangle shown		2 in.

here. Find the missing side length. Give the exact answer
			6 in.

and an approximation to the nearest hundredth.

Strategy We will use the Pythagorean theorem to ﬁnd the missing side length.

WHY If we know the lengths of any two sides of a right triangle, we can ﬁnd the length of the third side using the Pythagorean theorem.


Solution We may substitute 2 for either a or b, but 6
Solution We may substitute 2 for either a or b, but 6			b
must be substituted for the length c of the hypotenuse.				a = 2 in.


If we choose to substitute 2 for a, we can ﬁnd the
If we choose to substitute 2 for a, we can ﬁnd the			c = 6 in.
unknown side length b as follows.			c = 6 in.
unknown side length b as follows.
a2 b2	c2	This is the Pythagorean equation.
22 b2	62	Substitute 2 for a and 6 for c.
4 b2	36	Evaluate each exponential expression.
4 b2 4 36 4 To isolate b2 on the left side, undo the addition of 4 by
		subtracting 4 from both sides.
b2	32	Do the subtraction.

Self Check 4

Refer to the triangle below. Find the missing side length. Give the exact answer and an approximation to the nearest hundredth.

5 m

7 m

Now Try Problem 35

750 Chapter 9 An Introduction to Geometry

We must 1ﬁnd a number that, when squared, is 32. Since b represents the length of a side of a triangle, we consider only1the positive square root.

b 32 This is the exact length. 1

The missing1 side length is exactly 32 inches long. Since 32 is not a perfect square, its square root is not a whole number. We can use a calculator to approximate 32. To the nearest hundredth, the missing side length is 5.66 inches.

32 in. 5.66 in.

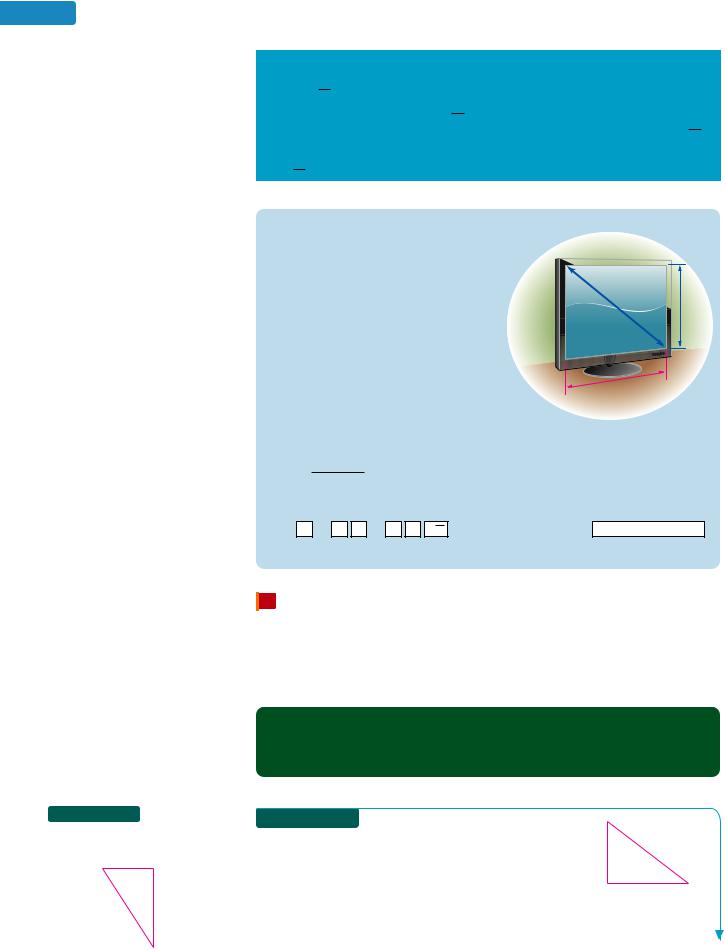
Using Your CALCULATOR Finding the Width of a TV Screen

The size of a television screen is the diagonal measure of its rectangular screen. To ﬁnd the length of a 27-inch screen that is 17 inches high, we use the Pythagorean theorem

with c 27 and b 17.

c2 a2 b2

272 a2 172

272 172 a2

27 in.	17 in.

a in.

Since the variable a represents the length of

the television screen, it must be positive. To ﬁnd a,

we ﬁnd the positive square root of the result when 172 is subtracted from 272.
Using a radical symbol to indicate this, we have
2272 172 a
We can evaluate the expression on the left side by entering:
( 27 x2 17 x2 )	1	20.97617696

To the nearest inch, the length of the television screen is 21 inches.

3 Use the converse of the Pythagorean theorem.

If a mathematical statement is written in the form if p . . . , then q . . . , we call the statement if q . . . , then p . . . its converse. The converses of some statements are true, while the converses of other statements are false. It is interesting to note that the converse of the Pythagorean theorem is true.

Converse of the Pythagorean Theorem

If a triangle has three sides of lengths a, b, and c, such that a2 b2 c2, then the triangle is a right triangle.

Self Check 5

Is the triangle below a right triangle?

	48 ft
73 ft	55 ft
73 ft

	EXAMPLE 5	Is the triangle shown here a right
triangle?		11 m

6 m

Strategy We will substitute the side lengths, 6, 8, and

11, into the Pythagorean equation a2 b2 c2.

8 m

WHY By the converse of the Pythagorean theorem, the

triangle is a right triangle if a true statement results. The triangle is not a right triangle if a false statement results.

9.4	The Pythagorean Theorem	751
Solution We must substitute the longest side length, 11, for c, because it is the	Now Try Problem 39
possible hypotenuse. The lengths of 6 and 8 may be substituted for either a or b.

a2 b2	c2	This is the Pythagorean equation.
62 82	112	Substitute 6 for a, 8 for b, and 11 for c.
36 64	121	Evaluate each exponential expression.
100	121	This is a false statement.

Since 100 121, the triangle is not a right triangle.

ANSWERS TO SELF CHECKS	124 m 4.90 m 5. yes
1. 13 ft 2. no 3. 56 in. 4.

3664 100

S E C T I O N 9.4 STUDY SET

VOCABULARY

Fill in the blanks.

1. In a right triangle, the side opposite the 90° angle is called the . The other two sides are called


2.	The Pythagorean theorem is named after the Greek
	mathematician,		, who is thought to have
	been the ﬁrst to prove it.
3.	The	theorem states that in any right
	triangle, the square of the length of the hypotenuse is
	equal to the sum of the squares of the lengths of the
	two legs.
4.	a2 b2 c2 is called the Pythagorean			.

CONCEPTS

Fill in the blanks.

5.If a and b are the lengths of two legs of a right triangle and c is the length of the hypotenuse, then .

6.The two solutions of c2 36 are c or c . If c represents the length of the hypotenuse of a right triangle, then we can discard the solution .

7.The converse of the Pythagorean theorem: If a

triangle has three sides of lengths a, b, and c, such that a2 b2 c2, then the triangle is a

triangle.

8.Use a protractor to draw an example of a right triangle.

9. Refer to the triangle on the right.	C

a.	What side is the hypotenuse?		60°
	What side is the longer leg?		60°
b.	What side is the longer leg?
c.	What side is the shorter		30°
	leg?	B		A
		B		A

10.What is the ﬁrst step when solving the equation 25 b2 81 for b?

NOTATION

Complete the solution to solve the equation, where a 0 and c 0.

11.82 62 c2

1 36 c2

10 c

12.a2 152 172

a2
a2 225	a 1
a2 225		289

752	Chapter 9 An Introduction to Geometry

GUIDED PRACTICE

Find the length of the hypotenuse of the right triangle shown below if it has the given side lengths. See Examples 1 and 2.

13.	a 6 ft and b 8 ft
14.	a 12 mm and b 9 mm	a

15.a 5 m and b 12 m

16.a 16 in. and b 12 in.

17.a 48 mi and b 55 mi

18.a 80 ft and b 39 ft

19.a 88 cm and b 105 cm

20.a 132 mm and b 85 mm

Refer to the right triangle below. See Example 3.

21.Find b if a 10 cm and c 26 cm.

22.Find b if a 14 in. and c 50 in.

23.Find a if b 18 m and c 82 m.

24.Find a if b 9 yd and c 41 yd.

25.Find a if b 21 m and c 29 m.

26.Find a if b 16 yd and c 34 yd.

27.Find b if a 180 m and c 181 m.

28.Find b if a 630 ft and c 650 ft.

The lengths of two sides of a right triangle are given. Find the missing side length. Give the exact answer and an approximation to the nearest hundredth. See Example 4.

29.	a 5 cm and c 6 cm
	a	c
	a
30.	a 4 in. and c 8 in.

31.a 12 m and b 8 m

32.a 10 ft and b 4 ft

33.a 9 in. and b 3 in.

34.a 5 mi and b 7 mi

35.b 4 in. and c 6 in.

36.b 9 mm and c 12 mm

Is a triangle with the following side lengths a right triangle?

See Example 5.

37.12, 14, 15

38.15, 16, 22

39.33, 56, 65

40.20, 21, 29

APPLICATIONS

41.ADJUSTING LADDERS A 20-foot ladder reaches a window 16 feet above the ground. How far from the wall is the base of the ladder?

42.LENGTH OF GUY WIRES A 30-foot tower is to be fastened by three guy wires attached to the top of the tower and to the ground at positions 20 feet from its base. How much wire is needed? Round to the nearest tenth.

43.PICTURE FRAMES After gluing and nailing two pieces of picture frame molding together, a frame maker checks her work by making a diagonal measurement. If the sides of the frame form a right angle, what measurement should the frame maker read on the yardstick?

20 in.

15 in.

44.CARPENTRY The gable end of the roof shown is divided in half by a vertical brace, 8 feet in height. Find the length of the roof line.

8 ft

30 ft

45.BASEBALL A baseball diamond is a square with each side 90 feet long. How far is it from home plate to second base? Round to the nearest

hundredth.

90 ft

90	ft

46.PAPER AIRPLANE The ﬁgure below gives the directions for making a paper airplane from a square piece of paper with sides 8 inches long. Find the length of the plane when it is completed in Step 3. Round to the nearest hundredth.

				Step 2:
8 in.		8 in.		Fold to make
8 in.	Step 1:	8 in.		wing.
				wing.

	Fold
	up.
8 in.		8 in.		Step 3:
8 in.		8 in.		Fold up tip
				Fold up tip
				of wing.
			length

47.FIREFIGHTING The base of the 37-foot ladder shown in the ﬁgure below is 9 feet from the wall. Will the top reach a window ledge that is 35 feet above the ground? Explain how you arrived at your answer.

37 ft

h ft

9 ft

48.WIND DAMAGE A tree was blown over in a wind

	storm. Find the height of	28 ft
	the tree when it was standing	28 ft
	the tree when it was standing
	vertically upright.	45 ft

WRITING

49.State the Pythagorean theorem in your own words.

50.When the lengths of the sides of the triangle shown below are substituted into the equation a2 b2 c2,

the result is a false statement. Explain why. a2 b2 c2

22 42	52	5
		2

4 16	25	4
20	25

9.4 The Pythagorean Theorem

753

51.In the ﬁgure below, equal-sized squares have been

drawn on the sides of right triangle ABC. Explain how this ﬁgure demonstrates that 32 42 52.

B A

52.In the movie The Wizard of Oz, the scarecrow was in search of a brain. To prove that he had found one, he recited the following:

“The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side.”

Unfortunately, this statement is not true. Correct it so that it states the Pythagorean theorem.

REVIEW

Use a check to determine whether the given number is a solution of the equation.

53.2b 3 15, 8

54.5t 4 16, 2

55.0.5x 2.9, 5

56.1.2 x 4.7, 3.5

57.33 x2 30, 6

58.x4 98 100, 8

59.3x 2 4x 5, 12

60.5y 8 3y 2, 5

<<< < Предыдущая 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 5960 / 6760 61 62 63 64 65 66 67 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.12.2018408.58 Кб6antikrizisnoe-upravlenie.doc
#
18.12.2018108.03 Кб6ARHITYeKTURA.doc
#
10.06.20158.32 Mб302aswath_damodaran-investment_philosophies_2012.pdf
#
10.06.201582.94 Кб7audit_risk.doc
#
10.06.20154.17 Mб5BallotingApplicationDocs-SIMSUsersGuide.pdf
#
10.06.201515.55 Mб147basic mathematics for college students.pdf
#
10.06.2015901.06 Кб40Bazy_dannykh_i_znanii_UP_SHirokov_L.A._2000.pdf
#
29.03.20162.45 Mб35Bernd_Fon_Vittenburg_-_Shakh_planete_Zemlya.pdf
#
10.06.201561.93 Кб44bezopasnost.docx
#
10.06.20152.89 Mб84bibliofond_ru_604241.docx
#
10.06.20152.1 Mб30blind_watchmaker.pdf