Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный индустриальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

basic mathematics for college students.pdf

Скачиваний:

147

Добавлен:

10.06.2015

Размер:

15.55 Mб

Скачать

☆

<<< < Предыдущая 43 44 45 46 47 48 49 50 51 52 53 5455 / 6755 56 57 58 59 60 61 62 63 64 65 66 67 > Следующая >>>

688Chapter 8 An Introduction to Algebra

54.THE BERMUDA TRIANGLE The Bermuda Triangle is a triangular region in the Atlantic Ocean where many ships and airplanes have disappeared. The perimeter of the triangle is about 3,075 miles. It is formed by three imaginary lines. The ﬁrst, 1,100 miles long, is from Melbourne, Florida, to Puerto Rico. The second, 1,000 miles long, stretches from Puerto Rico to Bermuda. The third extends from Bermuda back to Florida. Find its length.

WRITING

55.What is the most difﬁcult step of the ﬁve-step problem-solving strategy for you? Explain why it is.

56.Give ten words or phrases that indicate subtraction.

57.What does the word translate mean?

58.Unlike an arithmetic approach, you do not have to determine whether to add, subtract, multiply, or divide to solve the application problems in this section. That decision is made for you when you solve the equation that mathematically describes the situation. Explain.

59.Write a problem that could be represented by the following equation.

Age of father	plus	age of	is	50.
Age of father	plus	son	is	50.
		son
x		x 20		50

60.Write a problem that could be represented by the following equation.

	length			width
2	of a	plus	2	of a	is	600 ft.
	ﬁeld			ﬁeld

2	4x		2	x		600

REVIEW

Find the LCM and the GCF of the given numbers.

61.	100, 120	62.	120, 180
63.	14, 140	64.	15, 300
65.	8, 9, 49	66.	9, 16, 25
67.	66, 198, 242	68.	52, 78, 130

Objectives

S E C T I O N 8.6

1Identify bases and exponents.

2Multiply exponential expressions that have like bases.

3Raise exponential expressions to a power.

4Find powers of products.

Multiplication Rules for Exponents

In this section, we will use the deﬁnition of exponent to develop some rules for simplifying expressions that contain exponents.

1 Identify bases and exponents.

Recall that an exponent indicates repeated multiplication. It indicates how many times the base is used as a factor. For example, 35 represents the product of ﬁve 3’s.

Exponent

5 factors of 3

⎪ ⎪ ⎬ ⎪ ⎪ ⎭

35 3 3 3 3 3

Base

In general, we have the following deﬁnition.

Natural-Number Exponents

A natural-number* exponent tells how many times its base is to be used as a factor.

For any number x and any natural number n,

n factors of x

p xn x x x x

*The set of natural numbers is {1, 2, 3, 4, 5, . . . }.

EXAMPLE 2

8.6 Multiplication Rules for Exponents

689

Expressions of the form xn are called exponential expressions. The base of an exponential expression can be a number, a variable, or a combination of numbers and variables. Some examples are:

105 10 10 10 10 10 y2 y y

( 2s)3 ( 2s)( 2s)( 2s)

84 (8 8 8 8)

The base is 10. The exponent is 5.

Read as “10 to the ﬁfth power.”

The base is y. The exponent is 2. Read as “y squared.”

The base is 2s. The exponent is 3. Read as “negative

2s raised to the third power” or “negative 2s cubed.”

Since the sign is not written within parentheses, the base is 8. The exponent is 4. Read as “the opposite (or the negative) of 8 to the fourth power.”

When an exponent is 1, it is usually not written. For example, 4 41 and x x1.

Caution! Bases that contain a sign must be written within parentheses.

( 2s)3 Exponent

Base

	EXAMPLE 1	Identify the base and the exponent in each expression:
a. 85 b. 7a3		c. (7a)3

Strategy To identify the base and exponent, we will look for the form .

WHY The exponent is the small raised number to the right of the base.

Solution

a.In 85, the base is 8 and the exponent is 5.

b.7a3 means 7 a3. Thus, the base is a, not 7a. The exponent is 3.

c.Because of the parentheses in (7a)3, the base is 7a and the exponent is 3.

Write each expression in an equivalent form using an exponent: a. b b b b b. 5 t t t

Strategy We will look for repeated factors and count the number of times each appears.

WHY We can use an exponent to represent repeated multiplication.

Solution

a.Since there are four repeated factors of b in b b b b, the expression can be written as b4.

b.Since there are three repeated factors of t in 5 t t t, the expression can be written as 5t3.

Self Check 1

Identify the base and the exponent:

a.3y4

b.(3y)4

Now Try Problems 13 and 17

Self Check 2

Write as an exponential expression:

(x + y)(x + y)(x + y)(x + y)(x + y)

Now Try Problems 25 and 29

690	Chapter 8 An Introduction to Algebra

2 Multiply exponential expressions that have like bases.

To develop a rule for multiplying exponential expressions that have the same base, we consider the product 62 63. Since 62 means that 6 is to be used as a factor two times, and 63 means that 6 is to be used as a factor three times, we have

2 factors of 6	3 factors of 6
⎬ ⎭	⎬ ⎭
62 63 6 6	6 6 6
5 factors of 6
⎪ ⎪ ⎬ ⎪ ⎪ ⎭
6 6 6 6 6
65

We can quickly ﬁnd this result if we keep the common base 6 and add the exponents on 62 and 63.

62 63 62 3 65

This example illustrates the following rule for exponents.

Self Check 3

Simplify:

a.78(77)

b.x2x3x

c.(y 1)5(y 1)5

d.(s4t3)(s4t4)

Now Try Problems 33, 35, and 37

Product Rule for Exponents

To multiply exponential expressions that have the same base, keep the common base and add the exponents.

For any number x and any natural numbers m and n,

		xm xn xm n		Read as “x to the mth power times x to the
				nth power equals x to the m plus nth power.”
	EXAMPLE 3		Simplify:

a. 95(96)		b. x3 x4		c. y2y4y	d. (c2d3)(c4d5)

Strategy In each case, we want to write an equivalent expression using one base and one exponent. We will use the product rule for exponents to do this.

WHY The product rule for exponents is used to multiply exponential expressions that have the same base.

Solution

a. 95(96) 95 6 911 Keep the common base, 9, and add the exponents.

Since 911 is a very large number, we will leave the answer in this form. We won’t evaluate it.

Caution! Don’t make the mistake of multiplying the bases when using the product rule. Keep the same base.

95(96) 8111

b.	x3 x4 x3 4 x7 Keep the common base, x, and add the exponents.
c.	y2y4y y2y4y1	Write y as y1.
	y2 4 1	Keep the common base, y, and add the exponents.

d. (c2d3)(c4d5) (c2c4)(d3d5) Use the commutative and associative properties of

multiplication to group like bases together.

(c2 4)(d3 5) Keep the common base, c, and add the exponents.

Keep the common base, d, and add the exponents.

c6d8

8.6 Multiplication Rules for Exponents

691

Caution! We cannot use the product rule to simplify expressions like 32 23, where the bases are not the same. However, we can simplify this expression by doing the arithmetic:

32 23 9 8 72 32 3 3 9 and 23 2 2 2 8.

Recall that like terms are terms with exactly the same variables raised to exactly the same powers. To add or subtract exponential expressions, they must be like terms. To multiply exponential expressions, only the bases need to be the same.

x5	x2	These are not like terms; the exponents are different. We cannot add.
x2 x2	2x2	These are like terms; we can add. Recall that x2 1x2	.
x5 x2	x7	The bases are the same; we can multiply.

3 Raise exponential expressions to a power.

To develop another rule for exponents, we consider (53)4. Here, an exponential expression, 53, is raised to a power. Since 53 is the base and 4 is the exponent, (53)4 can be written as 53 53 53 53. Because each of the four factors of 53 contains three factors of 5, there are 4 3 or 12 factors of 5.

12 factors of 5

(53)4 53 53 53 53 5 5 5 5 5 5 5 5 5 5 5 5 512

⎬ ⎫ ⎭ ⎬ ⎫ ⎭ ⎬ ⎫ ⎭ ⎬ ⎫
53	53	53	53

We can quickly ﬁnd this result if we keep the common base of 5 and multiply the exponents.

(53)4 53 4 512

This example illustrates the following rule for exponents.

Power Rule for Exponents

To raise an exponential expression to a power, keep the base and multiply the exponents.

For any number x and any natural numbers m and n,

(xm)n xm n xmn Read as “the quantity of x to the mth power raised to the nth power equals x to the mnth power.”

The Language of Algebra An exponential expression raised to a power, such as (53)4, is also called a power of a power.

EXAMPLE 4		3	7	2 5	8	8
	Simplify:	a. (2 )		b. [( 6) ]	c. (z )
	Simplify:	a. (2 )		b. [( 6) ]	c. (z )

Strategy In each case, we want to write an equivalent expression using one base and one exponent. We will use the power rule for exponents to do this.

WHY Each expression is a power of a power.

Self Check 4

Simplify:

a.(46)5

b.(y5)2

Now Try Problems 49, 51, and 53

692	Chapter 8 An Introduction to Algebra

Solution

a. (23)7 23 7 221 Keep the base, 2, and multiply the exponents. Since 221 is a very large number, we will leave the answer in this form.

b. [( 6)2]5 ( 6)2 5 ( 6)10 Keep the base, 6, and multiply the exponents. Since ( 6)10 is a very large number, we will leave the answer in this form.

c. (z8)8 z8 8 z64 Keep the base, z, and multiply the exponents.

Self Check 5

Simplify:

a.(a4a3)3

b.(a3)3(a4)2

Now Try Problems 57 and 61

EXAMPLE 5 Simplify: a. (x2x5)2 b. (z2)4(z3)3

Strategy In each case, we want to write an equivalent expression using one base and one exponent.We will use the product and power rules for exponents to do this.

WHY The expressions involve multiplication of exponential expressions that have the same base and they involve powers of powers.

Solution

a. (x2x5)2 (x7)2	Within the parentheses, keep the common base, x, and add the
	exponents: 2 5 7.
x14	Keep the base, x, and multiply the exponents: 7 2 14.
b. (z2)4(z3)3 z8z9	For each power of z raised to a power, keep the base
	and multiply the exponents: 2 4 8 and 3 3 9.
z17	Keep the common base, z, and add the exponents: 8 9 17.
z17	Keep the common base, z, and add the exponents: 8 9 17.

4 Find powers of products.

To develop another rule for exponents, we consider the expression (2x)3, which is a power of the product of 2 and x.

(2x)3 2x 2x 2x	Write the base 2x as a factor 3 times.
(2 2 2)(x x x)	Change the order of the factors and group like bases.
23x3	Write each product of repeated factors in exponential form.
8x3	Evaluate: 23 8.

This example illustrates the following rule for exponents.

Power of a Product

To raise a product to a power, raise each factor of the product to that power. For any numbers x and y, and any natural number n,

(xy)n xnyn

Self Check 6

Simplify:

a.(2t)4

b.(c3d4)6

Now Try Problems 65 and 69

EXAMPLE 6 Simplify: a. (3c)4 b. (x2y3)5

Strategy In each case, we want to write the expression in an equivalent form in which each base is raised to a single power. We will use the power of a product rule for exponents to do this.

WHY Within each set of parentheses is a product, and each of those products is raised to a power.

8.6 Multiplication Rules for Exponents

693

Solution

a. (3c)4 34c4	Raise each factor of the product 3c to the 4th power.
81c4	Evaluate: 34 81.
b. (x2y3)5 (x2)5(y3)5		Raise each factor of the product x2y3 to the 5th power.
x10y15		For each power of a power, keep each base, x and y, and
		multiply the exponents: 2 5 10 and 3 5 15.
		multiply the exponents: 2 5 10 and 3 5 15.

EXAMPLE 7 Simplify: (2a2)2(4a3)3

Strategy We want to write an equivalent expression using one base and one exponent. We will begin the process by using the power of a product rule for exponents.

WHY Within each set of parentheses is a product, and each product is raised to a power.

Solution

(2a2)2(4a3)3 22(a2)2 43(a3)3	Raise each factor of the product 2a2 to the 2nd
	power. Raise each factor of the product 4a3 to
	the 3rd power.
4a4 64a9	Evaluate: 22 4 and 43 64. For each power
	of a power, keep each base and multiply the
	exponents: 2 2 4 and 3 3 9.	1
		1
		64
(4 64)(a4 a9)		64
(4 64)(a4 a9)	Group the numerical factors. Group	4
	the factors that have the same base.	256
256a13	Do the multiplication: 4 64 256. Keep the
	common base a and add the exponents: 4 9 13.

Self Check 7

Simplify: (4y3)2(3y4)3

Now Try Problem 73

The rules for natural-number exponents are summarized as follows.

Rules for Exponents

If m and n represent natural numbers and there are no divisions by zero, then

Exponent of 1	Product rule	Power rule
x1 x	xmxn xm n	(xm)n xmn
	Power of a product
	(xy)n xnyn

ANSWERS TO SELF CHECKS
ANSWERS TO SELF CHECKS
1.	a. base: y, exponent: 4	b. base: 3y, exponent: 4	2. (x y)5	3. a.	715 b. x6
c.	(y 1)10 d. s8t7 4. a.	430 b. y10 5. a. a21	b. a17 6. a.	16t4	b. c18d24
7.	432y18

33. 53 54

694	Chapter 8 An Introduction to Algebra

S E C T I O N 8.6 STUDY SET

VOCABULARY

Fill in the blank.

1. Expressions such as x4, 103, and (5t)2 are called expressions.

2. Match each expression with the proper description.

(a4b2)5

(a8)4

a5 a3

a.Product of exponential expressions with the same base

b.Power of an exponential expression

c.Power of a product

CONCEPTS

Fill in the blanks.

a. (3x)4

b. ( 5y)( 5y)( 5y)

a. x x

b. xmxn

c. (xy)n

d. (ab)c

5.To simplify each expression, determine whether you add, subtract, multiply, or divide the exponents.

a.b6 b9

b.(n8)4

c.(a4b2)5

6.To simplify (2y3z2)4, what factors within the parentheses must be raised to the fourth power?

Simplify each expression, if possible.

7.a. x2 x2

8.a. x2 x

9.a. x3 x2

10.a. 42 24

NOTATION

b. x2 x2 b. x2 x b. x3 x2

b. x3 y2

Complete each solution to simplify each expression.

11.(x4x2)3 ()3

12.(x4)3 (x2)3

x x12 x6

GUIDED PRACTICE

Identify the base and the exponent in each expression.

See Example 1.

13.	43			14.	( 8)2
15.	x5			16.	a	5	b	3

						x

17.	( 3x)2			18.	(2xy)10
19.		1	y6	20.	x4

	3
21.	9m12			22.	3.14r4
23.	(y 9)4			24.	(z 2)3

Write each expression in an equivalent form using an exponent.

See Example 2.

25.m m m m m

26.r r r r r r

27.4t 4t 4t 4t

28.5u( 5u)( 5u)( 5u)( 5u)

29.4 t t t t t

30.5 u u u

31.a a b b b

32.m m m n n

Use the product rule for exponents to simplify each expression. Write the results using exponents. See Example 3.

34. 34 36

35.	a3 a3	36.	m7 m7
37.	bb2b3	38.	aa3a5
39.	(c5)(c8)	40.	(d4)(d20)
41.	(a2b3)(a3b3)	42.	(u3v5)(u4v5)
43.	cd4 cd	44.	ab3 ab4
45.	x2 y x y10	46.	x3 y x y12
47.	m100 m100	48.	n600 n600

Use the power rule for exponents to simplify each expression. Write the results using exponents. See Example 4.

49.	(32)4	50.	(43)3
51.	[( 4.3)3]8	52.	[( 1.7)9]8
53.	(m50)10	54.	(n25)4
55.	(y5)3	56.	(b3)6

Use the product and power rules for exponents to simplify each expression. See Example 5.

57.	(x2x3)5	58.	(y3y4)4
59.	(p2p3)5	60.	(r3r4)2
61.	(t3)4(t2)3	62.	(b2)5(b3)2
63.	(u4)2(u3)2	64.	(v5)2(v3)4

Use the power of a product rule for exponents to simplify each expression. See Example 6.

65.	(6a)2	66.	(3b)3
67.	(5y)4	68.	(4t)4
69.	(3a4b7)3	70.	(5m9n10)2
71.	( 2r2s3)3	72.	( 2x2y4)5

Use the power of a product rule for exponents to simplify each expression. See Example 7.

73.	(2c3)3 (3c4)2	74.	(5b4)2(3b8)2
75.	(10d7)2(4d9)3	76.	(2x7)3(4x8)2

TRY IT YOURSELF

Simplify each expression.
77.	(7a9)2	78.	(12b6)2
79.	t4 t5 t	80.	n4 n n3
81.	y3y2y4	82.	y4yy6
83.	( 6a3b2)3	84.	( 10r3s2)2
85.	(n4n)3(n3)6	86.	(y3y)2(y2)2
87.	(b2b3)12	88.	(s3s3)3
89.	(2b4b)5 (3b)2	90.	(2aa7)3 (3a)3
91.	(c2)3 (c4)2	92.	(t5)2 (t3)3
93.	(3s4t3)3(2st)4	94.	(2a3b5)2(4ab)3
95.	x x2 x3 x4 x5	96.	x10 x9 x8 x7

8.6 Multiplication Rules for Exponents

695

APPLICATIONS

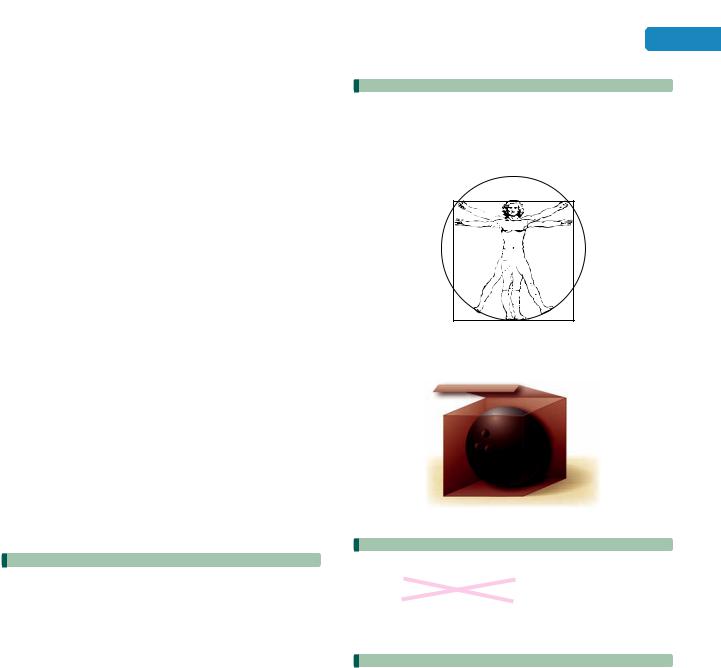
97.ART HISTORY Leonardo da Vinci’s drawing relating a human ﬁgure to a square and a circle is shown. Find an expression for the area of the square if the man’s height is 5x feet.

98.PACKAGING Find an expression for the volume of the box shown below.

6x in.

WRITING

99.Explain the mistake in the following work.

23 22 45 1,024

100.Explain why we can simplify x4 x5, but cannot simplify x4 x5.

REVIEW

101.JEWELRY A lot of what we refer to as gold

jewelry is actually made of a combination of gold and another metal. For example, 18-karat gold is 1824 gold by weight. Simplify this ratio.

102.After evaluation, what is the sign of ( 13)5?

	25
103.	Divide:
			5
104.	How much did the temperature change if it went
	from 4ºF to 17ºF?
	12
105.	Evaluate: 2a				b 3(5)
				3
106.	Solve: 10 x 1
107.	Solve: x 12
108.	Divide:	0

	10

696	Chapter 8 Summary and Review

STUDY SKILLS CHECKLIST

Expressions and Equations

Before taking the test on Chapter 8, make sure that you know the difference between simplifying an expression and solving an equation. Put a checkmark in the box if you can answer “yes” to the statement.

I know that an expression does not contain an = symbol.

Expressions:

2x 3x

4(5y 2)

I know how to simplify expressions by combining like terms.

2x 3x is 5x

I know how to use the distributive property to simplify expressions.

4(5y 2) is 20y 8

I know that an equation contains an = symbol. Equations:

x 5 9

8y 40

I know how to use the addition and subtraction properties of equality to solve equations. If a number is added to (or subtracted from) one side of an equation, the same number must be added to (or subtracted from) the other side.

x5 9

x5 5 9 5 Subtract 5 from both sides.

I know how to use the multiplication and division properties of equality to solve equations. If the one side of an equation is multiplied (or divided) by a number, the other side must be multiplied (or divided) by the same number.

8y 40

8y		40	Divide both sides by 8.
8		8

y 5

C H A P T E R 8	SUMMARY AND REVIEW

S E C T I O N 8.1	The Language of Algebra
S E C T I O N 8.1	The Language of Algebra


DEFINITIONS AND CONCEPTS		EXAMPLES
A variable is a letter (or symbol) that stands		Variables:	x, a, and	y
for a number. Since numbers do not change				3
value, they are called constants.		Constants:	8, 10, 2	3	, and 3.14
value, they are called constants.		Constants:	8, 10, 2	5	, and 3.14
				5
When multiplying a variable by a number, or a		3x means 3 x ab means a b 4rst means 4 r s t
variable by another variable, we can omit the
symbol for multiplication.
Many of the properties that we have seen		The Commutative Property of Addition
while working with whole numbers, integers,			a + b = b + a
fractions, and decimals can be generalized and			a + b = b + a
fractions, and decimals can be generalized and		The Associative Property of Multiplication
stated in symbols using variables.		The Associative Property of Multiplication
stated in symbols using variables.
			(ab)c = a(bc)

Variables and/or numbers can be combined with the operations of addition, subtraction, multiplication, and division to create algebraic expressions.

We often refer to algebraic expressions as simply expressions.

A term is a product or quotient of numbers and/or variables. A single number or variable is also a term. A term such as 4, that consists of a single number, is called a constant term.

Addition symbols separate expressions into parts called terms.

The numerical factor of a term is called the coefﬁcient of the term.

It is important to be able to distinguish between the terms of an expression and the factors of a term.

Key words and key phrases can be translated into algebraic expressions.

To evaluate algebraic expressions, we substitute the values of its variables and apply the rules for the order of operations.

		Chapter 8	Summary and Review	697
Expressions:
5y 7	12 x		8a(b 3)
5y 7			8a(b 3)
5

Terms: 4, y, 6r, –w3, 3.7x5, n3 , –15ab2

Since 6a2 a 5 can be written as 6a2 a ( 5), it has three terms.

	Term	Coefﬁcient

	6a2	6
	a	1
	5	5

x + 6		6x

x is a term.		x is a factor.

5 more than x can be expressed as x 5.

25 less than twice y can be expressed as 2y 25.

One-half of the cost c can be expressed as 12 c.

x2 y2

Evaluate x y for x 2 and y 3.

x2 y2 22 ( 3)2

x y 2 ( 3)

4 9

Substitute 2 for x and 3 for y.

In the numerator, evaluate the exponential expressions. In the denominator, add.

In the numerator, subtract.

Do the division.

a. 16x2 – x + 25

698	Chapter 8 Summary and Review

REVIEW EXERCISES

1.Write each expression without using a multiplication symbol or parentheses.

a.6 b

b.x y z

c.2(t)

2.a. Write the commutative property of addition using the variables c and d.

b.Write the associative property of multiplication using the variables r, s, and t.

3.Determine whether the variable h is used as a term or as a factor.

a. 5h + 9 b. h + 16

4. How many terms does each expression have? a. 3x2 + 2x – 5 b. –12xyz

5.Identify the coefﬁcient of each term of the given expression.

b. x2 y

6.Translate the expression m – 500 into words.

7.Translate each phrase to an algebraic expression.

a.25 more than the height h

b.100 reduced by twice the cutoff score s

c.6 less than one-half of the time t

d.The absolute value of the difference of 2 and the square of a.

8.HARDWARE Refer to the illustration in the next column.

a.Let n represent the length of the nail (in inches). Write an algebraic expression that represents the length of the bolt (in inches).

b.Let b represent the length of the bolt (in inches). Write an algebraic expression that represents the length of the nail (in inches).

4 in.

9.a. CLOTHES DESIGNERS The legs on a pair of pants are x inches long. The designer then lets the hem down 1 inch. Write an algebraic expression that represents the length of the altered pants legs.

b.BUTCHERS A roast weighs p pounds. A butcher trimmed the roast into 8 equal-sized servings. Write an algebraic expression that represents the weight of one serving.

10.SPORTS EQUIPMENT An NBA basketball weighs 2 ounces more than twice the weight of a volleyball.

a.Let x represent the weight of one of the balls. Write an expression for the weight of the other ball.

b.If the weight of the volleyball is 10 ounces, what is the weight of the NBA basketball?

Evaluate each algebraic expression for the given values of the variables.

11.2x2 3x 7 for x 5

12.(x 7)2 for x 1

13.b2 4ac for b 10, a 3, and c 5

14.x z for x 19, y 17, and z 18

S E C T I O N 8.2 Simplifying Algebraic Expressions

DEFINITIONS AND CONCEPTS

We often use the commutative property of multiplication to reorder factors and the associative property of multiplication to regroup factors when simplifying expressions.

EXAMPLES

Simplify:	5(3y) ( 5 3)y 15y
		5		5		1	5
Simplify:	45ba	5	b a 45	5	bb	5 9	5	b 25b
Simplify:	45ba	9	b a 45	9	bb	9		b 25b
						1

The distributive property can be used to remove parentheses:


a(b c) ab ac		a(b c) ab ac

a(b c d) ab ac ad

Like terms are terms with exactly the same variables raised to exactly the same powers.

Simplifying the sum or difference of like terms is called combining like terms. Like terms can be combined by adding or subtracting the coefﬁcients of the terms and keeping the same variables with the same exponents.

Chapter 8 Summary and Review

699

Multiply: 7(x 3) 7 x 7 3

7x 21

Multiply:

0.2(4m 5n 7) 0.2(4m) ( 0.2)(5n) ( 0.2)(7)

0.8m n 1.4

3x and 5x are like terms.

4t3 and 3t2 are unlike terms because the variable t has different exponents.

0.5xyz and 3.7xy are unlike terms because they have different variables.

Simplify:	4a 2a 6a Think: (4 2)a 6a.
Simplify:	5p2 p p2 9p 4p2 8p Think: (5 1)p2 4p2
		and (1 9)p 8p.
Simplify:
Simplify:	2(k 1) 3(k 2) 2k 2 3k 6

k 8

REVIEW EXERCISES

Simplify each expression.

15.	4(7w)	16.	3( 2x)( 4)
17	0.4(5.2ƒ)	18.	7	2	r

			2	7

Use the distributive property to remove parentheses.

19.	5(x 3)		20.	(2x 3 y)
21.	3	(4c 8)	22.	2(3c 7)(2.1)

	4
List the like terms in each expression.
23.	7a 3 9a		24.	2x2 2x 3x2 x

Simplify each expression by combining like terms, if possible.

25.	8p 5p 4p	26.	5m 2 2m 2
27.	n n n n	28.	5(p 2) 2(3p 4)
29.	55.7k2 55.6k2

30.	8a3 4a3 2a 4a3 2a 1
31.	10x 10y				32.	4x3 4x2 4x 4
33.	3	w a	2	wb	34.	36a	1	h	3	b 36a	1	b
	5		5						4		3
						9

35.Write an equivalent expression for the given expression using fewer symbols.

a. 1x	b.	1x
c. 4x ( 1)	d.	4x ( 1)

36.GEOMETRY Write an algebraic expression in simpliﬁed form that represents the perimeter of the triangle.

(x + 7) ft

x ft

(2x – 3) ft

700	Chapter 8 Summary and Review

S E C T I O N 8.3 Solving Equations Using Properties of Equality

DEFINITIONS AND CONCEPTS	EXAMPLES
An equation is a statement indicating that two	Equations:				3			1
expressions are equal. All equations contain	2x 4 10		5(a 4) 11a		3	t 6	t	1
an equal symbol. The equal symbol	2x 4 10		5(a 4) 11a		2	t 6	t	3
separates an equation into two parts: the left
side and the right side.

A number that makes an equation a true	Determine whether 2 is a solution of x 4 3x.
statement when substituted for the variable is	Check: x 4		3x
called a solution of the equation.	Check: x 4		3x
called a solution of the equation.	2 4		3(2)
	2 4		3(2)	Substitute 2 for each x.
		6	6	True

Since the resulting statement, 6 6, is true, 2 is a solution of x 4 3x.

Equivalent equations have the same solutions. x 2 6 and x 8 are equivalent equations because they have the same solution, 8.

To solve an equation isolate the variable on

Solve:

x 5 7

Solve:

c 9 16

one side of the equation by undoing the

x 5 5 7 5

c 9 9 16 9

operations performed on it using properties of

equality.

x 12

c 7

Addition (Subtraction) property of equality: If

the same number is added to (or subtracted

from) both sides of an equation, the result is

an equivalent equation.

Multiplication (Division) property of equality:

Solve:

10y 50

If both sides of an equation are multiplied (or

10y

divided) by the same nonzero number, the

result is an equivalent equation.

b 3(2)

y 5

m 6

REVIEW EXERCISES

Use a check to determine whether the given number is a solution of the equation.

37.	84, x 34 50				38.	3, 5y 2 12
39.	30,	x	6		40.	2,	a2 a 1 0
39.	30,	5	6		40.	2,	a2 a 1 0
		5
41.	3, 5b 2 3b 8				42.	1,	2	12		5

							y 1		y 1
Fill in the blanks.
43.	An			is a statement indicating that two
	expressions are equal.

44.To solve x 8 10 means to ﬁnd all the values of the variable that make the equation a

statement.

Solve each equation. Check the result.

45.	x 9 12		46.	y 32
47.	a 3.7 16.9		48.	100 7 r
49.	120 5c		50.	t		1		3
						2
							2
51.	4	t 12	52.	3			q

	3					2.6

53.	6b 0		54.	15	s 3
				16

Chapter 8 Summary and Review

701

S E C T I O N 8.4

More About Solving Equations

DEFINITIONS AND CONCEPTS

EXAMPLES

A strategy for solving equations:

Solve:

6x + 2 = 14

Simplify each side. Use the distributive

To isolate the variable, we use the order of operations rule in reverse.

property and combine like terms when

• To isolate the variable term, 6x, we subtract 2 from both sides to

necessary.

undo the addition of 2.

Isolate the variable term. Use the addition

• To isolate the variable, x, we divide both sides by 6 to undo the

and subtraction properties of equality.

multiplication by 6.

Isolate the variable. Use the multiplication

and division properties of equality.

2 2

14 2

Subtract 2 from both sides to isolate 6x.

Check the result in the original equation.

Do the subtractions.

Divide both sides by 6 to isolate x.

x 2

The solution is 2. Check by substituting it into the original equation.

When solving equations, we should simplify

Solve:

2(y 2) 4y 11 y

the expressions that make up the left and right

4 4y

11 y

Distribute the multiplication by 2.

sides before applying any properties of

6y 4 11 y

Combine like terms: 2y 4y 6y.

equality.

6y 4 y 11 y y To eliminate y on the right, add y

to both sides.

7y 4 11

Combine like terms.

4 4 11 4

To isolate the variable term 7y,

subtract 4 from both sides.

Simplify each side of the equation.

To isolate y, divide both sides by 7.

y 1

The solution is 1. Check by substituting it into the original equation.

REVIEW EXERCISES

Solve each equation. Check the result.						61.	5(2x 4) 5x 0

55.	5x 4 14		56.	98.6 t 129.2		62.	2(x 5)	5( 3x 4) 3
57.	n	2 4	58.	3	c 10 11	63.	2(m 40)	6m 3(4m 80)
	5			4

59.	12a 9 4a 15		60.	8t 3.2 4t 1.6		64.	8(1.5r 0.5) 3.28

702	Chapter 8 Summary and Review

S E C T I O N 8.5 Using Equations to Solve Application Problems

DEFINITIONS AND CONCEPTS

To solve application problems, use the ﬁvestep problem-solving strategy.

1.Analyze the problem: What information is given? What are you asked to ﬁnd?

2.Form an equation: Pick a variable to represent the numerical value to be found. Translate the words of the problem into an equation.

3.Solve the equation.

4.State the conclusion clearly. Be sure to include the units (such as feet, seconds, or pounds) in your answer.

5.Check the result: Use the original wording of the problem, not the equation that was formed in step 2 from the words.

EXAMPLES

NOBEL PRIZE In 1998, three Americans, Louis Ignarro, Robert Furchgott, and Fred Murad, were awarded the Nobel Prize for Medicine. They shared the prize money equally. If each person received $318,500, what was the amount of the cash award for the Nobel Prize for medicine? (Source: nobelprize.org)

Analyze
• 3 people shared the cash award equally.		Given
•	Each person received $318,500.	Given
•	What was the amount of the cash award?	Find

Form

Let a the amount of the cash award for the Nobel Prize.

Look for a key word or phrase in the problem.

Key Phrase: shared the prize money equally

Translation: division

Translate the words of the problem into an equation.

The amount of			divided	the number of people	was	$318,500.
the cash award			by	that shared it equally

		a		3		318,500
Solve
	a	318,500	We need to isolate a on the left side.

3
	a	3 318,500	To isolate a, undo the division by 3 by			318,500
3 3		3 318,500	multiplying both sides by 3.			318,500
						2 1	3
							3
	a 955,500		Do the multiplication.			955,500

State

The amount of the cash award for the Nobel Prize in Medicine was $955,500.

Check

If the cash prize was $955,500, then the amount that each winner received can be found using division:

318,500 This is the amount each prize winner received.

3 955,500

The result, $955,500, checks.

Chapter 8 Summary and Review

703

The ﬁve-step problem-solving strategy can be

SOUND SYSTEMS A 45-foot-long speaker wire is cut into two

used to solve application problems to ﬁnd two

pieces. One piece is 9 feet longer than the other. Find the length of

unknowns.

each piece of wire.

Analyze

• A 45-foot long wire is cut into two pieces.

Given

• One piece is 9 feet longer than the other.

Given

• What is the length of the shorter piece and the

length of the longer piece of wire?

Find

Form

Since we are told that the length of the longer piece of wire is related

to the length of the shorter piece,

Let x the length of the shorter piece of wire

There is a second unknown quantity. Look for a key phrase to help

represent the length of the longer piece of wire using an algebraic

expression.

Key Phrase: 9 feet longer

Translation: addition

So x + 9 = the length of the longer piece of wire

Now, translate the words of the problem to an equation

The length of the

plus

the length of

45 feet.

shorter piece

the longer piece

x 9

Solve

x x 9 45

We need to isolate x on the left side.

2x 9 45

Combine like terms: x x 2x.

2x 9 9 45 9 To isolate 2x, subtract 9 from both sides.

2x 36

Do the subtraction.

To isolate x, undo the multiplication by 2 by

dividing both sides by 2.

x 18

Do the division.

To ﬁnd the second unknown, we substitute 18 for x in the expression

that represents the length of the longer piece of wire.

x 9 18 9 27

State

The length of the shorter piece of wire is 18 feet and the length of the

longer piece is 27 feet.

704		Chapter 8 Summary and Review

Check

The length of the longer piece of wire, 27 feet, is 9 feet longer than the length of the shorter piece, 18 feet. Adding the two lengths, we get

1827

45 This is the original length of the wire, before It was cut into two pieces.

The results, 18 ft and 27 ft, check.

REVIEW EXERCISES

Form an equation and solve it to answer each question.

65.FINANCING A newly married couple made a $25,000 down payment on a house priced at $122,750. How much did they need to borrow?

66.PATIENT LISTS After moving his ofﬁce, a doctor lost 53 patients. If he had 672 patients left, how many did he have originally?

67.CONSTRUCTION DELAYS Because of a shortage of materials, the ﬁnal cost of a construction project was three times greater than the original estimate. Upon completion, the project cost $81 million. What was the original cost estimate?

68.SOCIAL WORK A human services program assigns each of its social workers a caseload of 80 clients. How many clients are served by 45 social workers?

69.COLD STORAGE A meat locker lowers the temperature of a product 7° Fahrenheit every hour. If freshly ground hamburger is placed in the locker, how long would it take to go from room temperature of 71°F to 29°F?

70.MOVING EXPENSES Tom and his friend split the cost of renting a U-Haul trailer equally. Tom also agreed to pay the $4 to rent a refrigerator dolly. In all, Tom paid $20. What did it cost to rent the trailer?

71.FITNESS The midweek workout for a ﬁtness instructor consists of walking and running. She walks 3 fewer miles than she runs. If her workout covers a total of 15 miles, how many miles does she run and how many miles does she walk?

72.RODEOS Attendance during the ﬁrst day of a two-day rodeo was low. On the second day, attendance doubled. If a total of 6,600 people attended the show, what was the attendance on

the ﬁrst day and what was the attendance on the second day?

73.PARKING LOTS A rectangular-shaped parking lot is 4 times as long as it is wide. If the perimeter of the parking lot is 250 feet, what is its length and width?

74.SPACE TRAVEL The 364-foot-tall Saturn V rocket carried the ﬁrst astronauts to the moon. Its ﬁrst, second, and third stages were 138, 98, and 46 feet tall (in that order). Atop the third stage was a lunar module, and from it extended a 28-foot escape tower. How tall was the lunar module? (Source: NASA)

Chapter 8 Summary and Review

705

S E C T I O N 8.6 Multiplication Rules for Exponents

	DEFINITIONS AND CONCEPTS	EXAMPLES

An exponent indicates repeated multiplication. It tells how many times the base is to be used as a factor.

Exponent		n factors of x
Exponent		n factors of x
		⎪ ⎪ ⎬ ⎪ ⎪ ⎭

	xn x x x p x

Base
Base

Rules for Exponents: If m and n represent integers,

Product rule: xmxn xm n

Power rule: (xm)n xm n xmn

Power of a product rule: (xy)m xmym

To simplify some expressions, we must apply two (or more) rules for exponents.

REVIEW EXERCISES

Identify the base and the exponent in each expression.

26 2 2 2 2 2 2 2 is the base and 6 is the exponent.

( xy)3 ( xy)( xy)( xy) Because of the parentheses, xy is the base and 3 is the exponent.


5t4 5 t t t t		The base is t and 4 is the exponent.
81 8	The base is 8 and 1 is the exponent.
Simplify each expression:
5257 52 7 59		Keep the common base, 5, and add the exponents.
(63)7 63 7 621		Keep the base, 6, and multiply the exponents.
(2p)5 25p5 32p5		Raise each factor of the product 2p to the 5th power.

Simplify: (c2c5)4 (c7)4 Within the parentheses, keep the common base, c, and add the exponents: 2 5 7.

c28	Keep the base, c, and multiply the exponents:
	7 4 28.

Simplify: (t2)4(t3)3 t8t9 For each power of t raised to a power, keep the base and multiply the exponents: 2 4 8 and 3 3 9.

t17 Keep the common base, t, and add the exponents: 8 9 17.

75.Identify the base and the exponent in each expression.

a.	n12	b.	(2x)6
c.	3r4	d.	(y 7)3

76.Write each expression in an equivalent form using an exponent.

a.	m m m m m	b. 3 x x x x
c.	a a b b b b	d. (pq)(pq)(pq)
77. Simplify, if possible.
a.	x2 x2	b.	x2 x2
c.	x x2	d.	x x2

78.Explain each error.

a.32 34 96

b.(32)4 36

Simplify each expression.
79.	74 78	80.	mmnn2
81.	(y7)3	82.	(3x)4
83.	(63)12	84.	b3b4b5
85.	( 16s3)2s4	86.	(2.1x2y)2
87.	[( 9)3]5	88.	(a5)3(a2)4
89.	(2x2x3)3	90.	(m2m3)2(n2n4)3
91.	(3a4)2(2a3)3	92.	x100 x100
93.	(4m3)3(2m2)2	94.	(3t4)3(2t5)2

9. Evaluate

706

C H A P T E R 8 TEST

Fill in the blanks.

1. a. are letters (or symbols) that stand for

numbers.

b. To perform the multiplication 3(x 4), we use the property.

c.Terms such as 7x2 and 5x2, which have the same variables raised to exactly the same power, are

called terms.

d. When we write 4x x as 5x, we say we have like terms.

e. The

of the term 9y is 9.

f.To evaluate y2 9y 3 for y 5, we

5 for y and apply the order of operations rule.

g.Variables and/or numbers can be combined with the operations of arithmetic to create algebraic


h. An			is a statement indicating that two
	expressions are equal.
i.	To	an equation means to ﬁnd all values of
	the variable that make the equation true.
j.	To	the solution of an equation, we
	substitute the value for the variable in the original
	equation and determine whether the result is a
	true statement.

2.Use the following variables to state each property in symbols.

a.Write the associative property of addition using the variables b, c, and d.

b.Write the multiplication property of 1 using the variable t.

3.FISH Refer to the illustration below. Let the variable

srepresent the length of the salmon (in inches). Write an algebraic expression that represents the length of the trout (in inches).

Trout	10 inches

Salmon

4.Translate to symbols

a.2 less than r

b.The product of 3, x, and y

c.The cost c split three equal ways

d.7 more than twice the width w

5.Translate the algebraic expression 34t into words.

6.RETAINING WALLS Refer to the illustration below. Let h = the height of the retaining wall (in feet).

a.Write an algebraic expression to represent the length of the upper base of the brick retaining wall.

b.Write an algebraic expression to represent the length of the lower base of the brick retaining wall.

The length of the upper base is 5 ft less than the height.

Height

The length of the lower base is 3 ft less than twice the height.

7. Determine whether a is used as a factor or as a term. a. 5ab b. 8b a 6

8. Consider the expression x3 8x2 x 6.

a. How many terms does the expression have? b. What is the coefﬁcient of each term?

x 16 for x 4. x

10.Evaluate a2 + 2ab + b2 for a 5 and b 1.

11.Simplify each expression.


a.	9 4s				b.	10(12t)
	2
c. 18a				xb	d.	–4(–6)(–3m)
			3
12. Multiply.
a.	5(5x 1)				b.	6(7 x)
c.	(6y 4)				d.	0.3(2a 3b 7)
e.	1	(2m 8)			f.	(2r 1)9

	2

13. Identify the like terms in the following expression: 12m2 3m 2m2 3

14.Simplify by combining like terms, if possible.

a.20y 8y

b.34a a 7a

c.8b2 29b2

d.9z 6 2z 19

15.Simplify: 4(2y 3) 5(y 3)

16.Use a check to determine whether 7 is a solution of 2y 1 y 8.

Solve each equation and check the result.

17.x 6 10

18.1.8 y 1.3

19.5t 55 q

20.3 27

21.d 13 16

22.78n 21

23.15a 10 20

24.8x 6 3x 7

25.3.6 r 9.8

26.2(4x 1) 3(4 3x) 3x

27.1516x 15 0

28.b 15

Form an equation and solve it to answer each question.

29.HEARING PROTECTION When an airplane mechanic wears ear plugs, the sound intensity that he experiences from a jet engine is only 81 decibels. If the ear plugs reduce sound intensity by 29 decibels, what is the actual sound intensity of a jet engine?

30.PARKING After many student complaints, a college decided to triple the number of parking spaces on campus by constructing a parking structure. That increase will bring the total number of spaces up to 6,240. How many parking spaces does the college have at this time?

	Chapter 8 Test	707
31.	ORCHESTRAS A 98-member orchestra is made up
	of a woodwind section with 19 musicians, a brass
	section with 23 players, a 2-person percussion section,
	and a large string section. How many musicians make
	up the string section of the orchestra?	2009.Grandpa,copyrightImage	Shutterstock.comfromlicenseunderUsed
32.	RECREATION A	2009.Grandpa,copyrightImage	Shutterstock.comfromlicenseunderUsed
32.	RECREATION A
	developer donated a
	large plot of land to a
	city for a park. Half of
	the acres will be used
	for sports ﬁelds. From
	the other half, 4 acres
	will be used for
	parking. This will leave 18 acres for a nature habitat.
	How many acres of land did the developer donate to
	the city?
33.	NUMBER PROBLEM The sum of two numbers is
	63. One number is 17 more than the other. What are
	the numbers?
34.	PICTURE FRAMING A rectangular picture frame
	is twice as long as it is wide. If 144 inches of framing
	material were used to make it, what is the width and
	what is the length of the frame?

35. Identify the base and the exponent of each expression.

a.65

b.7b4

36.Simplify each expression, if possible.

	a.	x2 x2	b.	x2 x2
	c.	x2 x	d.	x2 x
37.	Simplify each expression.
	a.	h2h4	b.	(m10)2
	c.	b2 b b5	d.	(x3)4(x2)3
	e.	(a2b3)(a4b7)	f.	(12a9b)2
	g.	(2x2)3(3x3)3	h. (t2t3)3
38.	Explain what is wrong with the following work:
		54 53 257

<<< < Предыдущая 43 44 45 46 47 48 49 50 51 52 53 5455 / 6755 56 57 58 59 60 61 62 63 64 65 66 67 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.12.2018408.58 Кб6antikrizisnoe-upravlenie.doc
#
18.12.2018108.03 Кб6ARHITYeKTURA.doc
#
10.06.20158.32 Mб301aswath_damodaran-investment_philosophies_2012.pdf
#
10.06.201582.94 Кб7audit_risk.doc
#
10.06.20154.17 Mб4BallotingApplicationDocs-SIMSUsersGuide.pdf
#
10.06.201515.55 Mб147basic mathematics for college students.pdf
#
10.06.2015901.06 Кб40Bazy_dannykh_i_znanii_UP_SHirokov_L.A._2000.pdf
#
29.03.20162.45 Mб35Bernd_Fon_Vittenburg_-_Shakh_planete_Zemlya.pdf
#
10.06.201561.93 Кб44bezopasnost.docx
#
10.06.20152.89 Mб82bibliofond_ru_604241.docx
#
10.06.20152.1 Mб30blind_watchmaker.pdf