112.Explain why multiplying 40.86.2 by the form of 1 shown below moves the decimal points in the dividend,

4.86, and the divisor, 0.2, one place to the right.

4.86 4.86110

0.2 0.2 10

REVIEW

113.a. Find the GCF of 10 and 25.

b.Find the LCM of 10 and 25.

114.a. Find the GCF of 8, 12, and 16.

b.Find the LCM of 8, 12, and 16.

1Write fractions as equivalent terminating decimals.

2Write fractions as equivalent repeating decimals.

3Round repeating decimals.

4Graph fractions and decimals on a number line.

5Compare fractions and decimals.

6Evaluate expressions containing fractions and decimals.

7Solve application problems involving fractions and decimals.

Fractions and Decimals

In this section, we continue to explore the relationship between fractions and decimals.

1 Write fractions as equivalent terminating decimals.

A fraction and a decimal are said to be equivalent if they name the same number. Every fraction can be written in an equivalent decimal form by dividing the numerator by the denominator, as indicated by the fraction bar.

Writing a Fraction as a Decimal

To write a fraction as a decimal, divide the numerator of the fraction by its denominator.

Self Check 1

Write each fraction as a decimal. 1

a. 2

3

b.16

9

c.2

Now Try Problems 15, 17, and 21

Strategy We will divide the numerator of each fraction by its denominator. We will continue the division process until we obtain a zero remainder.

WHY We divide the numerator by the denominator because a fraction bar indicates division.

Solution

0.75

4 3.00

2 8T 2020 0

Write a decimal point and two additional zeros to the right of 3.

The remainder is 0.

20

16

40

40

0

The remainder is 0.

3.5

2 7.0

6

1 0

1 0

0

Write a decimal point and one additional zero to the right of 7.

The remainder is 0.

Self Check 2

Write each fraction as a decimal using multiplication by a form of 1:

2

a. 5

8

b. 25

Now Try Problems 27 and 29

Self Check 3

Write the mixed number 31720 in decimal form.

Now Try Problem 37

Some fractions can be written as decimals using an alternate approach. If the denominator of a fraction in simplified form has factors of only 2’s or 5’s, or a combination of both, it can be written as a decimal by multiplying it by a form of 1. The objective is to write the fraction in an equivalent form with a denominator that is a power of 10, such as 10, 100, 1,000, and so on.

Strategy We will multiply 45 by 22 and we will multiply 1140 by 2525 .

WHY The result of each multiplication will be an equivalent fraction with a denominator that is a power of 10. Such fractions are then easy to write in decimal form.

Solution

a.Since we need to multiply the denominator of 45 by 2 to obtain a denominator of 10, it follows that 22 should be the form of 1 that is used to build 45 .

10Multiply the denominators.

0.8 Write the fraction as a decimal.

b.Since we need to multiply the denominator of 1140 by 25 to obtain a denominator of 1,000, it follows that 2525 should be the form of 1 that is used to build 1140 .

Mixed numbers can also be written in decimal form.

Strategy We need only find the decimal equivalent for the fractional part of the mixed number.

Solution To write 167 as a fraction, we find 7 16.

0.4375

16 7.0000 Write a decimal point and four additionl zeros to the right of 7.

6 4

6048

120112

8080

Since the whole-number part of the decimal must be the same as the whole-number part of the mixed number, we have:

We would have obtained the same result if we changed 5 167 to the improper fraction 8716 and divided 87 by 16.

Strategy We will divide the numerator of the fraction by its denominator and watch for a repeating pattern of nonzero remainders.

WHY Once we detect a repeating pattern of remainders, the division process can stop.

Solution 125 means 5 12.

0.4166

12 5.0000 Write a decimal point and four additional zeros to the right of 5.

4 8

2012

80

72

80

It is apparent that 8 will continue to reappear as the remainder. Therefore,72 6 will continue to reappear in the quotient. Since the repeating pattern is

8 now clear, we can stop the division.

We can use three dots to show that a repeating pattern of 6’s appears in the quotient:

125 0.416666 . . .

Or, we can use an overbar to indicate the repeating part (in this case, only the 6), and write the decimal equivalent in more compact form:

5

12 0.416

Strategy To find the decimal equivalent for 116 , we will first find the decimal equivalent for 116 . To do this, we will divide the numerator of 116 by its denominator and watch for a repeating pattern of nonzero remainders.

Self Check 4

Write 121 as a decimal.

Now Try Problem 41

Self Check 5

Write 1333 as a decimal.

Now Try Problem 47

0.54545

11 6.00000

5 5

50

44

60

55

50

44

60

55

5

Write a decimal point and five additional zeros to the right of 6.

It is apparent that 6 and 5 will continue to reappear as remainders. Therefore, 5 and 4 will continue to reappear in the quotient. Since the repeating pattern is now clear, we can stop the division process.

Strategy We will use the methods of this section to divide to the thousandths column.

WHY To round to the hundredths column, we need to continue the division process for one more decimal place, which is the thousandths column.

Solution 13 means 1 3.

0.333

3 1.000 Write a decimal point and three additional zeros to the right of 1.

9

10

9

10

9

1 The division process can stop. We have divided to the thousandths column.

After dividing to the thousandths column, we round to the hundredths column.

The rounding digit in the hundredths column is 3.

The test digit in the thousandths column is 3.

0.333 . . .

Since 3 is less than 5, we round down, and we have

1

3 0.33 Read as “is approximately equal to.”

Strategy We will use the methods of this section to divide to the ten-thousandths column.

WHY To round to the thousandths column, we need to continue the division process for one more decimal place, which is the ten-thousandths column.

Solution 27 means 2 7.

0.2857

7 2.0000 Write a decimal point and four additional zeros to the right of 2.

1 4

6056

4035

50

49

1The division process can stop.

We have divided to the ten-thousandths column.

After dividing to the ten-thousandths column, we round to the thousandths column.

The rounding digit in the thousandths column is 5.

The test digit in the ten-thousandths column is 7.

0.2857

Since 7 is greater than 5, we round up, and 27 0.286.

Self Check 6

Write 49 as a decimal and round to the nearest hundredth.

Now Try Problem 51

Self Check 7

Write 247 as a decimal and round to the nearest thousandth.

Now Try Problem 61

Self Check 8

Place an , , or an symbol in the box to make a true statement:

3

a. 8 0.305

Now Try Problems 67, 69, and 71

Using Your CALCULATOR The Fixed-Point Key

After performing a calculation, a scientific calculator can round the result to a given decimal place. This is done using the fixed-point key. As we did in Example 7, let’s find the decimal equivalent of 27 and round to the nearest thousandth. This time, we will use a calculator.

First, we set the calculator to round to the third decimal place (thousandths)

Thus, 27 0.286. To round to the nearest tenth, we would fix 1; to round to the nearest hundredth, we would fix 2; and so on. After using the FIX feature, don’t forget to remove it and return the calculator to the normal mode.

Graphing calculators can also round to a given decimal place. See the owner’s manual for the required keystrokes.

4 Graph fractions and decimals on a number line.

A number line can be used to show the relationship between fractions and their decimal equivalents. On the number line below, sixteen equally spaced marks are used to scale from 0 to 1. Some commonly used fractions that have terminating decimal equivalents are shown. For example, we see that 18 0.125 and 1316 0.8125.

On the next number line, six equally spaced marks are used to scale from 0 to 1. Some commonly used fractions and their repeating decimal equivalents are shown.

5 Compare fractions and decimals.

To compare the size of a fraction and a decimal, it is helpful to write the fraction in its equivalent decimal form.

Strategy In each case, we will write the given fraction as a decimal.

WHY Then we can use the procedure for comparing two decimals to determine which number is the larger and which is the smaller.

Solution

a. To write 45 as a decimal, we divide 4 by 5.

0.8

5 4.0 Write a decimal point and one additional zero to the right of 4.

4 0

0

Thus, 45 0.8.

To make the comparison of the decimals easier, we can write one zero after 8 so that they have the same number of digits to the right of the decimal point.

0. 8 0 This is the decimal equivalent for 54 .

0. 9 1

As we work from left to right, this is the first column in which the digits differ. Since 8 9, it follows that 0.80 45 is less than 0.91, and we can write 45 0.91.

b.In Example 6, we saw that 13 0.3333 . . . . To make the comparison of these repeating decimals easier, we write them so that they have the same number of

digits to the right of the decimal point.

As we work from left to right, this is the first column in which the digits differ. Since 5 3, it follows that 0.3555 . . . 0.35 is greater than 0.3333 . . . 13 , and we can write 0.35 13 .

c. To write 94 as a decimal, we divide 9 by 4.

2.25

4 9.00 Write a decimal point and two additional zeros to the right of 9.

8

1 0

8 20

20 0

From the division, we see that 94 2.25.

EXAMPLE 9 Write the numbers in order from smallest to largest: 2.168, 2 16 , 209

Strategy We will write 216 and 209 in decimal form.

WHY Then we can do a column-by-column comparison of the numbers to determine the largest and smallest.

Solution From the number line on page 378, we see that 16 0.16. Thus, 216 2.16. To write 209 as a decimal, we divide 20 by 9.

2.222

18 20

18 20

18 20

18 2

Thus, 209 2.222 . . . .

Self Check 9

Write the numbers in order from smallest to largest: 1.832, 95 , 156

Now Try Problem 75

Self Check 10

Evaluate by working in terms of fractions: 0.53 16

Now Try Problem 79

Self Check 11

Estimate the result by working in terms of decimals: 0.53 16

Now Try Problem 87

Evaluate: a45b(1.35) (0.5)2

Strategy We will find the decimal equivalent of 45 and then evaluate the expression in terms of decimals.

WHY Its easier to perform multiplication and addition with the given decimals than it would be converting them to fractions.

Solution We use division to find the decimal equivalent of 45 .

0.8

5 4.0

Write a decimal point and one additional zero to the right of the 4.

4 0 0

Now we use the order of operation rule to evaluate the expression.

Self Check 12

Evaluate: ( 0.6)2 (2.3)a18b

Now Try Problem 99

7 Solve application problems involving fractions and decimals.

Form To find the total cost of each item, multiply the number of pounds purchased by the price per pound.

Self Check 13

DELICATESSENS A shopper purchased 23 pound of Swiss cheese, priced at $2.19 per pound, and 34 pound of sliced turkey, selling for $6.40 per pound. Find the total cost of these items.

Now Try Problem 111

The total cost of the items

The total cost of the items

8.Sometimes, when finding the decimal equivalent of a fraction, the division process ends because a remainder of 0 is obtained. We call the resulting

9.Sometimes, when we are finding the decimal equivalent of a fraction, the division process never gives a remainder of 0. We call the resulting decimal a

decimal.

10.If the denominator of a fraction in simplified form has factors of only 2’s or 5’s, or a combination of both, it can be written as a decimal by multiplying it by a form of .

11.a. Round 0.3777 . . . to the nearest hundredth.

b.Round 0.212121 . . . to the nearest thousandth1 . 2

12.a. When evaluating the expression 0.25 2.3 25 2, would it be easier to work in terms of fractions or

decimals?

b.What is the first step that should be performed to evaluate the expression?

NOTATION

13. Write each decimal in fraction form.

14.Write each repeating decimal in simplest form using an overbar.

GUIDED PRACTICE

Write each fraction as a decimal. See Example 1.

Write each fraction as a decimal using multiplication by a form of 1. See Example 2.

Write each mixed number in decimal form. See Example 3.

Write each fraction as a decimal. Use an overbar in your answer.

See Example 4.

Write each fraction as a decimal. Use an overbar in your answer.

See Example 5.

Write each fraction in decimal form. Round to the nearest hundredth. See Example 6.

Write each fraction in decimal form. Round to the nearest thousandth. See Example 7.

Graph the given numbers on a number line. See Objective 4.

63. 134 , 0.75, 0.6, 3.83

−5 − 4 −3 −2 −1 0 1 2 3 4 5

64. 278 , 2.375, 0.3, 4.16

−5 − 4 −3 −2 −1 0 1 2 3 4 5

65. 3.875, 3.5, 0.2, 145

−5 − 4 −3 −2 −1 0 1 2 3 4 5

66. 1.375, 417 , 0.1, 2.7

−5 − 4 −3 −2 −1 0 1 2 3 4 5

Place an , , or an symbol in the box to make a true statement. See Example 8.

Write the numbers in order from smallest to largest.

See Example 9.

86

77.0.81, 9 , 7

1

78. 0.19, 11 , 0.1

Evaluate each expression. Work in terms of fractions.

See Example 10.

Estimate the value of each expression. Work in terms of decimals. See Example 11.

Evaluate each expression. Work in terms of decimals.

See Example 12.

95.(3.5 6.7)a 14b

96.a 58ba5.3 3 109 b

2

97. a15b (1.7)

2

98. (2.35)a25b

2

99. 7.5 (0.78)a12b

2

100. 8.1 a34b (0.12)

101. 38 (3.2) a4 12ba 14b

102. ( 0.8)a14b a15b(0.39)

APPLICATIONS

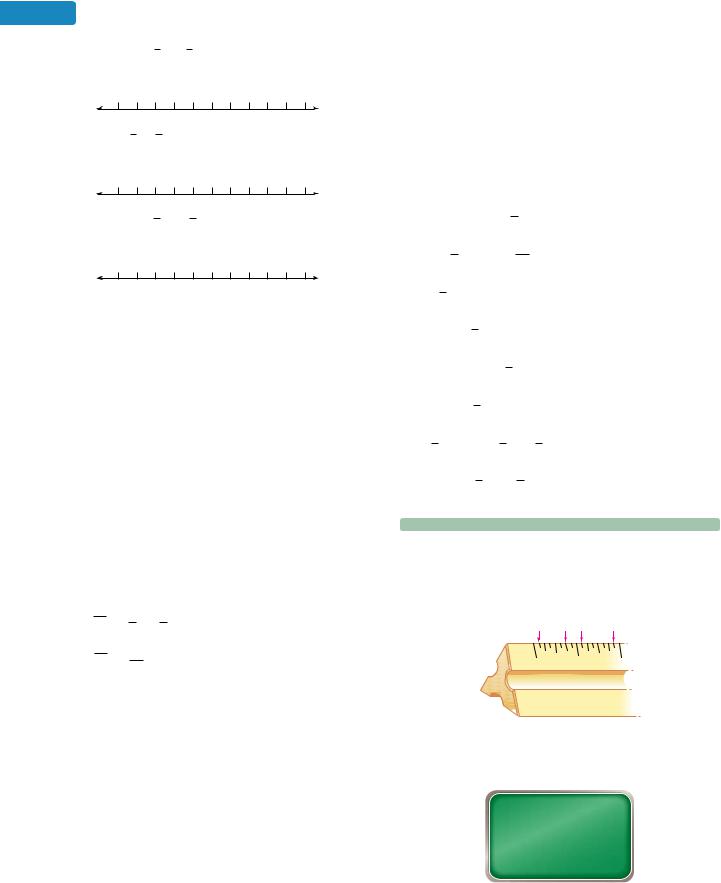
103.DRAFTING The architect’s scale shown below has several measuring edges. The edge marked 16 divides each inch into 16 equal parts. Find the

decimal form for each fractional part of 1 inch that is highlighted with a red arrow.

16

104.MILEAGE SIGNS The freeway sign shown below gives the number of miles to the next three exits. Convert the mileages to decimal notation.

105.GARDENING Two brands of replacement line for a lawn trimmer shown below are labeled in different ways. On one package, the line’s thickness is expressed as a decimal; on the other, as a fraction. Which line is thicker?

106.AUTO MECHANICS While doing a tune-up, a mechanic checks the gap on one of the spark plugs

of a car to be sure it is firing correctly. The owner’s manual states that the gap should be 1252 inch. The gauge the mechanic uses to check the gap is in

decimal notation; it registers 0.025 inch. Is the spark plug gap too large or too small?

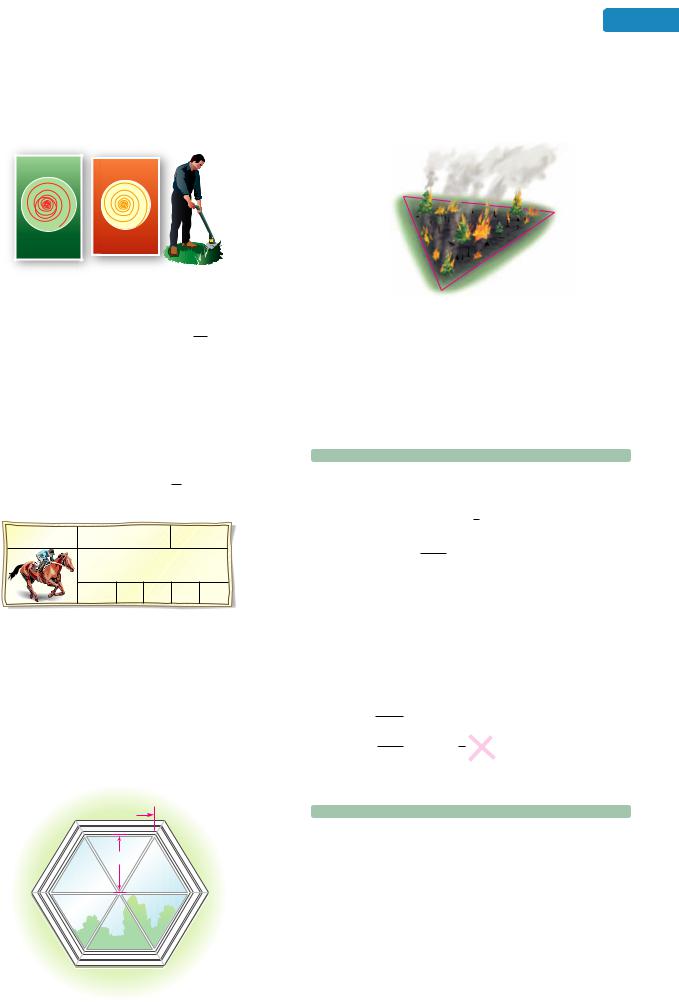
107.HORSE RACING In thoroughbred racing, the time a horse takes to run a given distance is

measured using fifths of a second. For example, :232 (read “twenty-three and two”) means 2325 seconds. The illustration below lists four split times for a horse named Speedy Flight in a 1161 -mile race. Express each split time in decimal form.

108.GEOLOGY A geologist weighed a rock sample at

the site where it was discovered and found it to weigh 1778 lb. Later, a more accurate digital scale in the laboratory gave the weight as 17.671 lb. What is

the difference in the two measurements?

109.WINDOW REPLACEMENTS The amount of sunlight that comes into a room depends on the area of the windows in the room. What is the area of the

window shown below? (Hint: Use the formula

A 12 bh.)

6 in.

5.2 in.

110.FORESTRY A command post asked each of three fire crews to estimate the length of the fire line they were fighting. Their reports came back in different forms, as shown. Find the perimeter of the fire. Round to the nearest tenth.

North flank 1.9 mi

West flank

1

1– mile East flank

8

2

1– mile

3

111.DELICATESSENS A shopper purchased 23 pound of green olives, priced at $4.14 per pound, and 34 pound of smoked ham, selling for $5.68 per pound. Find the total cost of these items.

112.CHOCOLATE A shopper purchased 34 pound

of dark chocolate, priced at $8.60 per pound, and 13 pound of milk chocolate, selling for $5.25 per pound. Find the total cost of these items.

WRITING

113.Explain the procedure used to write a fraction in decimal form.

114.How does the terminating decimal 0.5 differ from the repeating decimal 0.5?

115.A student represented the repeating decimal 0.1333 . . . as 0.1333. Is this the best form? Explain why or why not.

116.Is 0.10100100010000 . . . a repeating decimal? Explain why or why not.

117.A student divided 19 by 25 to find the decimal equivalent of 1925 to be 0.76. Explain how she can check this result.

118.Explain the error in the following work to find the decimal equivalent for 56 .

1.2

5 6.0

5

1010 0

Thus,

REVIEW

119.Write each set of numbers.

a.the first ten whole numbers

b.the first ten prime numbers

c.the integers

120.Give an example of each property.

a.the commutative property of addition

b.the associative property of multiplication

c.the multiplication property of 1