Square Roots

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный индустриальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

basic mathematics for college students.pdf

Скачиваний:

149

Добавлен:

10.06.2015

Размер:

15.55 Mб

Скачать

☆

<<< < Предыдущая 23 24 25 26 27 28 29 30 31 32 33 3435 / 6735 36 37 38 39 40 41 42 43 44 45 46 47 > Следующая >>>

radical expression.

386 Chapter 4 Decimals

Objectives

S E C T I O N 4.6

1Find the square root of a perfect square.

Approximate

with the decimal 0.17.

Do the addition.

2Find the square root of fractions and decimals.

3Evaluate expressions that contain square roots.

4Evaluate formulas involving square roots.

We have discussed the relationships between addition and subtraction and between multiplication and division. In this section, we explore the relationship between raising a number to a power and ﬁnding a root. Decimals play an important role in this discussion.

5 Approximate square roots.

Self Check 1

Find the two square roots of 64.

Now Try Problem 21

1 Find the square root of a perfect square.

When we raise a number to the second power, we are squaring it, or ﬁnding its square.

The square of 6 is 36, because 62 36.

The square of 6 is 36, because ( 6)2 36.

The square root of a given number is a number whose square is the given number. For example, the square roots of 36 are 6 and 6, because either number, when squared, is 36.

Every positive number has two square roots. The number 0 has only one square root. In fact, it is its own square root, because 02 0.

Square Root

A number is a square root of a second number if the square of the ﬁrst number equals the second number.

EXAMPLE 1 Find the two square roots of 49.

Strategy We will ask “What positive number and what negative number, when squared, is 49?”

WHY The square root of 49 is a number whose square is 49.

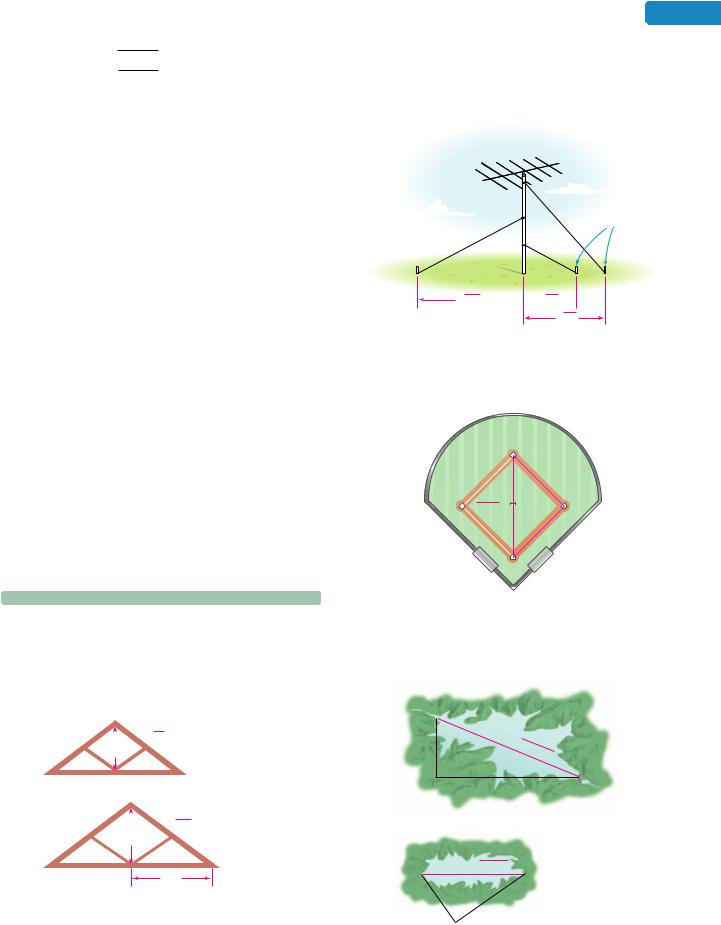
Solution

7 is a square root of 49 because 72 49

and

7 is a square root of 49 because ( 7)2 49.
In Example 1, we saw that 49 has two square roots—one positive and one
negative. The symbol 1	is called a radical symbol and is used to indicate a positive

square1 root of a nonnegative number. When reading this symbol, we usually drop the word positive and1simply say square root. Since 7 is the positive square root of 49, we can write

49 7 49 represents the positive number whose square is 49.

Read as “the square root of 49 is 7.”

When a number, called the radicand, is written under a radical symbol, we have a

Radical symbol
		Radicand

	149
	b
	b

Radical expression

Some 1other examples1 of radical1 expressions1 are: 36 100 144 81

To1 evaluate (or simplify) a radical expression like those shown above,1we need to ﬁnd the positive square root of the radicand. For example, if we evaluate 36 (read as “the square root of 36”), the result is

36 6

because 62 36.


Caution! Remember that the radical symbol asks you to ﬁnd only the
positive square root of the radicand. It is incorrect, for example, to say that
	1			is 6 and 6
			36
The symbol 1		is used to indicate the negative square root of a positive

number.1It is the opposite of the positive square1 root. Since –6 is the negative square root of 36, we can write

36 6 Read as “the negative square root of 36 is 16” or “the opposite of the square root of 36 is 6.” 36 represents the negative number whose square is 36.

If the number under the radical symbol is 0, we have 0 0.

Numbers, such as 36 and 49, that are squares of whole numbers, are called perfect squares. To evaluate square root radical expressions, it is helpful to be able to identify perfect square radicands. You need to memorize the following list of perfect squares, shown in red.

Perfect Squares

0	02	16 42	64	82	144 122
1	12	25 52	81	92	169 132
4	22	36 62	100	102	196 142
9	32	49 72	121	112	225 152

A calculator is helpful in ﬁnding the square root of a perfect square that is larger

than 225.
EXAMPLE 2 Evaluate each square root: a.	181 b. 1100

WHY The radical symbol 1 indicates that the positive square root of the
number written under it should be found.
Solution
a. 1	9 Ask: What positive number, when squared, is 81?

Strategy In each case, we will determine what positive number, when squared, produces the radicand.

181 1 The answer is 9 because 92 81.

b. 100 is the opposite (or negative) of the square root of 100. Since 100 10, we have

100 10

4.6 Square Roots

387

Self1 Check 2

Evaluate1 each square root: a. 144

b. 81

Now Try Problems 25 and 29

Ask: What positive decimal, when squared, is 0.81? The answer is 0.9 because (0.9)2 0.81.

Ask: What positive fraction,1 2when squared, is The answer is 85 because 85 2 6425.

6425 ?

EXAMPLE 3

b. 10.81

388	Chapter 4 Decimals

Caution! Radical expressions such as			1 81
1 36	1 100	1 144

do1 not represent real numbers,1because there are no real1 numbers1that when squared give a negative number.

Be careful to note the difference between expressions such as 36 and36. We have seen that 36 is a real number: 36 6. In contrast,36 is not a real number.

Using Your CALCULATOR Finding a square root

We use the

key (square root key) on a scientiﬁc calculator to ﬁnd

square roots.

For

example, to ﬁnd 1

we enter these numbers and press

729,

these keys.

729

that 1

We have

found

27. To check this result, we need to square 27.

729

Some calculator models require keystrokes of 2nd and then 1 followed by the radicand to ﬁnd a square root.

This can be done by entering 27 and pressing the x2 key. We obtain 729. Thus, 27 is the square root of 729.

Self Check 3

a.116

b.0.04Evaluate:B

Now Try Problems 37 and 43

2 Find the square root of fractions and decimals.

So far, we have found square roots of whole numbers.We can also ﬁnd square roots of fractions and decimals.

Evaluate each square root: a. B25 64

WHY The radical symbol 1 indicates that the positive square root of the numberB written under it should be found.

Strategy In each case, we will determine what positive number, when squared, produces the radicand.

Solution a. 12564 58

b. 0.81 0.9

3 Evaluate expressions that contain square roots.

In Chapters 1, 2, and 3, we used the order of operations rule to evaluate expressions that involve more than one operation. If an expression contains any square roots, they are to be evaluated at the same stage in your solution as exponential expressions. (See step 2 in the familiar order of operations rule on the next page.)

Evaluate each square root ﬁrst.

Order of Operations

1. Perform all calculations within parentheses and other grouping symbols following the order listed in Steps 2–4 below, working from the innermost pair of grouping symbols to the outermost pair.


2.		Evaluate all exponential expressions and square roots.
3.		Perform all multiplications and divisions as they occur from left to right.
4.		Perform all additions and subtractions as they occur from left to right.
	EXAMPLE 4		Evaluate: a. 1		1		b. 1		1

				64		9		25		225

Strategy We will scan the expression to determine what operations need to be performed. Then we will perform those operations, one-at-a-time, following the order of operations rule.

WHY If we don’t follow the correct order of operations, the expression can have more than one value.

Solution1 Since1 the expression does not contain any parentheses, we begin with step 2 of the rules for the order of operations: Evaluate all exponential expressions and any square roots.

a. 64 9 8 3


11						Do the addition.
b. 1			1		5 15		Evaluate each square root ﬁrst.
b. 1		25	1	225	5 15		Evaluate each square root ﬁrst.
					20 Do the subtraction.
					20 Do the subtraction.
	EXAMPLE 5					Evaluate:	a. 61		b. 5	1		3	1

								100			16			9

Strategy We will scan the expression to determine what operations need to be performed. Then we will perform those operations, one-at-a-time, following the order of operations rule.

WHY If we don’t follow the correct order of operations, the expression can have more than one value.

Solution Since the expression does not contain any parentheses, we begin with step 2 of the rules for the order of operations: Evaluate all exponential expressions and any square roots.


a. We note that 61									means 6 1
a. We note that 61								100	means 6 1		100.
61					6(10) Evaluate the square root ﬁrst.
61				100	6(10) Evaluate the square root ﬁrst.
60									Do the multiplication.
b. 51			31				5(4) 3(3) Evaluate each square root ﬁrst.
b. 51		16	31			9	5(4) 3(3) Evaluate each square root ﬁrst.
20 9											Do the multiplication.
11											Do the addition.	1
11											Do the addition.
	EXAMPLE 6							Evaluate:		12 3 C32 (4 1)				D

													36

Strategy We will work within the parentheses ﬁrst and then within the brackets. Within each set of grouping symbols, we will follow the order of operations rule.

4.6 Square Roots

389

Self1 Check14

Evaluate:1 1

a. 121 1

b. 9 196

Now Try Problems 49 and 53

Self1Check 5

Evaluate:1 1

a. 8 121

b. 6 25 2 36

Now Try Problems 57 and 61

Self Check 6

Evaluate:	14 D
10 4C22 (3 2)

Now Try Problems 65 and 69

WHY By the order of operations rule, we must work from the innermost pair of grouping symbols to the outermost.

EXAMPLE 7

390	Chapter 4 Decimals

Self Check 72

Evaluate a c2 b2 for c 17 and b 15.

Now Try Problem 81

n 1n

113.317

123.464

133.606

143.742

153.873

164.000

174.123

184.243

194.359

204.472

Solution
12 3 C32 (4 1)1		D 12	3 C32 31		D	Do the subtraction within the
12 3 C32 (4 1)1	36	D 12	3 C32 31	36	D	Do the subtraction within the
						parentheses.
12			3[9 3(6)]			Within the brackets, evaluate the
						exponential expression and the
						square root.
12			3[9 18]			Do the multiplication within the
						brackets.
12			3[ 9]			Do the subtraction within the
						brackets.
12			( 27)			Do the multiplication.
15						Do the addition.
15						Do the addition.

4 Evaluate formulas involving square roots.

To evaluate formulas that involve square roots, we replace the letters with speciﬁc numbers and the then use the order2of operations rule.

Evaluate c a2 b2 for a 3 and b 4.

Strategy In the given formula, we will replace the letter a with 3 and b with 4. Then we will use the order of operations rule to ﬁnd the value of the radicand.

WHY We need to know the value of the radicand before we can ﬁnd its square root.

Solution
	2
c			a2 b2	This is the formula to evaluate.
	32 42			Replace a with 3 and b with 4.
	1			Evaluate the exponential expressions.
		9 16
		25		Do the addition.
5				Evaluate the square root.

perfect square, we can use the 1 key on a calculator1 or a table of square roots to ﬁnd its approximate square root. For example, to ﬁnd 17 using a scientiﬁc calculator,

5 Approximate square roots.

In Examples 2–7, we have found square roots of perfect squares. If a number is not a

we enter	7 and press the square root key:
17	1
17	1
The display reads
4.123105626		1
This result is an approximation, because the exact value of				is a nonterminating
This result is an approximation, because the exact value of			17	is a nonterminating

decimal1 that never repeats. If we round to the nearest thousandth, we have 17 4.123 Read as “is approximately equal to.”

To check this approximation, we square 4.123. (4.123)2 16.999129

Since the result is close to 17, we know that 17 4.123 .

A portion of the table of square roots from Appendix III on page A-00 is shown1 in the margin on the previous page. The table gives decimal approximations of square roots of whole numbers that are not perfect squares.To ﬁnd an approximation of 17

to the nearest thousandth, we locate			7 in the n-column of the table and scan directly
right, to the 1		-column, to ﬁnd that	1		4.123.
	n			17


	EXAMPLE 8	Use a calculator to approximate each square root. Round to
the nearest hundredth.			a. 1		b. 1		c. 1
the nearest hundredth.			a. 1	373	b. 1	56.2	c. 1	0.0045
Strategy We will identify the radicand and ﬁnd the square root using the 1

key. Then we will identify the digit in the thousandths column of the display.

WHY To round to the hundredths1 column, we must determine whether the digit in the thousandths1column is less than 5, or greater than or equal to 5.

Solution 1

a. From the calculator,1 we get 373 19.31320792. Rounded to the nearest hundredth, 373 19.31. 1

b. From the calculator,1 we get 56.2 7.496665926. Rounded to the nearest hundredth, 56.2 7.50.

c. From the calculator, we get 0.0045 0.067082039. Rounded to the nearest hundredth, 0.0045 0.07.

4.6 Square Roots

391

Self Check 8

Use1a calculator to approximate each square root. Round to the nearest hundredth.

a. 153 b. 607.8

c. 0.076

Now Try Problems 87 and 91

ANSWERS TO SELF CHECKS

1.	8 and 8	2.	a.	12 b. 9 3.	a.	4	b. 0.2 4. a. 12 b. 17 5. a. 88 b. 18
	34 7. 8			12.37 b. 24.65		7	0.28
6.	34 7. 8	8.	a.	12.37 b. 24.65	c.		0.28

S E C T I O N

4.6

STUDY SET

VOCABULARY

Fill in the blanks.

When we raise a number to the second power, we are

squaring it, or ﬁnding its

The square

of a given number is a number

whose square is the given number.

The symbol 1

is called a

symbol.

Label the radicand, the radical expression, and the

164

radical symbol in the illustration below.

Whole numbers such as 36 and 49, that are squares of

whole numbers, are called

squares.

The exact value of 1

is a

decimal

that never repeats.

CONCEPTS

Fill in the blanks.
7.	a.	The square of 5 is										, because 52											.
7.	a.	The square of 5 is										, because 52											.
						1													1		2
						1													1		2
	b.	The square of						is				, because a								b						.
	b.	The square of						is				, because a							4	b						.
						4													4
8. Complete the list of perfect squares: 1, 4,
8. Complete the list of perfect squares: 1, 4,																								, 16,			,
	36, 49, 64,					, 100,					, 144,							, 196,							.
	36, 49, 64,					, 100,					, 144,							, 196,							.
		1			7, because						2 49.
9.	a.	1	49		7, because						2 49.
	b.			2, because						2 4.
	b.		4	2, because						2 4.
															2
		9							3							9
		9							3							9
10.	a.	B				, because a								b			.
10.	a.	B	16			, because a							4	b			.
	a.														b.	160
	a.	11													b.	160
	b.	10.16					, because (0.4)2									0.16.
11. Evaluate each square root.

12. Evaluate each square root.
		1							1												1
	a.	1	121					b.	1		144								c.		1	169
	d.	196						e.	225

392	Chapter 4 Decimals

13.In what1step of the1order of operations rule are square roots to be evaluated?

14.Graph 9 and 4 on a number line.


							−5 − 4 −3 −2 −1 0 1 2 3 4 5
15.		Graph 1									and				1			on a number line. (Hint: Use a
15.		Graph 1							3		and				1	7		on a number line. (Hint: Use a
		calculator or square root table to approximate each
		square root ﬁrst.)


							−5 − 4 −3 −2 −1 0 1 2 3 4 5
16.		a.	Between what two whole numbers would 1
16.		a.	Between what two whole numbers would 1																			19
			be located when graphed on a number line?
		b. Between what two whole numbers would 1
		b. Between what two whole numbers would 1																				50
			be located when graphed on a number line?
	NOTATION
	NOTATION
Fill in the blanks.
17.		a.	The symbol 1 is used to indicate a positive
														.	1
		b.	The symbol																is used to indicate the
		b.	The symbol																is used to indicate the
			square root of a positive number.
18.		41				means 4									1

				9													9.
Complete each solution to evaluate the expression.
19.		1					1
19.		1			49		1			64
			1
20.		21						51					2(							) 5(	)
20.		21		100				51				25	2(							) 5(	)
																			25
																			25
			5

GUIDED PRACTICE

Find the two square roots of each number. See Example 1.

21.	25	22.	1
23.	6	24.	44

Evaluate each square root without using a calculator.

See Example 2.
29.					30.
29.		16144			30.		16121
25.	1				26.	164
27.			9		28.
31.					32.

				49				81

Use a calculator to evaluate each square root.
See Objective 1, Using Your Calculator.
	1			1
33.		961	34.		841
35.	3,969		36.	5,625

Evaluate each square root without using a calculator.

See Example 3.

37.	B				4																											38.		B					36
37.	B		25																													38.		B			121

39.	B						16																									40.		B						64

							9																																	25
41.	B						1																									42.		B						1

							81																																	4
43.	10.64																															44.		10.36
45.	1																															46.		1
45.	1						0.81																									46.		1						0.49
47.	10.09																															48.		10.01
Evaluate each expression without using a calculator.
See Example 4.
53.																																54.
53.	81144																116															54.		11 1196
49.	136 11																															50.		1100											1
51.																																52.													136
51.															49																	52.				4									136
55.																																56.														16

							225												144																						169											16
Evaluate each expression without using a calculator.
See Example 5.
61.																			14													62.		6
61.	41169 2																		14													62.		6					8181 51
57.	4	125																														58.		2	1
59.	10						1																									60.		40						1
59.	10						1				196																					60.		40						1					4

63.	8											51																				64.		3														21
63.	8								16			51								225												64.		3											169			21					225
Evaluate each expression without using a calculator.
See Example 6.																								1
65.	15 4 C52 (6 1)																													D
65.	15 4 C52 (6 1)																										4			D
66.	18 2 C42 (7 3)1																														D
66.	18 2 C42 (7 3)1																											9			D
67.	50 C(62 24) 9																							1								D
67.	50 C(62 24) 9																							1	25							D
68.	40 C(72 40) 7																							1									D
68.	40 C(72 40) 7																							1		64							D
69.	1								3						1		52 2					1							2
69.	1			196					3						1		52 2					1	225						2
70.	1								2						1		72 3					1							2
70.	1		169						2						1		72 3					1	144						2
	1							6(22)																																		3(16)
	1					16		6(22)																														49				3(16)
71.							1																									72.		1									1
71.							1				4																					72.		1					16				1						64

			1														9																		25										64
73.	B								B																							74.		B											B
73.	B				16				B							25																74.		B					9						B					81
75.	5	1					1							2	( 2)2																	76.		1					1						2( 2)(3)3
75.	5	1					1			49				2	( 2)2																	76.		1					1					64	2( 2)(3)3
77.	(62)10.04 2.36																															78.		(52)10.25 4.7
	1 31																	52																1 2											1						6			2
79.	1 31												1.44					52														80.		1 2											1		1.21				6			2
Evaluate each formula without using a calculator.
See Example 7.																			2

81.	Evaluate c																				a2 b2												for a 9 and b 12.
82.	Evaluate c																				a2 b2												for a 6 and b 8.

83.Evaluate a 2c2 b2 for c 25 and b 24.

84.Evaluate b c2 a2 for c 17 and a 8.

Use a calculator (or the square root table in Appendix III) to complete each square root table. Round to the nearest thousandth when an answer is not exact. See Example 8.

85.			86.
		Square			Square
	Number	Root		Number	Root

	1			10
	2			20
	3			30
	4			40
	5			50
	6			60
	7			70
	8			80
	9			90
	10			100

Use a calculator (or a square root table) to approximate each of
the following to the nearest hundredth. See Example 8.
	1			1
87.	1	15	88.	1	51
89.	66		90.	204


91.	1			92.	1
		24.05					70.69
93.	1			94.
			11.1			0.145

Use a calculator to approximate each of the following to the nearest thousandth. See Example 8.

APPLICATIONS

In the following problems, some lengths are expressed as square roots. Solve each problem by evaluating any square roots. You may need to use a calculator. If so, round to the nearest tenth when an answer is not exact.

95.CARPENTRY Find the length of the slanted side of each roof truss shown below.

25 ft 3 ft

4 ft

100 ft 6 ft

8 ft

4.6 Square Roots

393

96.RADIO ANTENNAS Refer to the illustration below. How far from the base of the antenna is each guy wire anchored to the ground? (The measurements are in feet.)

Anchor

points

Anchor

point

√144 √16

√36

97.BASEBALL The illustration below shows some dimensions of a major league baseball ﬁeld. How far is it from home plate to second base?

90 ft

√16,200 ft

90 ft

98.SURVEYING Refer to the illustration below. Use the imaginary triangles set up by a surveyor to

ﬁnd the length of each lake. (The measurements are in meters.)

Length: √

318,096

Length: √93,025

394	Chapter 4 Decimals

99.FLATSCREEN TELEVISIONS The picture screen on a television set is measured diagonally. What size screen is shown below?

√1,764 in.

100.LADDERS A painter’s ladder is shown below. How long are the legs of the ladder?

√225 ft

√169 ft

WRITING 1

101. When asked to ﬁnd 16, a student answered 8. Explain his misunderstanding of the concept of square root.

102.Explain the difference between the square and the square root of a number. Give an example1 .

103.What is a nonterminating decimal? Use an example in your explanation1 .

104.a. How would you check whether1 389 1 17? b. How would you check whether 7 2.65?

105.Explain1 why 4 does not represent a real number.

106.Is there a difference between 25 and 25? Explain.

107.6 2.449. Explain why an symbol is used and

not an symbol.

108. Without1 evaluating1 1 the1following1 square roots, determine which is the largest and which is the smallest. Explain how you decided.

23, 27, 11, 6, 20

REVIEW

109.Multiply: 6.75 12.2

110.Divide: 5.7 18.525

111.Evaluate: (3.4)3

112.Add: 23.45 76 0.009 3.8

STUDY SKILLS CHECKLIST

Do You Know the Basics?

The key to mastering the material in Chapter 4 is to know the basics. Put a checkmark in the box if you can answer “yes” to the statement.

I have memorized the place-value chart on page 317.

I know the rules for rounding a decimal to a certain decimal place value by identifying the rounding digit and the test digit.

I know how to add decimals using carrying and how to subtract decimals using borrowing.

1	1		9
	7.18	6	10 14
		537.0 4

		154.20	2 3. 9 8
		46.03
			513. 0 6
		207.41

I have memorized the list of perfect squares on

page 387 and can ﬁnd their square roots.
216 4	2121 11

I know how to multiply and divide decimals and locate the decimal point in the answer.

1.84			2.8
	3.4
			9.5 2
7. 6
	68
1104

12880			272
		272
13.984
			0

I know how to use division to write a fraction as a decimal.

		0.6
3		5
	0.6		3.0
5		30
		0

The place value of the digit 3 is 3 hundredths.

The digit that tells the number of ten-thousandths is 1.

Write 28. 9341 in expanded notation:

9 3 4 1 28.9341 20 8 10 100 1,000 10,000

Write the decimal in words and then as a fraction or mixed number:

28 . 9341 The whole-number part is 28. The fractional part is 9341.

The digit the farthest to the right, 1, is in the tenthousandths place.

Twenty-eight and nine thousand three hundred forty-one

ten-thousandths

9,341 Written as a mixed number, 28.9341 is 28 10,000 .

Write the decimal in words and then as a fraction or mixed number:

0 . 079 The whole-number part is 0. The fractional part is 79. The digit the farthest to the right, 9, is in the thousandths place.

Seventy-nine thousandths

79 Written as a fraction, 0.079 is 1,000 .

Write the decimal number in standard form:

395

C H A P T E R 4 SUMMARY AND REVIEW

S E C T I O N 4.1 An Introduction to Decimals

DEFINITIONS AND CONCEPTS

The place-value system for whole numbers can be extended to create the decimal numeration system.

The place-value columns to the left of the decimal point form the whole-number part of the decimal number. The value of each of those columns is 10 times greater than the column directly to its right.

The columns to the right of the decimal point form the fractional part. Each of those columns has a value that is 101 of the value of the place directly to its left.

To write a decimal number in expanded form (expanded notation) means to write it as an addition of the place values of each of its digits.

To read a decimal:

1.Look to the left of the decimal point and say the name of the whole number.

2.The decimal point is read as “and.”

3.Say the fractional part of the decimal as a whole number followed by the name of the last place-value column of the digit that is the farthest to the right.

We can use the steps for reading a decimal to write it in words.

The procedure for reading a decimal can be applied in reverse to convert from written-word form to standard form.

EXAMPLES

Whole-number part

Fractional part

ths

Tens

Ones

Ten

ths

-thousand-thousand

Thousands

point

ths

Hundred

Hundreds

Decimal

ths

Thousand

ndred

Ten

1,000 100 10

––

–––

––––

–––––

––––––

100

1,000

10,000

100,000

Negative twelve and sixty-ﬁve ten-thousandths

12.0065

This is the ten-thousandths place-value column. Two place holder 0’s must be inserted here so that the last digit in 65 is in the tenthousandths column.

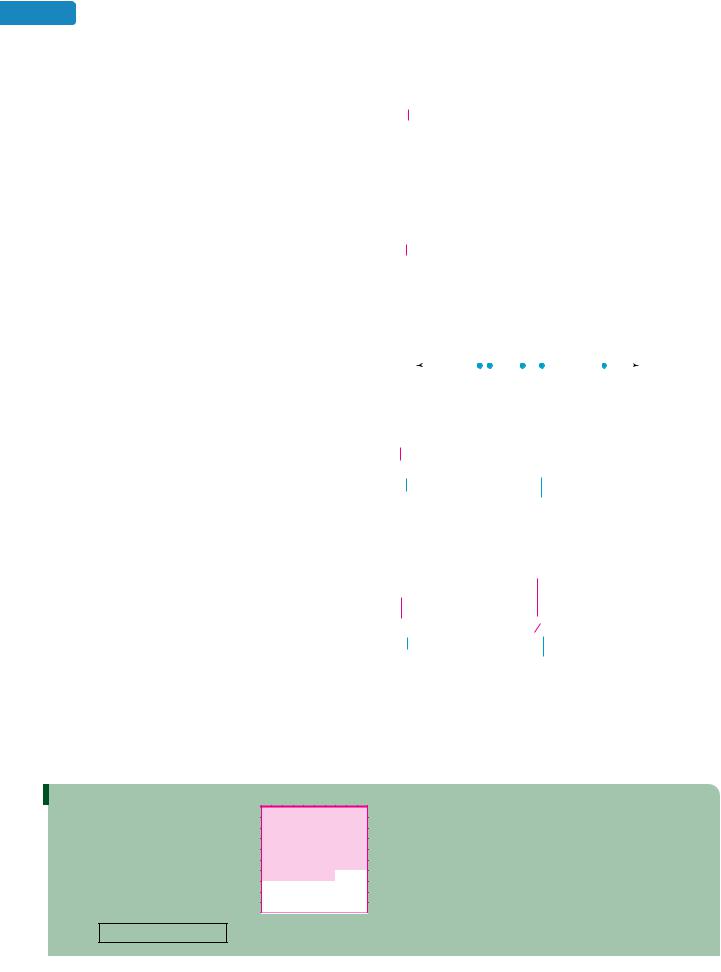
396

Chapter 4

Decimals

To compare two decimals:

Compare 47.31572 and 47.31569.

Make sure

both numbers have the same

47.315

number of decimal places to the right of the

47.315

decimal point. Write any additional zeros

As we work from left to right, this is the ﬁrst column in

necessary to achieve this.

2. Compare the digits of each decimal, column by

which the digits differ. Since 7 6, it follows that

47.31572 is greater than 47.31569.

column, working from left to right.

Thus, 47.31572 47.31569.

3. If the decimals are positive: When two digits

Compare 6.418 and 6.41.

differ, the decimal with the greater digit is the

greater number.

6.41

These decimals are negative.

If the decimals are negative: When two digits

6.41

Write a zero after 1 to help in the comparison.

differ, the decimal with the smaller digit is the

As we work from left to right, this is the ﬁrst column in

greater number.

which the digits differ. Since 0 8, it follows that 6.410

is greater than 6.418.

Thus, 6.41 6.418.

To graph a decimal number means to make a

Graph 2.17, 0.6, 2.89, 3.99, and 0.5 on a number line.

drawing that represents the number.

–2.89 –2.17 –0.5 0.6

3.99

−5 − 4 −3 −2 −1 0 1 2 3 4 5

To round a decimal to a certain decimal place

Round 33.41632 to the nearest thousandth.

value, locate the rounding digit in that place.

Rounding digit:

Keep the rounding digit:

Look at the test digit directly to the right of the

thousandths column

Do not add 1.

rounding digit.

33.41632

If the test digit is 5 or greater, round up by

adding 1 to the rounding digit and dropping all

Test digit: 3 is less than 5.

Drop the test digit and all

the digits to its right. If the test digit is less than

digits to its right.

5, round down by keeping the rounding digit

Thus, 33.41632 rounded to the nearest thousandth is 33.416.

and dropping all the digits to its right.

Round 2.798 to the nearest hundredth.

Rounding digit:

Add 1. Since 9 1 10,

hundredths column

write 0 in this column and

carry 1 to the tenths column.

2.798

Test digit: 8 is 5 or greater.

Drop the test digit.

Thus, 2.798 rounded to the nearest hundredth is 2.80.

There are many situations in our daily lives that

Rounded to the nearest cent, $0.14672 is $0.15.

call for rounding amounts of money.

Rounded to the nearest dollar, $142.39 is $142.

REVIEW EXERCISES

1.a. Represent the amount of the square region that is shaded, using a decimal and a fraction.

b.Shade 0.8 of the region shown below.

2.Consider the decimal number 2,809.6735.

a.What is the place value of the digit 7?

b.Which digit tells the number of thousandths?

c.Which digit tells the number of hundreds?

d.What is the place value of the digit 5?

3.Write 16.4523 in expanded notation.

Write each decimal in words and then as a fraction or mixed number.

4.2.3

5.–615.59

6.0.0601

7.0.00001

Write each number in standard form.

8.One hundred and sixty-one hundredths

9.Eleven and nine hundred ninety-seven thousandths

10.Three hundred one and sixteen millionths

Chapter 4 Summary and Review

397

23.0.2222282 nearest millionth

24.0.635265 nearest hundred-thousandth

Round each given dollar amount.

25.$0.671456 to the nearest cent

26.$12.82 to the nearest dollar

27.VALEDICTORIANS At the end of the school year, the ﬁve students listed below were in the running to be class valedictorian (the student with the highest grade point average). Rank the students in order by GPA, beginning with the valedictorian.

Place an or an symbol in the box to make a true statement.

11.5.68 5.75

12.106.8199 106.82

13.78.23 78.303

14.555.098 555.0991

15.Graph: 1.55, 0.8, 2.1, and 2.7.

–5 –4 –3 –2 –1 0 1 2 3 4 5

16. Determine whether each statement is true or false.

a.	78 78.0	b. 6.910	6.901
c.	3.4700 3.470	d. 0.008	.00800

Round each decimal to the indicated place value.

17.4.578 nearest hundredth

18.3,706.0815 nearest thousandth

19.0.0614 nearest tenth

20.88.12 nearest tenth

21.6.702983 nearest ten-thousandth

22.11.314964 nearest ten-thousandth

Name GPA

Diaz, Cielo	3.9809
Chou, Wendy	3.9808

Washington, Shelly	3.9865

Gerbac, Lance	3.899

Singh, Amani	3.9713

28.ALLERGY FORECAST The graph below shows a four-day forecast of pollen levels for Las Vegas, Nevada. Determine the decimal-number forecast for each day.

Allergy Alert 4-Day Forecast

for Las Vegas, Nevada

4.0
3.0
2.0
1.0
Sun.	Mon.	Tues.	Wed.

S E C T I O N 4.2	Adding and Subtracting Decimals


DEFINITIONS AND CONCEPTS		EXAMPLES
To add or subtract decimals:		Add: 15.82 19 32.995
1. Write the numbers in vertical form with the		Write the problem in vertical form and add, column-by-column,
decimal points lined up.
decimal points lined up.		working right to left.
		working right to left.
2. Add (or subtract) as you would whole numbers.		1 1 1
3. Write the decimal	point in the result from	15.820 Insert an extra zero.
3. Write the decimal	point in the result from	19.000 Insert a decimal point and extra zeros.
Step 2 below the decimal points in the problem.		19.000 Insert a decimal point and extra zeros.
Step 2 below the decimal points in the problem.		32.995
If the number of decimal places in the problem are		32.995
If the number of decimal places in the problem are		67.815
different, insert additional zeros so that the		67.815
different, insert additional zeros so that the			Line up the decimal points.
number of decimal places match.


		To check the result, add bottom to top.

398

Chapter 4

Decimals

If the sum of the digits in any place-value column

Subtract:

8.4 3.029

is greater than 9, we must carry.

Write the problem in vertical form and subtract, column-by-column,

If the subtraction of the digits in any place-value

working right to left.

column requires that we subtract a larger digit

from a smaller digit, we must borrow or regroup.

3 10 10

Insert extra zeros.

8.4 0 0

3.0 2 9

First, borrow from the tenths column: then

5.3 7 1

borrow from the hundredths column.

To check: The sum of the difference and the subtrahend should

equal the minuend.

1 1

5.371

Difference

3.029 Subtrahend

8.400

Minuend

To add signed decimals, we use the same rules that

Add:

21.35 ( 64.52)

are used for adding integers.

Find the absolute values:

0 21.35 0

21.35 and 0 64.52 0 64.52

With

like signs: Add their absolute values and

21.35 ( 64.52) 85.87

Add the absolute values, 21.35

attach their common sign to the sum.

and 64.52, to get 85.87. Since

With unlike signs: Subtract their absolute values

both decimals are negative, make

(the smaller from the larger). If the positive

the ﬁnal result negative.

decimal has the larger absolute value, the ﬁnal

Add:

7.4 9.8

answer is positive. If the negative decimal has the

Find the absolute values: 0

7.4 0 7.4 and

09.8 0 9.8

larger absolute value, make the ﬁnal answer

negative.

7.4 9.8 2.4 Subtract the smaller absolute value from the

larger: 9.8 7.4 2.4. Since the positive

number, 9.8, has the larger absolute value, the

ﬁnal answer is positive.

To subtract two signed decimals, add the ﬁrst

Subtract:

8.62 ( 1.4)

decimal to the

opposite of the decimal to be

The number to be subtracted is 1.4. Subtracting 1.4 is the same

subtracted.

as adding its opposite, 1.4.

Add . . .

8.62 ( 1.4) 8.62 1.4 7.22

Use the rule for

adding two decimals

. . . the opposite

with different signs.

Estimation can be used to check the

Estimate the sum by rounding the addends to the nearest ten:

reasonableness of an answer to a decimal addition

328.99 459.02

or subtraction.

328.99

330 Round to the nearest ten.

459.02

460

Round to the nearest ten.

788.01

790 This is the estimate.

Estimate the difference by using front-end rounding: 302.47 36.9

Each number is rounded to its largest place value.

302.47

300 Round to the nearest hundred.

36.9

Round to the nearest ten.

265.57

260 This is the estimate.

We can use the ﬁve-step problem-solving strategy

See Examples 10–12 that begin on page 337 to review how to solve

to solve application problems that involve decimals.

application problems by adding and subtracting decimals.

REVIEW EXERCISES

Perform each indicated operation.

29.19.5 34.4 12.8

30.3.4 6.78 35 0.008

31.68.47 53.3

32.45.8 17.372

33.9,000.09 7,067.445

34.8.61

5.97

9.72

35.	16.1	8.4	36.	4.8 ( 7.9)
37.	3.55	( 1.25)	38.	15.1 13.99

Evaluate each expression.

39.8.8 ( 7.3 9.5)

40.(5 0.096) ( 0.035)

41.a. Estimate the sum by rounding the addends to the nearest ten: 612.05 145.006

b.Estimate the difference by using front-end rounding: 289.43 21.86

Chapter 4 Summary and Review

399

42.COINS The thicknesses of a penny, nickel, dime, quarter, half-dollar, and presidential $1 coin are

1.55millimeters, 1.95 millimeters, 1.35 millimeters,

1.75millimeters, 2.15 millimeters, and 2.00 millimeters, in that order. Find the height of a stack made from one of each type of coin.

43.SALE PRICES A calculator normally sells for $52.20. If it is being discounted $3.99, what is the sale price?

44.MICROWAVE OVENS A microwave oven is shown below. How tall is the window?

2.5 in.

	2:17
	TIME	CLOCK	AUTO
	1	2	3	13.4 in.
?	1	2	3
?	4	5	6
	7	8	9
	POWER	0	LIGHT
	LEVEL	0	LIGHT

2.75 in.

S E C T I O N 4.3 Multiplying Decimals

DEFINITIONS AND CONCEPTS

To multiply two decimals:

1.Multiply the decimals as if they were whole numbers.

2.Find the total number of decimal places in both factors.

3.Insert a decimal point in the result from step 1 so that the answer has the same number of decimal places as the total found in step 2.

When multiplying decimals, we do not need to line up the decimal points.

Multiplying a decimal by 10, 100, 1,000, and so on

To ﬁnd the product of a decimal and 10, 100, 1,000, and so on, move the decimal point to the right the same number of places as there are zeros in the power of 10.

Multiplying a decimal by 0.1, 0.01, 0.001, and so on

To ﬁnd the product of a decimal and 0.1, 0.01, 0.001, and so on, move the decimal point to the left the same number of places as there are in the power of 10.

EXAMPLES

Multiply: 2.76 4.3

Write the problem in vertical form and multiply 2.76 and 4.3 as if they were whole numbers.

2.76	2 decimal places.		The answer will have
4.3	1 decimal place.	v	The answer will have
4.3	1 decimal place.	v	2 1 3 decimal places.
828
11040
11.868	Move 3 places from right to left and insert
	a decimal point in the answer.
	a decimal point in the answer.
Thus, 2.76 4.3 11.868.
Multiply:
84.561	10,000 845,610		Since 10,000 has four zeros, move the
			decimal point in 84.561 four places to
			decimal point in 84.561 four places to
			the right. Write a placeholder zero
			(shown in blue).
Multiply:
32.67 0.01 0.3267		Since 0.01 has two decimal places, move the

decimal point in 32.67 two places to the left.

Multiply the absolute values, 5.7 and 0.4, to get 2.28.

Make the ﬁnal answer negative.

5.7(0.4) 2.28

400	Chapter 4 Decimals


	The rules for multiplying integers also hold for	Multiply:	( 0.03)( 4.1)
	multiplying signed decimals:	Find the absolute values:		0	0.03 0 0.03 and 04.1 0 4.1
		Find the absolute values:		0	0.03 0 0.03 and 04.1 0 4.1
	The product of two decimals with like signs is	Since the decimals have like signs, the product is positive.
	positive, and the product of two decimals with
	positive, and the product of two decimals with	( 0.03)( 4.1) 0.123			Multiply the absolute values,
	unlike signs is negative.	( 0.03)( 4.1) 0.123			Multiply the absolute values,
					0.03 and 4.1, to get 0.123.
		Multiply:	5.7(0.4)
		Find the absolute values:		0	5.7 0 5.7 and 00.4 0 0.4
		Since the decimals have unlike signs, the product is negative.

We can use the rule for multiplying a decimal by a	Write 4.16 billion in standard notation:
power of ten to write large numbers in standard	4.16 billion 4.16			1 billion
form.	4.16 billion 4.16			1 billion
form.		4.16 1,000,000,000 Write 1 billion in standard form.
		4.16 1,000,000,000 Write 1 billion in standard form.
		4,160,000,000				Since 1,000,000,000 has nine
						zeros, move the decimal point in
						zeros, move the decimal point in
						4.16 nine places to the right.

The base of an exponential expression can be a	Evaluate:	(1.5)2
positive or a negative decimal.	(1.5)2 1.5 1.5			The base is 1.5 and the exponent is 2. Write the base
				as a factor 2 times.
	2.25			Multiply the decimals.
	Evaluate: ( 0.02)2
	( 0.02)2 ( 0.02)( 0.02)					The base is 0.02 and the exponent is 2.
						Write the base as a factor 2 times.
	0.0004					Multiply the decimals. The product of two
						decimals with like signs is positive.

To evaluate a formula, we replace the letters with	Evaluate P 2l 2w for l 4.9 and w 3.4.
speciﬁc numbers and then use the order of	P 2l 2w
operations rule.	P 2l 2w
operations rule.	2(4.9) 2(3.4)				Replace l with 4.9 and w with 3.4.
	2(4.9) 2(3.4)				Replace l with 4.9 and w with 3.4.
	9.8 6.8				Do the multiplication.
	16.6				Do the addition.

Estimation can be used to check the reasonableness	Estimate 37 8.49 by front-end rounding.
of an answer to a decimal multiplication.	37			40 Round to the nearest ten.


	8.49		8		Round to the nearest one.
	8.49		8		Round to the nearest one.

320 This is the estimate.

The estimate is 320. If we calculate 37 8.49, the product is exactly 314.13.

We can use the ﬁve-step problem-solving strategy to See Examples 12 and 13 that begin on page 351 to review how to solve application problems that involve decimals. solve application problems by multiplying decimals.

REVIEW EXERCISES

Multiply.
45.	2.3 6.9	46.	32.45(6.1)
47.	1.7	48.	275
47.	0.004	48.	8.4
49.	15.5( 9.8)	50.	( 0.003)( 0.02)
51.	1,000(90.1452)	52.	0.001(2.897)
Evaluate each expression.
53.	(0.2)2	54.	( 0.15)2

55.(0.6 0.7)2 ( 3)( 4.1)

56.3(7.8) 2(1.1)2

57.( 3.3)2(0.00001)

58.(0.1)3 2 0 45.63 12.24 0

59.Write each number in standard notation.

a.GEOGRAPHY China is the third largest country in land area with territory that extends over 9.6 million square kilometers. (Source: china.org)

b.PLANTING TREES In 2008, the Chinese people planted 2.31 billion trees in mountains, city parks, and along highways to increase the number of forests in their country. (Source: xinhuanet.com)

60.a. Estimate the product using front-end rounding: 193.28 7.63

b.Estimate the product by rounding the factors to the nearest tenth: 12.42 7.38

Chapter 4 Summary and Review

401

61.Evaluate the formula A P Prt for P 70.05, r 0.08, and t 5.

62.SHOPPING If crab meat sells for $12.95 per pound, what would 1.5 pounds of crab meat cost? Round to the nearest cent.

63.AUTO PAINTING A manufacturer uses a threepart process to ﬁnish the exterior of the cars it produces.

Step 1: A 0.03-inch-thick rust-prevention undercoat is applied.

Step 2: Three layers of color coat, each 0.015 inch thick, are sprayed on.

Step 3: The ﬁnish is then buffed down, losing 0.005 inch of its thickness.

What is the resulting thickness of the automobile’s ﬁnish?

64.WORD PROCESSORS The Page Setup screen for a word processor is shown. Find the area that can be ﬁlled with text on an 8.5 in. 11 in. piece of paper if the margins are set as shown.

Page Setup

Margins

Margins Preview

Top	1.0 in.
Bottom	0.6 in.
Left	0.5 in.
Right	0.7 in.
Help	Ok	Cancel

S E C T I O N 4.4 Dividing Decimals

DEFINITIONS AND CONCEPTS

To divide a decimal by a whole number:

1.Write the problem in long division form and place a decimal point in the quotient (answer) directly above the decimal point in the dividend.

2.Divide as if working with whole numbers.

3.If necessary, additional zeros can be written to the right of the last digit of the dividend to continue the division.

EXAMPLES

Divide: 6.2 4

1.55

4 6.20

2 2

2 0

Place a decimal point in the quotient that lines up with the decimal point in the dividend.

Ignore the decimal points and divide as if working with whole numbers.

Write a zero to the right of the 2 and bring it down. Continue to divide.

The remainder is 0.

402		Chapter 4 Decimals

To check the result, we multiply the divisor by the quotient. The result should be the dividend.

To divide with a decimal divisor:

1.Write the problem in long division form.

2.Move the decimal point of the divisor so that it becomes a whole number.

3.Move the decimal point of the dividend the same number of places to the right.

4.Write a decimal point in the quotient (answer) directly above the decimal point in the dividend. Divide as if working with whole numbers.

5.If necessary, additional zeros can be written to the right of the last digit of the dividend to continue the division.

Sometimes when we divide decimals, the subtractions never give a zero remainder, and the division process continues forever. In such cases, we can round the result.

To estimate quotients, we use a method that approximates both the dividend and the divisor so that they divide easily. There is one rule of thumb for this method: If possible, round both numbers up or both numbers down.

Dividing a decimal by 10, 100, 1,000, and so on

To ﬁnd the quotient of a decimal and 10, 100, 1,000, and so on, move the decimal point to the left the same number of places as there are zeros in the power of 10.

Check:

1.55Quotient

4 Divisor

6.20Dividend

The check conﬁrms that 6.2 4 1.55.

	Divide:	1.462
	Divide:	3.4
		3.4
	3.4 1.462 Write the problem in long division form. Move the decimal

point of the divisor, 3.4, one place to the right to make it a whole number. Move the decimal point of the dividend, 1.462, the same number of places to the right.

Now use the rule for dividing a decimal by a whole number.

0.4 3

34 14.6 213 6

1 0 21 0 2 0

Write a decimal point in the quotient (answer) directly above the decimal point in the dividend.

Divide as with whole numbers.

Divide: 0.77 6. Round the quotient to the nearest hundredth.

To round to the hundredths column, we need to continue the division process for one more decimal place, which is the thousandths column.

Rounding digit: hundredths column

Test digit: Since 8 is 5 or greater, add 1

to the rounding digit and drop the test digit.

0.128

0.770

The remainder is still not 0.

Thus, 0.77 6 0.13.

Estimate the quotient: 337.96 23.8

The dividend is

approximately

337.96 23.8

320 20 16 To divide, drop one zero from

320 and one zero from 20,

The divisor is

and then ﬁnd 32 2.

approximately

The estimate is 16. (The exact answer is 14.2.)

Divide: 79.36 10,000

79.36 10,000 0.007936 Since the divisor 10,000 has four zeros, move the decimal point four

places to the left. Insert two placeholder zeros (shown in blue).

403

Dividing a decimal by 0.1, 0.01, 0.001, and so on

Divide:

1.6402

To ﬁnd the quotient of a decimal and 0.1, 0.01,

0.001

0.001, and so on, move the decimal point to the

1.6402

1,640.2

Since the divisor 0.001 has three decimal places,

right the same number of decimal places as there

0.001

move the decimal point in 1.6402 three places to

are in the power of 10.

the right.

The rules for dividing integers also hold for

Divide:

1.53

0.3

5.1 Since the signs of the dividend and divisor

dividing signed decimals. The quotient of two

are unlike, the ﬁnal answer is negative.

decimals with like signs is positive, and the

0.84

quotient of two decimals with unlike signs is

Divide:

0.2

Since the dividend and divisor have like signs,

4.2

negative.

the quotient is positive.

We use the order of operations rule to evaluate

Evaluate:

37.8 (1.2)2

expressions and formulas.

0.1 0.3

37.8 (1.2)2

37.8 1.44 In the numerator, evaluate (1.2)2.

0.1 0.3

0.4

In the denominator, do the addition.

36.36

In the numerator, do the subtraction.

0.4

90.9

Do the division indicated by the fraction

bar.

We can use the ﬁve-step problem-solving strategy to

See Examples 10 and 11 that begin on page 366 to review how to

solve application problems that involve decimals.

solve application problems by dividing decimals.

REVIEW EXERCISES

Divide. Check the result.
65.		66.	41.8 4
65.	3 27.9	66.	41.8 4
67.	29.67	68.	24.618 0.6
67.	23	68.	24.618 0.6
	23
69.	80.625 12.9	70.	0.0742

			1.4
			1.4
71.	15.75	72.	0.003726

	0.25		0.0046
73.	89.76 1,000	74.	0.0112
73.	89.76 1,000	74.	10
			10

75.Divide 0.8765 by 0.001.

76.77.021 0.0001

Estimate each quotient:

77.4,983.01 41.33

78.8.8 25,904.39

Divide and round each result to the speciﬁed decimal place.

79.78.98 6.1 (nearest tenth)

80.5.438 (nearest hundredth) 0.007

(1.4)2 2( 4.6)

81.Evaluate:

0.50.3

82.Evaluate the formula C 59 (F 32) for F 68.9.

83.THANKSGIVING DINNER The cost of purchasing the food for a Thanksgiving dinner for a family of 5 was $41.70. What was the cost of the dinner per person?

84.DRINKING WATER Water samples from ﬁve wells were taken and tested for PCBs (polychlorinated biphenyls). The number of parts per billion (ppb) found in each sample is given below. Find the average number of parts per billion for these samples.

Sample #1: 0.44 ppb

Sample #2: 0.50 ppb

Sample #3: 0.46 ppb

Sample #4: 0.52 ppb

Sample #5: 0.63 ppb

85.SERVING SIZE The illustration below shows the package labeling on a box of children’s cereal. Use the information given to ﬁnd the number of servings.

Nutrition Facts

Serving size	1.1 ounce
Servings per container	?
Package weight	15.4 ounces

Write a decimal point and one additional zero to the right of 3.

404	Chapter 4 Decimals

86.TELESCOPES To change the position of a focusing mirror on a telescope, an adjustment knob is used. The mirror moves 0.025 inch with each revolution of the knob. The mirror needs to be

moved 0.2375 inch to improve the sharpness of the image. How many revolutions of the adjustment knob does this require?

S E C T I O N 4.5 Fractions and Decimals

DEFINITIONS AND CONCEPTS

A fraction and a decimal are said to be equivalent if they name the same number.

To write a fraction as a decimal, divide the numerator of the fraction by its denominator.

Sometimes, when ﬁnding the decimal equivalent of a fraction, the division process ends because a remainder of 0 is obtained. We call the resulting decimal a terminating decimal.

If the denominator of a fraction in simpliﬁed form has factors of only 2’s or 5’s, or a combination of both, it can be written as a decimal by multiplying it by a form of 1. The objective is to write the fraction in an equivalent form with a denominator that is a power of 10, such as 10, 100, 1,000, and so on.

Sometimes, when we are ﬁnding the decimal equivalent of a fraction, the division process never gives a remainder of 0. We call the resulting decimal a repeating decimal.

An overbar can be used instead of the three dots

. . . to represent the repeating pattern in a repeating decimal.

When a fraction is written in decimal form, the result is either a terminating or repeating decimal. Repeating decimals are often rounded to a speciﬁed place value.

EXAMPLES

Write 35 as a decimal.

We divide the numerator by the denominator because a fraction bar indicates division: 35 means 3 5.

0.6

5 3.0


30
		0	Since a zero remainder is obtained, the
		0	Since a zero remainder is obtained, the
			result is a terminating decimal.
Thus,	3	0.6. We say that 0.6 is the decimal equivalent of		3.
	5			5
Write	3	as a decimal.
Write	25	as a decimal.
	25

Since we need to multiply the denominator of												3	by 4 to obtain a
Since we need to multiply the denominator of												25	by 4 to obtain a
denominator of 100, it follows that 4 should be												25
denominator of 100, it follows that 4 should be
						4
the form of 1 that is used to build									3	.
the form of 1 that is used to build										.
						25
	3			3	4	Multiply	3	by 1 in the form of			4.
25					4	Multiply		by 1 in the form of			4.
25			25		4	25					4
				12		Multiply the numerators.
						Multiply the denominators.
			100			Multiply the denominators.
			0.12			Write the fraction as a decimal.
Write			5 as a decimal.
			6
0.833
6
6		5.000			Write a decimal point and three
4 8					additional zeros to the right of 5.

			20
18					It is apparent that 2 will continue to reappear as the
					It is apparent that 2 will continue to reappear as the

			20		remainder. Therefore, 3 will continue to reappear in the
			18		remainder. Therefore, 3 will continue to reappear in the
			18		quotient. Since the repeating pattern is now clear, we can
			2		quotient. Since the repeating pattern is now clear, we can
			2		stop the division.

Thus, 56 0.8333 . . . , or, using an overbar, we have 56 0.83.

The decimal equivalent for 115 is 0.454545 . . . . Round it to the nearest hundredth.

					Rounding digit: hundredths column.
					Rounding digit: hundredths column.
5					Test digit: Since 4 is less than 5, round down.
					Test digit: Since 4 is less than 5, round down.


			0.454545 . . .
	11		0.454545 . . .
Thus,		5		0.45.
Thus,		11		0.45.

Chapter 4 Summary and Review	405

To write a mixed number in decimal form, we need only ﬁnd the decimal equivalent for the fractional part of the mixed number.The whole-number part in the decimal form is the same as the wholenumber part in the mixed-number form.

A number line can be used to show the relationship between fractions and decimals.

To compare the size of a fraction and a decimal, it is helpful to write the fraction in its equivalent decimal form.

To evaluate expressions that can contain both fractions and decimals, we can work in terms of decimals or in terms of fractions.

We can use the ﬁve-step problem-solving strategy to solve application problems that involve fractions and decimals.

Whole-number part

4 7		4.875

	b
8

Write the fraction as a decimal.

Graph 3.125, 457, 0.6, 1.09 on a number line.

	5
–4	–
–4	–	–1.09	0.6	3.125
	7	–1.09	0.6	3.125

−5 − 4 −3 −2 −1 0 1 2 3 4 5

Place an , , or an symbol in the box to make a true statement:

0.07

To write 503 as a decimal, divide 50 by 3: 503 0.06.

Since 0.06 is less than 0.07, we have: 503 0.07.

Evaluate:			1	0.31
			6
If we work in terms of fractions, we have:
	1	0.31			1				31					Write 0.31 in fraction form.
	6	0.31			6			100						Write 0.31 in fraction form.
					1	50				31			3	The LCD is 300. Build each fraction
														by multiplying by a form of 1.
					6		50					100	3	by multiplying by a form of 1.
					50						93			Multiply the numerators.
					300					300				Multiply the denominators.
					143									Add the numerators and write the
					300									sum over the common denominator
														300.

If we work in terms of decimals, we have:

See Example 13 on page 381 to review how to solve application problems involving fractions and decimals.

REVIEW EXERCISES

Write each fraction or mixed number as a decimal. Use an							Write each fraction as a decimal. Round to the nearest
overbar when necessary.							hundredth.
87.	7		88.	2			95.	19				96.	31

	8				5			33					30
89.	9		90.	3			Place an , , or an symbol in the box to make a true
89.	16		90.	50			statement.
	6					4		13					4
91.			92.				97.			0.499		98.			0.26
	11					3
								25						15
								25						15
	7			26			99.	Write the numbers in order from smallest to largest:
93.	3		94.					3310 ,
93.	3	125	94.	45					0.3,		0.3
									0.3,		0.3

Ask: What positive number, when squared, is 4? The answer is 2 because 22 = 4.

Ask: What positive number, when squared, is 64? The answer is 8 because 82 64.

Ask: What positive number, when squared, is 225? The answer is 15 because 152 225.

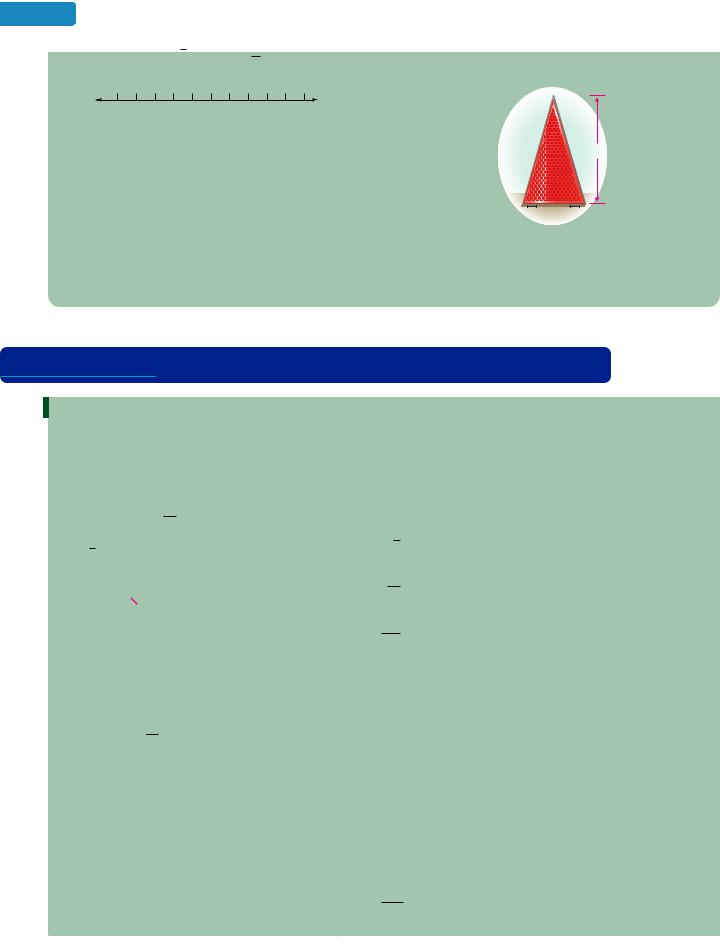
406	Chapter 4 Decimals

100. Graph 1.125, 3.3, 234 , and 109 on a number line.

−5 −4 −3 −2 −1 0 1 2 3 4 5

Evaluate each expression. Work in terms of fractions.

1		0.4	5		0.19
101.			102.
	3			6

Evaluate each expression. Work in terms of decimals.


103.	4	( 7.8)	104.	1	a7.3	5	9	b
	5			8			10
105.	1	(9.7 8.9)(10)	106.	7.5		(0.78)a			1	b	2
	2								2

107.ROADSIDE EMERGENCY What is the area of the reﬂector shown below?

10.9 in.

6.4 in.

108.SEAFOOD A shopper purchased 34 pound of crab meat, priced at $13.80 per pound, and 13 pound of lobster meat, selling for $35.70 per pound. Find the

total cost of these items.

S E C T I O N 4.6 Square Roots

DEFINITIONS AND CONCEPTS

The square root of a given number is a number whose square is the given number.

Every positive number1 has two square roots. The number 0 has only one square root.

as 14, ﬁnd the positive square root of the radicand.

A radical symbol is used to indicate a positive

square root. To evaluate a radical expression such

Radical symbol


	14	Radicand Read as “the


b

Radical expression	square root of 4.”

Numbers such as 4, 64, and 225, that are squares of whole numbers, are called perfect squares. To evaluate square1root radical expressions, it is helpful to be able to identify perfect square radicands.

Review the list of perfect squares on page 00.

The symbol is used to indicate the negative square root of a positive number. It is the opposite of the positive square root.

We can ﬁnd the square root of fractions and decimals.

EXAMPLES

Find the two square roots of 81.

9 is a square root of 81 because 92 81 and

91is a square root of 81 because ( 9)2 81.

Evaluate each square root:

1 4 2

1 64 8

225 15

Evaluate:				1
Evaluate:				1	36
1		is the opposite (or negative) of the square root of 36. Since
1	36
136 6, we have:
1				6
1			36	6
Evaluate each square root:
1
1		49		Ask: What positive fraction, when squared, is								49	?
		49
	B100
												100
				The answer is		7	because 1	7	22	49	.
				The answer is		10	because 1	10	22	100	.

0.25Ask: What positive decimal, when squared, is 0.25? The answer is 0.5 because (0.5)2 0.25.

Chapter 4

Summary and Review

407

When evaluating an expression containing square

20 6123 41

Evaluate:

roots, evaluate square roots at the same stage in

Perform the operations within the parentheses ﬁrst.

your solution as exponential expressions.

20 6123 41

2 20 6(8 4 3)

Within the parentheses,

evaluate the exponential

expression and the square

root.

20 6(8 12)

Within the parentheses, do

the multiplication.

20 6( 4)

Within the parentheses, do

the subtraction.

20 ( 24)

Do the multiplication.

Do the addition.

Evaluate a 2

To evaluate formulas that involve square roots, we

c2 b2

for c 25 and b 20.

replace the letters with speciﬁc numbers and then

a 2c2 b2

This is the formula to evaluate.

use the order of operations rule.

252 202

Replace c with 25 and b with 20.

Evaluate the exponential expressions.

625 400

225

Do the subtraction.

Evaluate the square root.

If a number is not a perfect square, we can use the

Approximate 1

Round to the nearest hundredth.

149.

square root key

on a calculator (or a table of

From a scientiﬁc calculator we get 1

12.20655562. Rounded

149

square roots) to ﬁnd its approximate square root.

to the nearest hundredth,

12.21

149

REVIEW EXERCISES


109.	Find the two square roots of 25.
110.	Fill in the blanks: 1								because						2 49.
110.	Fill in the blanks: 1					49			because						2 49.
Evaluate each square root without using a calculator.
111.	1				112.				1
111.	1	49			112.				1		16
113.	1				114.				1
113.	1	100			114.				1	0.09

	64
115.	B				116.				10.81
115.	B		169		116.				10.81
									10
	1
117.	B				1		8.
117.	B			36	1		8.
119.	Graph each square root:						1	9, 1					1	3, 1
119.	Graph each square root:						1	9, 1				2,	1	3, 1		16

(Hint: Use a calculator or square root table to approximate any square roots, when necessary.)

−5 −4 −3 −2 −1 0 1 2 3 4 5

120. Use a calculator to approximate each square root

to the nearest hundredth.			c. 112.75
a.	119	b. 1598

Evaluate each expression without using a calculator.
121.	31			122.					51
		100										196
										100
123.	3149 136			124.					B				1225
											9
125.	40 6[52 (7 2)			1				D
						16
126.	1 7[62 (1 2)1						D
					81
	Evaluate b 2							for c 17 and a 15.
127.			c2 a2
128.	SHEET METAL Find the length of the side of the
	range hood shown in the illustration below.

129.Between1 what two whole numbers would 183 be located when graphed on a number line?

130.7 2.646. Explain why an symbol is used and not an symbol.1,089 in.

408

C H A P T E R 4 TEST

1.Fill in the blanks.

a.Copy the following addition. Label each addend and the sum.

2.67

6.01

8.68

b.Copy the following subtraction. Label the minuend, the subtrahend, and the difference.

9.6
6.2


3.4

5.Write four thousand ﬁve hundred nineteen and twentyseven ten-thousandths in standard form.

6.Write each decimal in

•expanded form

•words

•as a fraction or mixed number. (You do not have to simplify the fraction.)

a.SKATEBOARDING Gary Hardwick of Carlsbad, California, set the skateboard speed record of 62.55 mph in 1998. (Source: skateboardballbearings.com)

c.Copy the following multiplication. Label the factors and the product.

b. MONEY A dime weighs 0.08013 ounce.

	1.3				7.	Round each decimal number to the indicated
	1.3					place value.
		7				place value.
		7					461.728, nearest tenth
	9.1					a.	461.728, nearest tenth
	9.1
d. Copy the following division. Label the dividend,						b.	2,733.0495, nearest thousandth
d. Copy the following division. Label the dividend,						c. 1.9833732, nearest millionth
	the divisor, and the quotient.					c. 1.9833732, nearest millionth
	the divisor, and the quotient.
			3.4		8. Round $0.648209 to the nearest cent.


			2 6.8		Perform each operation.
e. 0.6666 . . . and 0.8333 . . . are examples of					9.	4.56 2 0.896 3.3
e. 0.6666 . . . and 0.8333 . . . are examples of						Subtract 39.079 from 45.2
	decimals.				10.	Subtract 39.079 from 45.2
f.	The 1		symbol is called a	symbol.	11.	(0.32)2		12.	0.1368
f.	The 1		symbol is called a	symbol.	11.	(0.32)2		12.	0.24
2. Express the amount of the square									0.24
2. Express the amount of the square					13.	6.7( 2.1)		14.	8.7
region that is shaded using a					13.	6.7( 2.1)		14.	8.7
region that is shaded using a									0.004
fraction and a decimal.									0.004
fraction and a decimal.
					15.	11 13		16.	2.4 ( 1.6)
					17. Divide. Round the quotient to the nearest hundredth:
							12.146

3.Consider the decimal number: 629.471

a.What is the place value of the digit 1?

b.Which digit tells the number of tenths?

c.Which digit tells the number of hundreds?

d.What is the place value of the digit 2?

4. WATER PURITY		Pollution,
A county health	City	parts per million
department
department	Monroe	0.0909
sampled the	Monroe	0.0909
sampled the	Covington	0.0899
pollution content of	Covington	0.0899
tap water in ﬁve	Paston	0.0901
cities, with the	Cadia	0.0890
	Cadia	0.0890
results shown. Rank	Selway	0.1001
the cities in order,	Selway	0.1001
the cities in order,
from dirtiest tap water to cleanest.

5.3

18.a. Estimate the product using front-end rounding: 34 6.83

b.Estimate the quotient: 3,907.2 19.3

19.Perform each operation in your head.

a.567.909 1,000

b.0.00458 100

20.Write 61.4 billion in standard notation.

21.EARTHQUAKE DAMAGE After an earthquake, geologists found that the ground on the west side of the fault line had dropped 0.834 inch. The next week,

astrong aftershock caused the same area to sink 0.192 inch deeper. How far did the ground on the west side of the fault drop because of the earthquake and the aftershock?

								Chapter 4	Test	409
22.	NEW YORK CITY Refer to	Central Park North		31.	8 2124 60 61812
	the illustration on the right.				2
	Central Park, which lies in the				2
	Central Park, which lies in the			32.	3 0.7 (Work in terms of fractions.)
	middle of Manhattan, is the			32.	3 0.7 (Work in terms of fractions.)
	middle of Manhattan, is the
	city’s best-known park. If it is	West		33.	a.	Graph 83 , 32 , and 54 on a number line. Label each
	2.5 miles long and 0.5 mile	West				point using the decimal equivalent of the fraction.
	wide, what is its area?	Park
		Park
23.	TELEPHONE BOOKS	Central				−1	0	1
	To print a telephone book,		Ave.		b.	Graph 116, 12,	19, and 15 on a number
	565 sheets of paper were used.		Fifth			line. (Hint: When necessary, use a calculator or
	565 sheets of paper were used.
	If the book is 2.26 inches thick,
	If the book is 2.26 inches thick,					square root table to approximate a square root.)
	what is the thickness of each					square root table to approximate a square root.)
	what is the thickness of each
	sheet of paper?	Central Park South
		Central Park South				−5 − 4 −3 −2 −1 0 1 2 3 4 5
						−5 − 4 −3 −2 −1 0 1 2 3 4 5

24.ACCOUNTING At an ice-skating complex, receipts on Friday were $130.25 for indoor skating and $162.25 for outdoor skating. On Saturday, the corresponding amounts were $140.50 and $175.75. On which day, Friday or Saturday, were the receipts higher? How much higher?

25.CHEMISTRY In a lab experiment, a chemist mixed three compounds together to form a mixture weighing 4.37 g. Later, she discovered that she had forgotten to record the weight of compound C in her notes. Find the weight of compound C used in the experiment.

	Weight

Compound A	1.86 g
Compound B	2.09 g
Compound C	?
Mixture total	4.37 g

26.WEIGHT OF WATER One gallon of water weighs 8.33 pounds. How much does the water in a 212-gallon jug weigh?

27.Evaluate the formula C 2pr for p 3.14 and r 1.7.

28.Write each fraction as a decimal.

17		5
a.		b.
	50		12

Evaluate each expression.

29.4.1 (3.2)(0.4)2

30.a25b2 6 ` 6.2 3 14 `

34. SALADS A shopper purchased 34 pound of potato

salad, priced at $5.60 per pound, and 1 pound of

coleslaw, selling for $4.35 per pound. Find the total cost of these items.

2 3

35. Use a calculator to evaluate c a2 b2 for a 12 and b 35.

a.1 b. 2 169

37.Fill in the blank: 144 because 2 144.

38.Place an , , or an symbol in the box to make a true statement.

a.6.78 6.7936. Write each number in decimal form.2725

	b.		0.3					3
								3
								8
								8

			B		16
	c.				16						0.4

					81
					81
			0.45
	d.		0.45							0.45
Evaluate each expression without using a calculator.
39.	2		1				3				1
39.	2		1	25			3				1	49

			1					1
40.	B				B
40.	B	36			B				25
41.	Evaluate each square root without using a calculator.
	a.		1
	a.		1			0.04
	b.		1
	b.		1		.69
	c.		1225
	d.		1
	d.		1			121
42.	Although the decimal 3.2999 contains more digits
	than 3.3, it is smaller than 3.3. Explain why this is so.

<<< < Предыдущая 23 24 25 26 27 28 29 30 31 32 33 3435 / 6735 36 37 38 39 40 41 42 43 44 45 46 47 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.12.2018408.58 Кб6antikrizisnoe-upravlenie.doc
#
18.12.2018108.03 Кб6ARHITYeKTURA.doc
#
10.06.20158.32 Mб304aswath_damodaran-investment_philosophies_2012.pdf
#
10.06.201582.94 Кб10audit_risk.doc
#
10.06.20154.17 Mб7BallotingApplicationDocs-SIMSUsersGuide.pdf
#
10.06.201515.55 Mб149basic mathematics for college students.pdf
#
10.06.2015901.06 Кб41Bazy_dannykh_i_znanii_UP_SHirokov_L.A._2000.pdf
#
29.03.20162.45 Mб37Bernd_Fon_Vittenburg_-_Shakh_planete_Zemlya.pdf
#
10.06.201561.93 Кб46bezopasnost.docx
#
10.06.20152.89 Mб94bibliofond_ru_604241.docx
#
10.06.20152.1 Mб34blind_watchmaker.pdf