Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный индустриальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

basic mathematics for college students.pdf

Скачиваний:

147

Добавлен:

10.06.2015

Размер:

15.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 6712 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

132 Chapter 2 The Integers

Objectives

S E C T I O N 2.1

1Deﬁne the set of integers.

2Graph integers on a number line.

3Use inequality symbols to compare integers.

4Find the absolute value of an integer.

An Introduction to the Integers

We have seen that whole numbers can be used to describe many situations that arise in everyday life. However, we cannot use whole numbers to express temperatures below zero, the balance in a checking account that is overdrawn, or how far an object is below sea level. In this section, we will see how negative numbers can be used to describe these three situations as well as many others.

5 Find the opposite of an integer.

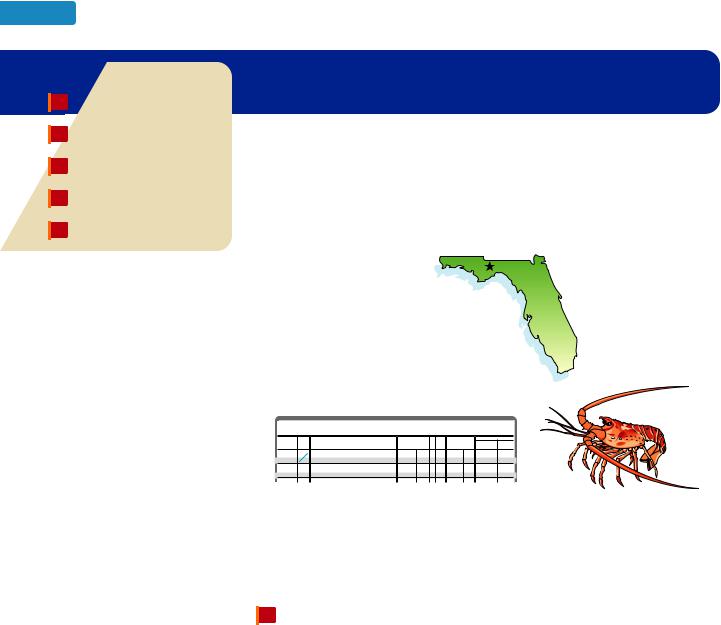
Tallahassee

The record cold temperature in the state of Florida was 2 degrees below zero on February 13, 1899, in Tallahassee.

RECORD ALL CHARGES OR CREDITS THAT AFFECT YOUR ACCOUNT

					FE E			BALANCE
NUMBER	DATE	DESCRIPTION OF TRANSACTION	PAYMENT/DEBIT	√ (IF ANY)		DEPOSIT/CREDIT	$	450 00
NUMBER	DATE	DESCRIPTION OF TRANSACTION	(–)	√ (IF ANY)		(+)	$
1207	5	Wood's Auto Repair	$ 500 00	T	(+)
1207	5	Wood's Auto Repair	$ 500 00		$	$
	2	Transmission

A check for $500 was written	The American lobster is found off
when there was only $450 in the	the East Coast of North America at
account. The checking account	depths as much as 600 feet below
is overdrawn.	sea level.

1 Deﬁne the set of integers.

To describe a temperature of 2 degrees above zero, a balance of $50, or 600 feet above sea level, we can use numbers called positive numbers. All positive numbers are greater than 0, and we can write them with or without a positive sign .

In words	In symbols	Read as
2 degrees above zero	2 or 2	positive two
A balance of $50	50 or 50	positive ﬁfty
600 feet above sea level	600 or 600	positive six hundred

To describe a temperature of 2 degrees below zero, $50 overdrawn, or 600 feet below sea level, we need to use negative numbers. Negative numbers are numbers less than 0, and they are written using a negative sign .

In words	In symbols	Read as
2 degrees below zero	2	negative two
$50 overdrawn	50	negative ﬁfty
600 feet below sea level	600	negative six hundred

Together, positive and negative numbers are called signed numbers.

2.1 An Introduction to the Integers

133

Positive and Negative Numbers

Positive numbers are greater than 0. Negative numbers are less than 0.

Caution! Zero is neither positive nor negative.

The collection of positive whole numbers, the negatives of the whole numbers, and 0 is called the set of integers (read as “in-ti-jers”).

The Set of Integers

{ . . . , 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, . . . }

The three dots on the right indicate that the list continues forever—there is no largest integer. The three dots on the left indicate that the list continues forever— there is no smallest integer. The set of positive integers is {1, 2, 3, 4, 5, . . . } and the set of negative integers is { . . . , 5, 4, 3, 2, 1}.

The Language of Mathematics Since every whole number is an integer, we say that the set of whole numbers is a subset of the integers.

The set of integers

{ . . . , 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, . . . }

The set of whole numbers

2 Graph integers on a number line.

In Section 1.1, we introduced the number line. We can use an extension of the number line to learn about negative numbers.

Negative numbers can be represented on a number line by extending the line to the left and drawing an arrowhead. Beginning at the origin (the 0 point), we move to the left, marking equally spaced points as shown below.As we move to the right on the number line, the values of the numbers increase. As we move to the left, the values of the numbers decrease.

Numbers get larger

Negative numbers

Zero

Positive numbers

−5

−4

−3

−2

−1

Numbers get smaller

The thermometer shown on the next page is an example of a vertical number line. It is scaled in degrees and shows a temperature of 10°. The time line is an example of a horizontal number line. It is scaled in units of 500 years.

134	Chapter 2 The Integers

0 −10 −20

A vertical number line

MAYA CIVILIZATION

500 B.C.	A.D. 300–
500 B.C.	A.D. 900	A.D. 900–
Maya culture	A.D. 900	A.D. 900–	A.D. 1441
Maya culture	Classic period	A.D. 1400	A.D. 1441
begins	Classic period	A.D. 1400	Mayapán	A.D. 1697
begins	of Maya	Maya culture
	of Maya	Maya culture
	culture	declines	falls to	Last Maya
	culture	declines	invaders	Last Maya
			invaders	city conquered
				by the Spanish

500 B.C. B.C./A.D.

A.D. 500

A.D. 1000

A.D. 1500

A.D. 2000

Based on data from People in Time and Place, Western

Hemisphere (Silver Burdett & Ginn., 1991), p. 129

A horizontal number line

Self Check 1

Graph 4, 2, 1, and 3 on a number line.

−4 −3 −2 −1 0 1 2 3 4

Now Try Problem 23

EXAMPLE 1 Graph 3, 2, 1, and 4 on a number line.

−4 −3 −2 −1 0 1 2 3 4

Strategy We will locate the position of each integer on the number line and draw a bold dot.

WHY To graph a number means to make a drawing that represents the number.

Solution

The position of each negative integer is to the left of 0.The position of each positive integer is to the right of 0.

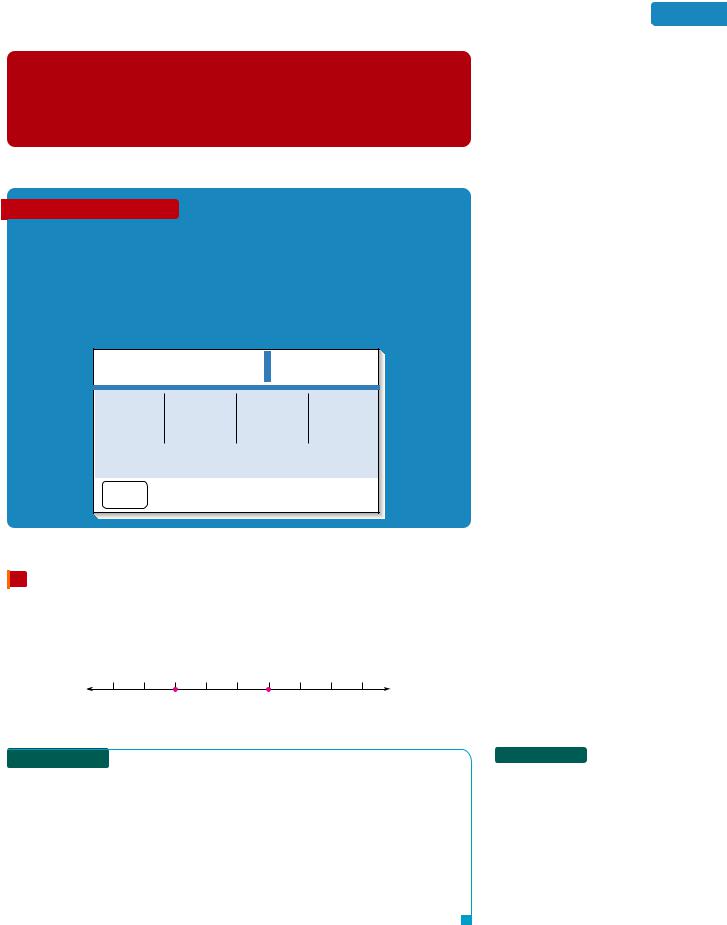
By extending the number line to include negative numbers, we can represent more situations using bar graphs and line graphs. For example, the following bar graph shows the net income of the Eastman Kodak Company for the years 2000 through 2007. Since the net income in 2004 was positive $556 million, the company made a proﬁt. Since the net income in 2005 was $1,362 million, the company had a loss.

Eastman Kodak Company Net Income

	2,000
	1,600	1,407
		1,407
	1,200
	800			770				676
	800					556


millions	400				265
			76		265		'05	'06
			76				'05	'06
	0							Year
		'00	'01	'02	'03	'04		'07
$	–400
	–400
	–800							–601
	–800
	–1,200
	–1,600						–1,362
	–1,600
	–2,000

Source: Morningstar.com

2.1 An Introduction to the Integers

135

The Language of Mathematics Net refers to what remains after all the deductions (losses) have been accounted for. Net income is a term used in business that often is referred to as the bottom line. Net income indicates what a company has earned (or lost) in a given period of time (usually

1 year).

THINK IT THROUGH Credit Card Debt

“The most dangerous pitfall for many college students is the overuse of credit cards. Many banks do their best to entice new card holders with low or zero-interest cards.”

Gary Schatsky, certiﬁed ﬁnancial planner

Which numbers on the credit card statement below are actually debts and, therefore, could be represented using negative numbers?

Account Summary

Previous	New Purchases Payments &	New Balance
Balance	Credits

$4,621		$1,073		$2,369	$3,325

04/21/10			05/16/10		$67
04/21/10			05/16/10		$67
Billing Date			Date Payment Due		Minimum payment

		Periodic rates may vary.
		Periodic rates may vary.
	BANK STAR	See reverse for explanation and important information.
		Please allow sufficient time for mail to reach Bank Star.

3 Use inequality symbols to compare integers.

Recall that the symbol means “is less than” and that means “is greater than.”The ﬁgure below shows the graph of the integers 2 and 1. Since 2 is to the left of 1 on the number line, 2 1. Since 2 1, it is also true that 1 2.

−4 −3 −2 −1 0 1 2 3 4

	EXAMPLE 2	Place an or an symbol in the box to make a true
statement. a. 4			5 b. 8	7

Strategy To pick the correct inequality symbol to place between the pair of numbers, we will determine the position of each number on the number line.

WHY For any two numbers on a number line, the number to the left is the smaller number and the number on the right is the larger number.

Solution

a.Since 4 is to the right of 5 on the number line, 4 5.

b.Since 8 is to the left of 7 on the number line, 8 7.

Self Check 2

Place an or an symbol in the box to make a true statement.

a.6 6

b.11 10

Now Try Problems 31 and 35

136	Chapter 2 The Integers

Self Check 3

Tell whether each statement is true or false.

a.17 15

b.35 35

c.2 2

d.61 62

Now Try Problems 41 and 45

The Language of Mathematics Because the symbol requires one number to be strictly less than another number and the symbol requires one number to be strictly greater than another number, mathematical statements involving the symbols and are called strict inequalities.

There are three other commonly used inequality symbols.

Inequality Symbols

means is not equal to

means is greater than or equal to

means is less than or equal to

5 2 Read as “ 5 is not equal to 2.”

6 10 Read as “ 6 is less than or equal to 10.” This statement is true, because 6 10.

12 12 Read as “12 is less than or equal to 12.” This statement is true, because 12 12.

15 17

20 20

EXAMPLE 3

Read as “ 15 is greater than or equal to 17.” This statement is true, because 15 17.

Read as “ 20 is greater than or equal to 20.” This statement is true, because 20 20.

Tell whether each statement is true or false.

a. 9 9 b. 1 5 c. 27 6 d. 32 32

Strategy We will determine if either the strict inequality or the equality that the symbols and allow is true.

WHY If either is true, then the given statement is true.

Solution

a.9 9 This statement is true, because 9 9.

b.1 5 This statement is false, because neither 1 5 nor 1 5 is true.

c.27 6 This statement is false, because neither 27 6 nor 27 6 is true.

d. 32 31 This statement is true, because 32 31.

4 Find the absolute value of an integer.

Using a number line, we can see that the numbers 3 and 3 are both a distance of 3 units away from 0, as shown below.

			3 units				3 units



−5	−4	−3	−2	−1	0	1		2	3	4	5

The absolute value of a number gives the distance between the number and 0 on the number line. To indicate absolute value, the number is inserted between two vertical bars, called the absolute value symbol. For example, we can write 0 3 0 3. This is read as “The absolute value of negative 3 is 3,” and it tells us that the distance between 3 and 0 on the number line is 3 units. From the ﬁgure, we also see that 0 3 0 3.

2.1 An Introduction to the Integers

137

Absolute Value

The absolute value of a number is the distance on the number line between the number and 0.

Caution! Absolute value expresses distance. The absolute value of a number is always positive or 0. It is never negative.

EXAMPLE 4	Find each absolute value: a. 0 8	0 b. 0 5	0 c. 0 0 0

Strategy We need to determine the distance that the number within the vertical absolute value bars is from 0 on a number line.

WHY The absolute value of a number is the distance between 0 and the number on a number line.

Self Check 4

Find each absolute value:

a.0 9 0

b.0 4 0

Now Try Problems 47 and 49

Solution

a. On the number line, the distance between 8 and 0 is 8. Therefore,

0 8 0 8

b. On the number line, the distance between 5 and 0 is 5. Therefore,

0 5 0 5

c. On the number line, the distance between 0 and 0 is 0. Therefore,

0 0 0 0

5 Find the opposite of an integer.

Opposites or Negatives

Two numbers that are the same distance from 0 on the number line, but on opposite sides of it, are called opposites or negatives.

The ﬁgure below shows that for each whole number on the number line, there is a corresponding whole number, called its opposite, to the left of 0. For example, we see that 3 and 3 are opposites, as are 5 and 5. Note that 0 is its own opposite.

–5	–4	–3	–2	–1	0	1	2	3	4	5

Opposites

To write the opposite of a number, a symbol is used. For example, the opposite of 5 is 5 (read as “negative 5”). Parentheses are needed to express the opposite of a negative number.The opposite of 5 is written as ( 5). Since 5 and 5 are the same distance from 0, the opposite of 5 is 5. Therefore, ( 5) 5. This illustrates the following rule.

The Opposite of the Opposite Rule

The opposite of the opposite (or negative) of a number is that number.

138	Chapter 2 The Integers

Self Check 5

Simplify each expression:

a.( 1)

b.0 4 0

c.0 99 0

Now Try Problems 55, 65, and 67

Number	Opposite
57	57	Read as “negative ﬁfty-seven.”
8	( 8) 8	Read as “the opposite of negative eight is eight.”
0	0 0	Read as “the opposite of 0 is 0.”

The concept of opposite can also be applied to an absolute value. For example, the opposite of the absolute value of 8 can be written as 0 8 0 . Think of this as a twostep process, where the absolute value symbol serves as a grouping symbol. Find the absolute value ﬁrst, and then attach a sign to that result.

First, ﬁnd the absolute value.


0 8 0	8 Read as “the opposite of the absolute value
		of negative eight is negative eight.”

Then attach a sign.

EXAMPLE 5	Simplify each expression: a. ( 44) b. 0 11	0 c. 0 225 0

Strategy We will ﬁnd the opposite of each number.

WHY In each case, the symbol written outside the grouping symbols means “the opposite of.”

Solution

a.( 44) means the opposite of 44. Since the opposite of 44 is 44, we write

( 44) 44

b.0 11 0 means the opposite of the absolute value of 11. Since 0 11 0 11, and the opposite of 11 is 11, we write

0 11 0 11

c.0 225 0 means the opposite of the absolute value of 225. Since 0 225 0 225, and the opposite of 225 is 225, we write

0 225 0 225

The symbol is used to indicate a negative number, the opposite of a number, and the operation of subtraction. The key to reading the symbol correctly is to examine the context in which it is used.

Reading the Symbol

12	Negative twelve	A symbol directly in front of a number
		is read as “negative.”
		is read as “negative.”
	The opposite of	The ﬁrst symbol is read as “the opposite
( 12)	The opposite of	The ﬁrst symbol is read as “the opposite
	negative twelve	of” and the second as “negative.”
	negative twelve	of” and the second as “negative.”

12 5	Twelve minus ﬁve	Notice the space used before and after the
		symbol. This indicates subtraction and
		symbol. This indicates subtraction and
		is read as “minus.”

ANSWERS TO SELF CHECKS

2. a. b.

−4 −3 −2 −1 0 1 2 3 4

a. false b. true c. true d. false

4. a. 9 b. 4 5. a. 1 b. 4 c. 99

S E C T I O N 2.1 STUDY SET

VOCABULARY

Fill in the blanks.

1.numbers are greater than 0 and numbers are less than 0.

2.{ . . . , 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, . . . } is called


the set of		.
3. To	an integer means to locate it on the

number line and highlight it with a dot.

4.The symbols and are called symbols.

5. The of a number is the distance

between the number and 0 on the number line.

6.Two numbers that are the same distance from 0 on the number line, but on opposite sides of it, are called

CONCEPTS

7. Represent each of these situations using a signed number.

a. $225 overdrawn

b. 10 seconds before liftoff

c. 3 degrees below normal

d. A deﬁcit of $12,000

e. A 1-mile retreat by an army

8. Represent each of these situations using a signed number, and then describe its opposite in words.

a. A trade surplus of $3 million

b. A bacteria count 70 more than the standard

c. A proﬁt of $67

d. A business $1 million in the “black”

e. 20 units over their quota

9. Determine what is wrong with each number line.

a.
a.	−3	−2	−1	0	1	2 3		4
	−3	−2	−1	0	1	2 3		4
b.

	−3	−2	−1	0	2	4	6	8
	−3	−2	−1	0	2	4	6	8
c.

	−3	−2	−1	1	2	3	4	5
	−3	−2	−1	1	2	3	4	5
d.

	−3	−2	−1	0	1	2	3	4
	−3	−2	−1	0	1	2	3	4

2.1 An Introduction to the Integers	139

10.a. If a number is less than 0, what type of number must it be?

b.If a number is greater than 0, what type of number must it be?

11.On the number line, what number is

a.3 units to the right of 7?

b.4 units to the left of 2?

12.Name two numbers on the number line that are a distance of

a.5 away from 3.

b.4 away from 3.

13.a. Which number is closer to 3 on the number line: 2 or 7?

b.Which number is farther from 1 on the number line: 5 or 8?

14.Is there a number that is both greater than 10 and less than 10 at the same time?

15.a. Express the fact 12 15 using an symbol.

b.Express the fact 4 5 using an symbol.

16. Fill in the blank: The opposite of the		of a
number is that number.

17.Complete the table by ﬁnding the opposite and the absolute value of the given numbers.

Number Opposite Absolute value

18. Is the absolute value of a number always positive?

NOTATION

19.Translate each phrase to mathematical symbols.

a.The opposite of negative eight

b.The absolute value of negative eight

c.Eight minus eight

d.The opposite of the absolute value of negative eight

140	Chapter 2 The Integers

20.a. Write the set of integers.

b.Write the set of positive integers.

c.Write the set of negative integers.

21.Fill in the blanks.


a.	We read as “is		than or		to.”
b.	We read as “is	than or		to.”

22.Which of the following expressions contains a minus sign?

15 8 ( 15) 15

GUIDED PRACTICE

Graph the following numbers on a number line. See Example 1.

23. 3, 4, 3, 0, 1

−5 −4 −3 −2 −1 0 1 2 3 4 5

24. 2, 4, 5, 1, 1

−5 −4 −3 −2 −1 0 1 2 3 4 5

25. The integers that are less than 3 but greater than 5

−5 −4 −3 −2 −1 0 1 2 3 4 5

26. The integers that are less than 4 but greater than 3

−5 −4 −3 −2 −1 0 1 2 3 4 5

27.The opposite of 3, the opposite of 5, and the absolute value of 2

−5 −4 −3 −2 −1 0 1 2 3 4 5

28.The absolute value of 3, the opposite of 3, and the number that is 1 less than 3

−5 −4 −3 −2 −1 0 1 2 3 4 5

29.2 more than 0, 4 less than 0, 2 more than negative 5, and 5 less than 4

−5 −4 −3 −2 −1 0 1 2 3 4 5

30.4 less than 0, 1 more than 0, 2 less than 2, and 6 more than 4

−5 −4 −3 −2 −1 0 1 2 3 4 5

Place an or an symbol in the box to make a true statement.

See Example 2.

31.	5	5		32.	0	1
33.	12		6	34.	7		6

35.	10	17		36.	11	20
37.	325		532	38.	401		104

Tell whether each statement is true or false. See Example 3.


39.	15 14			40.	77 76
41.	210 210			42.	37 37
43.	1,255 1,254			44.	6,546 6,465
45.	0 8			46.	6 6
Find each absolute value. See Example 4.
47.	0	9 0		48.	0	12 0
49.	0	8 0		50.	0	1 0
51.	0	14 0		52.	0	85 0
53.	0	180 0		54.	0	371 0
Simplify each expression. See Example 5.
55.	( 11)			56.	( 1)
57.	( 4)			58.	( 9)
59.	( 102)			60.	( 295)
61.	( 561)			62.	( 703)
63.	0		20 0	64.	0		143 0
65.	0		6 0	66.	0		0 0
67.	0 253 0			68.	0		11 0
69.	0 0 0			70.	0		97 0

TRY IT YOURSELF

Place an or an symbol in the box to make a true statement.


71.	0 12 0		( 7)				72.	0 50 0		( 40)

73.	0	71 0		0		65 0	74.	0	163 0		0		150 0

75.	( 343)				( 161)		76.	( 999)				( 998)

77.	0	30 0		0		( 8) 0	78.	0	100 0		0		( 88) 0

Write the integers in order, from least to greatest.

79.82, 52, 52, 22, 12, 12

80.49, 9, 19, 39, 89, 49

Fill in the blanks to continue each pattern.

81.5, 3, 1, 1, , , , . . .

82.4, 2, 0, 2, , , , . . .

APPLICATIONS

83.HORSE RACING In the 1973 Belmont Stakes, Secretariat won by 31 lengths over second place ﬁnisher, Twice a Prince. Some experts call it the greatest performance by a thoroughbred in the

history of racing. Express the position of Twice a Prince compared to Secretariat as a signed number. (Source: ezinearticles.com)

84.NASCAR In the NASCAR driver standings, negative numbers are used to tell how many points behind the leader a given driver is. Jimmie Johnson was the leading driver in 2008. The other drivers in the top ten were Greg Bifﬂe ( 217), Clint Bowyer ( 303), Jeff Burton ( 349), Kyle Busch ( 498), Carl Edwards ( 69), Jeff Gordon ( 368), Denny Hamlin ( 470), Kevin Harvick ( 276), and Tony Stewart ( 482). Use this information to rank the drivers in the table below.

		AP Images
	2008 NASCAR Final Driver Standings

Rank	Driver	Points behind leader

1	Jimmie Johnson	Leader
2
3
4
5
6
7
8
9
10

(Source: NASCAR.com)

85.FREE FALL A boy launches a water balloon from the top of a building, as shown in the next column. At that instant, his friend starts a stopwatch and keeps track of the time as the balloon sails above

2.1 An Introduction to the Integers

141

the building and then falls to the ground. Use the number line to estimate the position of the balloon at each time listed in the table below.

		30
	1 sec	30
	1 sec	20


0 sec		10
	2 sec	10
	2 sec	0


		–10
		–10
		–20
		–20
		–30
		–30
	3 sec	–40
	3 sec	–40
		–50
		–50
		–60
		–60
		–70
		–70
		–80
		–80
		–90
		–90
		–100
		–100
		–110
	4 sec	–110
	4 sec	–120
		–120

Time	Position of balloon

0sec

1sec

2sec

3sec

4sec

86.CARNIVAL GAMES At a carnival shooting gallery, players aim at moving ducks. The path of one duck is shown, along with the time it takes the duck to reach certain positions on the gallery wall. Use the number line to estimate the position of the duck at each time listed in the table below.

0 sec	1 sec
	2 sec
3 sec	4 sec

−5 −4 −3 −2 −1 0 1 2 3 4 5

Time	Position of duck

0sec

1sec

2sec

3sec

4sec

142	Chapter 2 The Integers

87.TECHNOLOGY The readout from a testing device is shown. Use the number line to ﬁnd the height of each of the peaks and the depth of each of the valleys.

A peak

−1

−3

A valley

−5

88.FLOODING A week of daily reports listing the height of a river in comparison to ﬂood stage is given in the table. Complete the bar graph shown below.

Flood Stage Report

Sun.	2 ft below
Mon.	3 ft over
Tue.	4 ft over
Wed.	2 ft over
Thu.	1 ft below
Fri.	3 ft below
Sat.	4 ft below

Feet
4
3
2
1	Flood stage
0	Flood stage
−1
−2	Sun.
−3	Sun.
−4

89.GOLF In golf, par is the standard number of strokes considered necessary on a given hole. A score of 2 indicates that a golfer used 2 strokes less than par. A score of 2 means 2 more strokes than par were used. In the graph in the next column, each golf ball represents the score of a professional golfer on the 16th hole of a certain course.

a.What score was shot most often on this hole?

b.What was the best score on this hole?

c.Explain why this hole appears to be too easy for a professional golfer.

16th Hole

Meadow Pines

Golf Course

−3 −2 −1 Par 1	2	3
Under par	Over par

90.PAYCHECKS Examine the items listed on the following paycheck stub. Then write two columns on your paper—one headed “positive” and the other “negative.” List each item under the proper heading.

Tom Dryden Dec. 09		Christmas bonus	$100
Tom Dryden Dec. 09		Christmas bonus	$100

Gross pay	$2,000	Reductions
Overtime	$300	Retirement	$200
Deductions		Taxes
Union dues	$30	Federal withholding	$160
U.S. Bonds	$100	State withholding	$35

91.WEATHER MAPS The illustration shows the predicted Fahrenheit temperatures for a day in mid-January.

Seattle	−20°	0°
	−20°
	−10°
	−10°
Fargo		10°
	Chicago	New York
Denver		New York
Denver
San Diego		20°
		30°

Houston

40°

Miami

a.What is the temperature range for the region including Fargo, North Dakota?

b.According to the prediction, what is the warmest it should get in Houston?

c.According to this prediction, what is the coldest it should get in Seattle?

92.INTERNET COMPANIES The graph on the next page shows the net income of Amazon.com for the years 1998–2007. (Source: Morningstar)

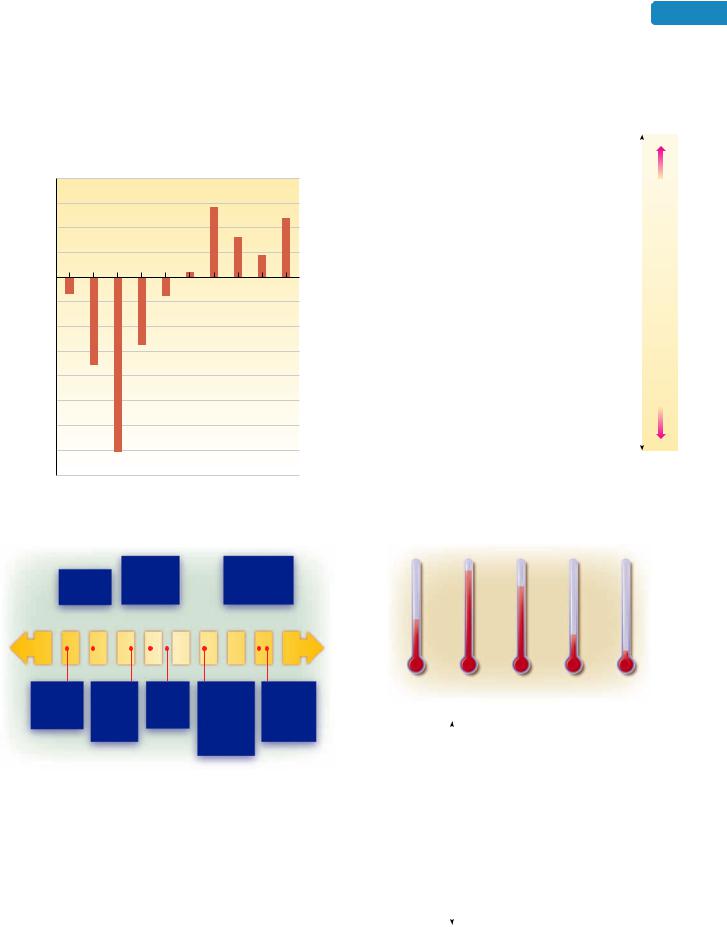
a.In what years did Amazon suffer a loss? Estimate each loss.

b.In what year did Amazon ﬁrst turn a proﬁt? Estimate it.

c.In what year did Amazon have the greatest proﬁt? Estimate it.

	800
	600
	400	Amazon.com
	400	Net Income
	200
	0	'98	'99	'00	'01	'02				Year
	0					'03	'04	'05	'06	Year
						'03	'04	'05	'06	'07
$ millions	–200
	–400
	–600
	–600
	–800
	–1,000
	–1,200
	–1,400
	–1,600

93.HISTORY Number lines can be used to display historical data. Some important world events are shown on the time line below.

				Romans				Muhammad
		Buddha		conquer				begins
		born 563		Greece 146			preaching 610
B.C.	800	600	400	200		200	400	600	800	A.D.
					0

First	Han	Jesus	Mayans	Ghana
Olympics	Dynasty	Christ	develop	empire
776	begins	born	advanced	flourishes
	202		civilization	mid-700s
			250

a.What basic unit is used to scale this time line?

b.What can be thought of as positive numbers?

c.What can be thought of as negative numbers?

d.What important event distinguishes the positive from the negative numbers?

94.ASTRONOMY Astronomers use an inverted vertical number line called the apparent magnitude

2.1 An Introduction to the Integers

143

scale to denote the brightness of objects in the sky. The brighter an object appears to an observer on Earth, the more negative is its apparent magnitude. Graph each of the following on

the scale to the right.

• Visual limit of binoculars 10			–25
• Visual limit of binoculars 10
• Visual limit of large telescope 20


•	Visual limit of naked eye 6		–20	ght
•	Visual limit of naked eye 6		–20
•	Full moon 12
•	Full moon 12		–15	Bri
•	Pluto 15


•	Sirius (a bright star) 2	ude	–10
•	Sirius (a bright star) 2		–10
•	Sun 26		–5
•	Venus 4	nit
•	Venus 4	mag
			0

		Apparent
		Apparent	5
			5
			10
			10
			15	Dim
			15
			20


			25
			25

95.LINE GRAPHS Each thermometer in the illustration gives the daily high temperature in degrees Fahrenheit. Use the data to complete the line graph below.

10°

5°

0°

−5°

−10°

−15°

Mon.

Tue.

Thu.

Fri.

Wed.

15°

Line graph

(Fahrenheit)

10°

5°

0°

Mon. Tue. Wed. Thu. Fri.

Temperatu

−5°

−10°

−15°

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 6712 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.12.2018408.58 Кб6antikrizisnoe-upravlenie.doc
#
18.12.2018108.03 Кб6ARHITYeKTURA.doc
#
10.06.20158.32 Mб301aswath_damodaran-investment_philosophies_2012.pdf
#
10.06.201582.94 Кб7audit_risk.doc
#
10.06.20154.17 Mб4BallotingApplicationDocs-SIMSUsersGuide.pdf
#
10.06.201515.55 Mб147basic mathematics for college students.pdf
#
10.06.2015901.06 Кб40Bazy_dannykh_i_znanii_UP_SHirokov_L.A._2000.pdf
#
29.03.20162.45 Mб35Bernd_Fon_Vittenburg_-_Shakh_planete_Zemlya.pdf
#
10.06.201561.93 Кб44bezopasnost.docx
#
10.06.20152.89 Mб84bibliofond_ru_604241.docx
#
10.06.20152.1 Mб30blind_watchmaker.pdf