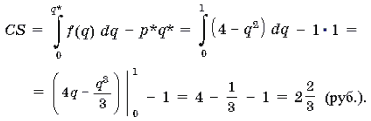- •Вопрос 11: Предел функции в точке и в бесконечности. Левый и правый предел функции.
- •Вопрос 12: Основные теоремы о пределах функции.
- •Вопрос 13: Замечательные пределы.
- •Вопрос 14: Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых функций.
- •Вопрос 15: Сравнение бесконечно больших функций. Связь между бесконечно малыми и бесконечно большими функциями.
- •Вопрос 16: Непрерывность функции в точке. Непрерывность сложной функции. Классификация точек разрыва.
- •Вопрос 17:Основные свойства непрерывной функции.
- •Вопрос 18: Понятие эмперической функции. Методы интерполяции и экстерполяции эмперической функции.
- •Вопрос 19:Функции в экономике. Функции предложения и спроса.
- •Вопрос 20:Производная. Геометрический и физический смысл производной.
- •Вопрос 21: Дифференцируемость функции в точке. Необходимые и достаточные условия дифференцируемости функции.
- •Вопрос 30: Основные теоремы дифференциального исчисления (теоремы Лангранджа о конечных приращениях, Коши)
- •Вопрос 31: Правило Лоппиталя. Нахождение пределов по правилу Лопитталя.
- •Вопрос 32:Условия возрастания и убывания функции.
- •Вопрос 33: Достаточное условие экстремума функции. Наибольшее и наименьшее значение функции.
- •Вопрос 34: Выпуклость функции и точка перегиба. Асимптоты графика функции.
- •Вопрос 35:Общая схема и следования функции и построения их графика.
- •Вопрос 36: Формула Тейлора. Остаточный член формулы Тейлора.
- •Вопрос 37: Формула Маклорена. Остаточный член формулы Маклорена.
- •Вопрос 39: Производные в экономических теориях. Дифференциальное исчисление при исследовании «эластичности» в экономике. Необходимое условие максимума прибыли.
- •Вопрос 40: Неопределённый интеграл. Первообразная.
- •Вопрос 41: Свойства неопределённого интеграла.
- •Вопрос 48: Интегрирование рациональных дробей.
- •Вопрос 49: Интегрирование иррациональных функций.
- •Вопрос 50: Интегрирование некоторых классов функций.
Вопрос 48: Интегрирование рациональных дробей.
Для
интегрирования рациональной функции
![]() ,
гдеP(x)
и Q(x)
- полиномы, используется следующая
последовательность шагов:
,
гдеP(x)
и Q(x)
- полиномы, используется следующая
последовательность шагов:
Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
Вычислить интегралы от простейших дробей.
Вопрос 49: Интегрирование иррациональных функций.
Основной приём решения иррациональных интегралов – это замена переменной, которая избавит нас от ВСЕХ корней в подынтегральной функции.
Для
интегрирования иррациональной функции,
содержащей
![]() используется
подстановка
используется
подстановка![]() .
Чтобы проинтегрировать иррациональную
функцию, содержащую несколько рациональных
степенейx, применяется подстановка
в форме
.
Чтобы проинтегрировать иррациональную
функцию, содержащую несколько рациональных
степенейx, применяется подстановка
в форме![]() ,
гдеnполагается равным наименьшему
общему кратному знаменателей всех
дробных степеней, входящих в данную
функцию.
Рациональная функцияxпод знаком корняn-ой степени, т.е.
выражение вида
,
гдеnполагается равным наименьшему
общему кратному знаменателей всех
дробных степеней, входящих в данную
функцию.
Рациональная функцияxпод знаком корняn-ой степени, т.е.
выражение вида![]() ,
интегрируется с помощью подстановки
,
интегрируется с помощью подстановки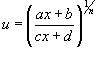 .
.
Вопрос 50: Интегрирование некоторых классов функций.
Рассмотрим
интегралы, подынтегральная функция в
которых содержит квадратный трёхчлен
![]() ,
где
,
где![]() --
некоторые постоянные, вида
--
некоторые постоянные, вида
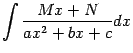 и
и 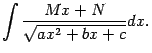
(Заметим,
что в числителе дроби должно стоять
линейное выражение
![]() ,
где
,
где![]() и
и![]() --
постоянные; при этом какой-либо из
постоянных не запрещается быть равной
0.)
--
постоянные; при этом какой-либо из
постоянных не запрещается быть равной
0.)
Такие интегралы приводятся к табличным следующим способом. Нужно выделить из квадратного трёхчлена выражение, равное полному квадрату, сделав такое преобразование:
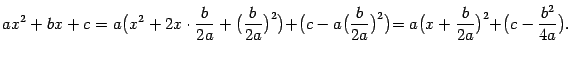
После
этого сделаем линейную замену
![]() и
получим интеграл одного из видов:
и
получим интеграл одного из видов:
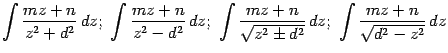
при
некоторых постоянных
![]() и
и![]() .
Далее разбиваем интеграл на два слагаемых
и в первом, в числителе подынтегральной
функции содержащем
.
Далее разбиваем интеграл на два слагаемых
и в первом, в числителе подынтегральной
функции содержащем![]() ,
делаем замену
,
делаем замену![]() ,
,![]() или
или![]() ,
согласно тому, что стоит в знаменателе.
После этого первое слагаемое приводится
к табличному интегралу. Второе слагаемое,
с
,
согласно тому, что стоит в знаменателе.
После этого первое слагаемое приводится
к табличному интегралу. Второе слагаемое,
с![]() в
числителе подынтегральной функции,
тоже даёт табличный интеграл.
в
числителе подынтегральной функции,
тоже даёт табличный интеграл.
Найдём интеграл
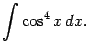
Подынтегральную функцию можно преобразовать, понизив степень:
|
|
|
|
|
|
Поэтому
|
|
|
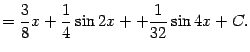
|
Вопрос 51: Определённый интеграл. Геометрический смысл определённого интеграла и его свойства.
51.1.
Приращение
первообразных функций F(x)+C
при переходе аргумента x
от значения x=a
к значению x=b,
равное разности F(b)-F(a),
называется определенным интегралом
и обозначается символом
51.2.Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, прилегающей к оси Ox и ограниченной кривой у=f(x) и прямыми у=0; х=а; х=b.
52.3.Величина
определенного интеграла не зависит
от обозначения переменной интегрирования,
т.е.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
V. Постоянный множитель можно выносить за знак определенного интеграла.
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
Вопрос 52: Теорема о среднем
Вопрос 53: Интеграл с переменным верхним пределом. Производная по переменному пределу интегрирования в определённом интеграле.
53.1.Пусть
на отрезке [ a,
b
] задана непрерывная функция f
( x
), тогда для любого
x
53.2.Если подынтегральная функция непрерывна,
топроизводнаяопределенного интеграла с переменным
верхним пределом существует и равна
значению подынтегральной функции для
этого предела. т.е.
Вопрос 54: Замена переменной в определённом интеграле. Пусть
функция φ(t) имеет непрерывную производную
на отрезке [α,β], а=φ(α), в=φ(β) и функция
f(х) непрерывна в каждой точке х вида
х=φ(t), где t Тогда
справедливо следующее равенство:
Вопрос 55: Несобственные интегралы. Определенный интеграл называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:
Вопрос 56: Приложения определённого интеграла. Вычисление плоских фигура и объёма тел вращения.
Площадь криволинейной трапеции, ограниченной неотрицательной функцией f (x), осью абсцисс и прямыми x = a, x = b, определяется как
Площадь криволинейного сектора равна
Требуется
найти объем тела вращения, образованного
вращением криволинейной трапеции
вокруг оси
Объем данного тела вычисляется по формуле, содержащей определенный интеграл:
Если
криволинейная трапеция прилежит к
оси
Вопрос 57:Вычисление длины дуги кривой.
Если
кривая задана уравнениями в
параметрической форме
Вопрос 58: Приложение определённого интеграла к задачам экономики. Выигрыш потребителя. Таким
образом, потребительский излишек
можно посчитать по следующей формуле Задача 1. Известно, что спрос на некоторый товар задается функцией p = 4 – q2, где q – количество товара (в шт.), p – цена единицы товара (в руб.), а равновесие на рынке данного товара достигается при p* = q* = 1. Определите величину потребитеоьского излишка Решение.
Вопрос 59: Приложение определённого интеграла к задачам экономики.Определение времени поставки товара и коэффициента Джина. Вопрос 60: Формула Ньютона – Лейбница.
|
|
|
|
|
|

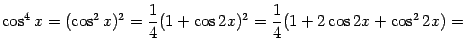
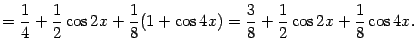
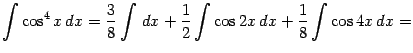
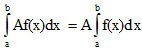
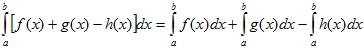

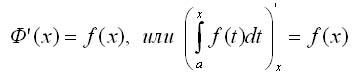
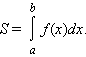
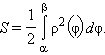
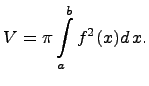
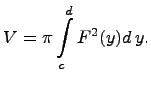
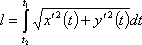 .где
.где