Вопрос 17:Основные свойства непрерывной функции.

17.1.Пусть функцияf: [a,b] →Rнепрерывна на сегменте [a,b], тогда:

1) она ограничена на этом сегменте;

2) если , то на сегменте [a,b] существуют точкиx₁иx₂такие, чтоf(x₁) =m,f(x₂) =M(теорема Вейерштрасса);

3) она принимает на каждом сегменте , все промежуточные значения междуf(α) иf(β) (теорема Коши).

Вопрос 18: Понятие эмперической функции. Методы интерполяции и экстерполяции эмперической функции.

18.1. Функция которая получена на основе проверенных данных, называется эмперической.

Такую функцию задают в виде таблицы или в виде графика

18.2. В тех случаях, когда необходимо определить опытным данным значение функции в точках не совпадающих с опытным данными, применяется метод интерполяции.

Если необходимо определить значение функции за пределом опытных данных то применяется метод эктерполяции. Линейная интерполяция основана на понятие уравнения линии проходящей через две заданные точки.

Вопрос 19:Функции в экономике. Функции предложения и спроса.

19.1 Наиболее часто используют в экономике следующие функции:

1. Функция полезности (функция предпочтения).

2. Производственная функция.

3. Функция выпуска

4.Функция издержек

5. Функция спроса, потребления и предложения.

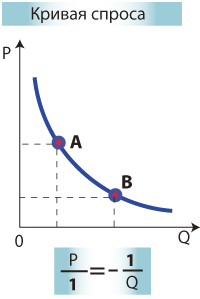
19.2.-Функция спроса

где Q - величина спроса или величины приобретаемого товара;

Р – цена.

f - показатель функциональной зависимости величины спроса от цены

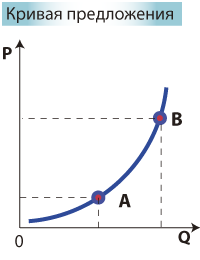
  Qs = f(P) – Функция предложения

где Qs - величина предложения или объем продаваемого товара; Р - цена.

Вопрос 20:Производная. Геометрический и физический смысл производной.

20.1. Производной функции y = f(x) называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.

20.2. Производная f'(x) есть угловой коэффициент (тангенс угла наклона) касательной, проведённой к кривой у=f(x) в точке х₀. т.е. k= f'(x₀) – геометрический смысл производной.

Производная пути по времени S'(t₀) есть скорость точки в момент t₀ : v(t₀) = s'(t₀) – физический смысл производной.

Вопрос 21: Дифференцируемость функции в точке. Необходимые и достаточные условия дифференцируемости функции.

21.1. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке.

21.2. Для того, чтобы функцияf(x) была дифференцируема в точкеx0, необходимо и достаточно, чтобы в этой точке она имела конечную производную. При этом Δf=f'(x0) · Δx+o(Δx),.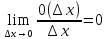

Вопрос 22:Связь между дифференцируемостью и непрерывностью функции.

22.1. Если функция у =f(x) дифференцируема в точкеx_0, то она в этой точке непрерывна.

Непрерывность функции необходимое, но не достаточное условие дифференцируемости функции.

Вопрос 23:Дифференцирование суммы, произведения и частного.

23.1.

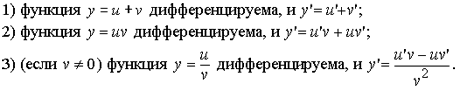
Вопрос 24: Дифференциал функции. Приближенное вычисление с помощью дифференциалов.

24.1. Дифференциалом функцииу=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

dy=ƒ'(х)•∆

24.2.

Эту формулу можно применять для приближённого вычисления значений функции в точках, если известны значенияи её частных производныхв точке.

Вопрос 25: Производная обратной и сложной функции. Производные обратных тригонометрических функций.

25.1. Если функцииy = y(u),u = u(x)дифференцируемы (т.е. существуют производныеy'_u,u'_x), тогда сложная функцияy = y(u(x))дифференцируема иy'_x = y'_u u'_x.

Если обратная функция x = g(y)дифференцируема иg'(y) ≠ 0, то функцияy=f(x)дифференцируема, и

25.2. ;;

;;;;

;

Вопрос 26: Производные основных элементарных функций. Таблица производных.

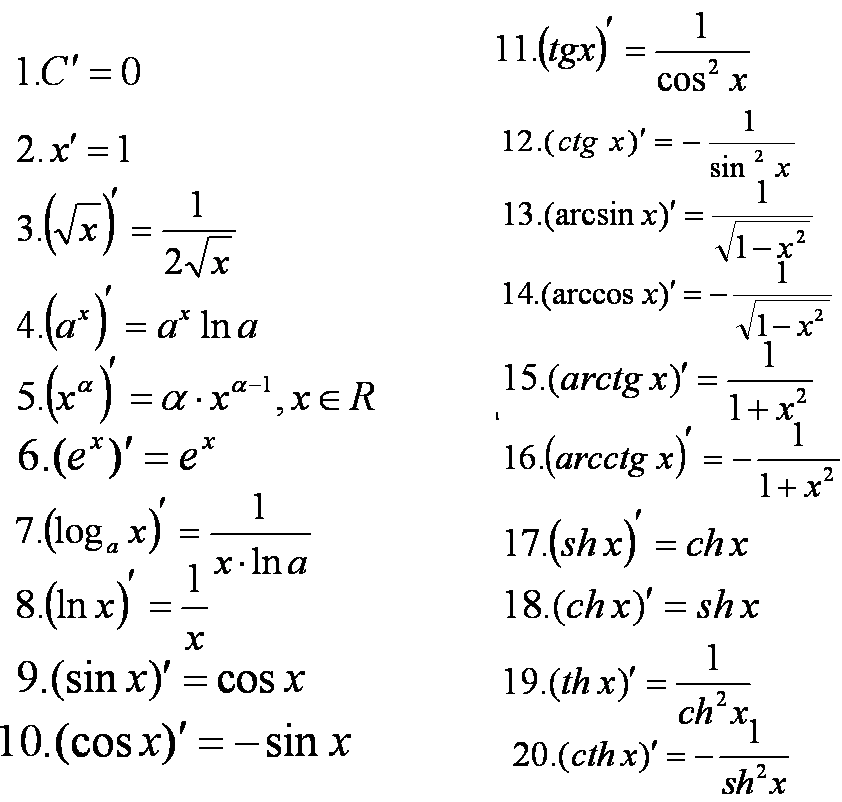
Вопрос 27: Дифференцирование функцию заданной параметрически. Производная неявной функции.

27.1.Если функция f задана параметрически x = φ(t), y = ψ(t), α < t < β,

где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то

27.2. Еслиy=f(x) - дифференцируемая функция, заданная уравнениемF(x,y) = 0, т. е.F(x,f(x))≡ 0 на некотором интервале ]a,b[, то во многих случаях ее производную можно найти из уравнения

Вопрос 28: Производные высших порядков. Дифференциалы высших порядков.

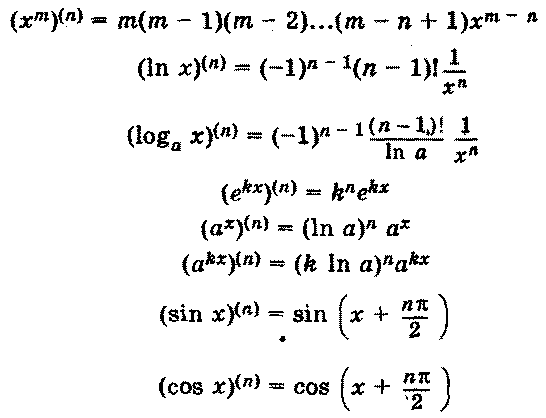
Вопрос 29:Основные теоремы дифференциального исчисления (Теоремы Ферма, Ролля)

Теорема Ферма Пусть функция y=f(x), непрерывная в некотором замкнутом интервале [x₁, x₂] принимает свое наибольшее (или наименьшее) значение во внутренней точке (кси) этого интервала: x_{1 <} (кси) < x₂ Если в точке (кси) производная функции f(x) существует, то она обязательно равна нулю: f′(x)=0

Теорема Ролля. Если функция f(x) непрерывна на замкнутом интервале [а, b], имеет внутри интервала производную и если f(a) = f(b), то внутри интервала [а, b] найдется хотя бы одно такое значение x₀ (a < x₀ < b), что f ' (x₀) = 0.